Matemática

O triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou matemáticos desde a Antiguidade. Triângulo retângulo é aquele que apresenta um ângulo interno medindo 90o. Esse tipo de triângulo apresenta propriedades e características muito relevantes. Faremos o estudo das relações entre as medidas dos lados do triângulo retângulo.
Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.
Observe a figura abaixo.
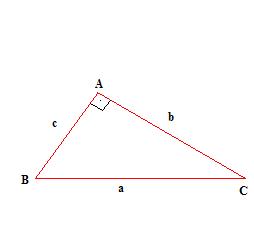
Temos que:
a → é a hipotenusa
b e c → são os catetos.
A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.
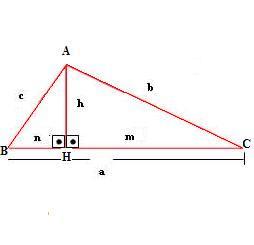
BH = n e CH = m são as projeções dos catetos sobre a hipotenusa.
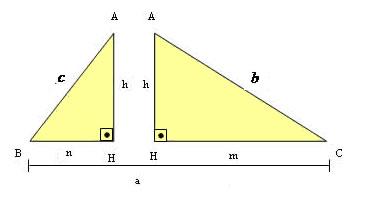
Os três triângulos são semelhantes
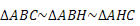
Da semelhança de triângulos obtemos as seguintes relações:
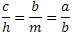
Daí segue que:
b2 = am e ah = bc
Temos, também, as seguintes relações:
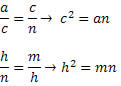
E a mais famosa das relações métricas no triângulo retângulo:
a2 = b2 + c2
Que é o teorema de Pitágoras.
Observe que temos cinco relações métricas no triângulo retângulo:
1. b2 = am
2. ah = bc
3. c2 = an
4. h2 = mn
5. a2 = b2 + c2
Todas elas são de grande utilidade na resolução de problemas que envolvem triângulos retângulos.
Exemplo. Determine as medidas da altura relativa à hipotenusa e dos dois catetos do triângulo abaixo.
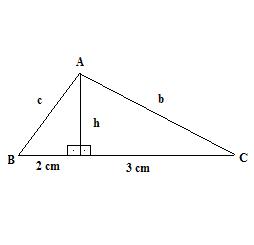
Solução: Temos que
n = 2 cm
m = 3 cm
Utilizando a quarta relação descrita anteriormente, obtemos:
h2 = mn
h2 = 3∙2
h2 = 6
h = √6
Segue que:
a = 2 + 3 = 5 cm
Daí, utilizando a primeira relação, obtemos:
b2 = am
b2 = 5∙3
b2 = 15
b = √15
Da terceira relação, obtemos:
c2 = an
c2 = 5∙2
c2 = 10
c = √10
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Trigonometria No Triângulo Retângulo
Trigonometria no Triângulo Retângulo Marcos Noé Relações trigonométricas no triângulo retânguloA trigonometria surgiu diante da necessidade do homem de calcular medidas com base em ângulos. Os estudos relacionados aos triângulos...
- Relações Métricas Triângulo Retângulo
Triângulo retângulo Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo...
- Relações Métricas Triângulo Retângulo
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que:...
- Triângulo Retângulo Exercícios
c² = a.n b² = a.m h² = m.n c.b = a.h c² + b² = a² Exercícios sobre Relações Métricas no Triângulo Retângulo. 1. Em um triângulo retângulo as projeções dos catetos sobre a hipotenusa medem 6 cm e 8 cm. Determine a altura relativa à hipotenusa...
Matemática
Relações métricas no triângulo retângulo
Relações métricas no triângulo retângulo
Marcelo Rigonatto
Triângulo retângulo
Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.
Observe a figura abaixo.
Temos que:
a → é a hipotenusa
b e c → são os catetos.
A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.
BH = n e CH = m são as projeções dos catetos sobre a hipotenusa.

Os três triângulos são semelhantes
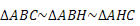
Da semelhança de triângulos obtemos as seguintes relações:
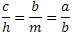
Daí segue que:
b2 = am e ah = bc
Temos, também, as seguintes relações:
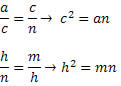
E a mais famosa das relações métricas no triângulo retângulo:
a2 = b2 + c2
Que é o teorema de Pitágoras.
Observe que temos cinco relações métricas no triângulo retângulo:
1. b2 = am
2. ah = bc
3. c2 = an
4. h2 = mn
5. a2 = b2 + c2
Todas elas são de grande utilidade na resolução de problemas que envolvem triângulos retângulos.
Exemplo. Determine as medidas da altura relativa à hipotenusa e dos dois catetos do triângulo abaixo.
Solução: Temos que
n = 2 cm
m = 3 cm
Utilizando a quarta relação descrita anteriormente, obtemos:
h2 = mn
h2 = 3∙2
h2 = 6
h = √6
Segue que:
a = 2 + 3 = 5 cm
Daí, utilizando a primeira relação, obtemos:
b2 = am
b2 = 5∙3
b2 = 15
b = √15
Da terceira relação, obtemos:
c2 = an
c2 = 5∙2
c2 = 10
c = √10
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Trigonometria No Triângulo Retângulo
Trigonometria no Triângulo Retângulo Marcos Noé Relações trigonométricas no triângulo retânguloA trigonometria surgiu diante da necessidade do homem de calcular medidas com base em ângulos. Os estudos relacionados aos triângulos...
- Relações Métricas Triângulo Retângulo
Triângulo retângulo Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo...
- Relações Métricas Triângulo Retângulo
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que:...
- Triângulo Retângulo Exercícios
c² = a.n b² = a.m h² = m.n c.b = a.h c² + b² = a² Exercícios sobre Relações Métricas no Triângulo Retângulo. 1. Em um triângulo retângulo as projeções dos catetos sobre a hipotenusa medem 6 cm e 8 cm. Determine a altura relativa à hipotenusa...
