Matemática

Exemplos:
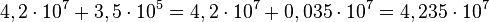
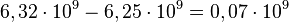 (não padronizado) ou
(não padronizado) ou 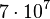 (padronizado)
(padronizado)
Exemplos:
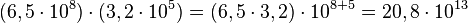 (não padronizado)
(não padronizado) 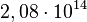 (convertido para a notação padronizada)
(convertido para a notação padronizada)
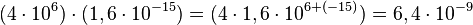 (já padronizado sem necessidade de conversão)
(já padronizado sem necessidade de conversão)
Exemplos:
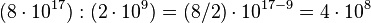 (padronizado)
(padronizado)
 (não padronizado)
(não padronizado) 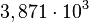
 (padronizado)
(padronizado)

![\sqrt[5]{6,7\cdot 10^{17}} = \sqrt[5]{670\cdot 10^{15}} = \sqrt[5]{670}\cdot 10^{15/5} \approx 3,674\cdot 10^{3}](matematica/matematica-5631d1f2066cd.png)
- Expressão Numérica C/ Potencia E Raiz
POTENCIAÇÃO E RADICIAÇÃO POTENCIAÇÃO Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes...
- Potenciação E Radiciação
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- SimplificaÇÃo De Radicais
Simplificar um radical significa escrevê-lo sob a forma mais simplis e equivalentes ao radical dado 1º) CASO: O índice e o expoente do radicando são divisíveis por um mesmo número (diferente de zero) Exemplos a) ¹²√3¹⁰ = ¹²⁾²√3¹⁰⁾²...
- Potenciação: Definição E Exemplos
PotênciaPodemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 26, onde 2 é a base e 6 o expoente (Leia: dois elevado...
Matemática
Operações com Notação Científica

Adição e Subtração
Para somar ou subtrair dois números em notação científica, é necessário que os expoentes sejam o mesmo. Ou seja, um dos valores deve ser transformado para que seu expoente seja igual ao do outro. A transformação segue o mesmo princípio de equilíbrio. O resultado possivelmente não estará na forma padronizada, sendo convertido posteriormente.
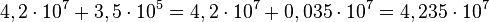
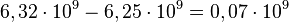 (não padronizado) ou
(não padronizado) ou 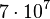 (padronizado)
(padronizado)Multiplicação
Multiplicamos as mantissas e somamos os expoentes de cada valor. O resultado possivelmente não será padronizado, mas pode ser convertido.
Exemplos:
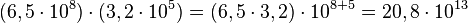 (não padronizado)
(não padronizado) 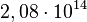 (convertido para a notação padronizada)
(convertido para a notação padronizada)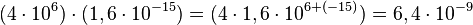 (já padronizado sem necessidade de conversão)
(já padronizado sem necessidade de conversão)Divisão
Dividimos as mantissas e subtraímos os expoentes de cada valor. O resultado possivelmente não será padronizado, mas pode ser convertido:
Exemplos:
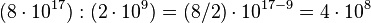 (padronizado)
(padronizado) (não padronizado)
(não padronizado) 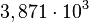
Exponenciação
A mantissa é elevada ao expoente externo e o congruente da base dez é multiplicado pelo expoente externo. (padronizado)
(padronizado)Radiciação
Antes de fazer a radiciação é preciso transformar um expoente para um valor múltiplo do índice. Após feito isso, o resultado é a radiciação da mantissa multiplicada por dez elevado à razão entre o expoente e o índice do radical.

![\sqrt[5]{6,7\cdot 10^{17}} = \sqrt[5]{670\cdot 10^{15}} = \sqrt[5]{670}\cdot 10^{15/5} \approx 3,674\cdot 10^{3}](matematica/matematica-5631d1f2066cd.png)
Referências
Profº Luiz Claudio. http://luizclaudionovaes.sites.uol.com.br/notacao.htm
- Expressão Numérica C/ Potencia E Raiz
POTENCIAÇÃO E RADICIAÇÃO POTENCIAÇÃO Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes...
- Potenciação E Radiciação
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- SimplificaÇÃo De Radicais
Simplificar um radical significa escrevê-lo sob a forma mais simplis e equivalentes ao radical dado 1º) CASO: O índice e o expoente do radicando são divisíveis por um mesmo número (diferente de zero) Exemplos a) ¹²√3¹⁰ = ¹²⁾²√3¹⁰⁾²...
- Potenciação: Definição E Exemplos
PotênciaPodemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 26, onde 2 é a base e 6 o expoente (Leia: dois elevado...
