Matemática

Por que "menos vezes menos dá mais"?

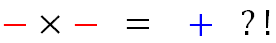As pessoas sabem desde muito cedo (talvez desde o fundamental) que as regras de sinais para a multiplicação podem ser representadas por algo como uma tabelinha:

+ + = +

- - = +

+ - = -

- + = -

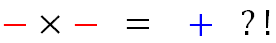
Se alguma das regras acima pode causar perplexidade é a segunda: que menos vezes menos dá mais, pois ela não é (ao menos não para mim) tão intuitiva.

Esta postagem se dedica então a demonstrá-la.

É claro que ninguém duvida da veracidade desta regra , afinal certamente elas nunca falharam, mas não é difícil encontrar um indivíduo que não sabe de onde é que ela saiu (ainda que ele a use todo dia!).

Para responder de forma simples a pergunta porque "menos vezes menos dá mais"? poderíamos simplesmente dizer que é uma consequência lógica de alguns axiomas.

Mas dizer apenas isto é muito pouco instrutivo e não satisfaz a ninguém. Vamos então para uma demonstração:

Para mostrar que, de fato, menos vezes menos dá mais precisamos admitir alguns fatos relacionados aos números reais. Vamos chamá-los de axiomas e simplesmente aceitá-los como sendo válidos:

Observação: Todas as letras em negrito abaixo (x, y, z, a e b) representam números reais.

1º axioma: a igualdade é reflexiva, ou seja, todo valor é igual a si próprio:

x = x

2º axioma: se a dois valores iguais somarmos um terceiro valor os resultados serão iguais, ou seja:

Se x = y, então x + z = y + z

3º axioma: a operação de adição é associativa, isto significa que o modo como os parênteses são arranjados é totalmente desimportante:

x + (y + z) = (x + y) + z

4º axioma: todo número x tem um simétrico que é denotado por -x. Quando somamos um número ao seu simétrico obtemos zero:

x + (-x) = 0

5º axioma: o número zero é o elemento nulo da adição, ou seja:

x + 0 = x

6º axioma: a operação de adição é comutativa, ou seja, a ordem das parcelas não altera a soma:

x + y = y + x

7º axioma: a igualdade é simétrica, ou seja:

Se x = y, então y = x

8º axioma: vale a lei distributiva, ou seja:

x(y + z) = xy + xz
(y + z)x = yx + zx

Até aqui tudo bem, certo? Mas veja que interessante: aceitando estes axiomas obtemos algumas consequências bem legais:

Consequência [i]:

Se x + y = x, então y = 0

Veja porque isso é verdade:

Supõe que

x + y = x

Como (-x) = (-x), podemos utilizar o 2º axioma e escrever:

(-x) + (x + y) = (-x) + x

Devido ao fato de a adição ser associativa obtemos:

((-x) + x) + y = (-x) + x

Mas a soma de um elemento com seu simétrico resulta em zero, ou equivalentemente, devido à comutatividade da adição, a soma do simétrico com o elementos resulta em zero, portanto temos:

0 + y = 0

Mas o zero é o elemento nulo da adição:

y = 0

Assim fica demonstrada a consequência [i]. Vejamos mais uma consequência:

Consequência [ii]:

0x = 0

Vamos explicá-la: começamos utilizando a reflexividade:

0x = 0x

O quinto axioma nos diz que 0 = 0 + 0 (basta por o zero no lugar do x) então podemos escrever:

0x = (0 + 0)x

Pela Lei Distributiva:

0x = 0x + 0x

Como a igualdade é simétrica:

0x + 0x = 0x

Agora, usando a consequência [i] concluímos o que queríamos:

0x = 0

Observe que a consequência [i] nos diz que se somarmos dois números e o resultado obtido for igual a um dos números somados, então o outro número é necessariamente o zero. Vamos explicar melhor:

A consequência anterior nos diz que se x + y = x, então y = 0. No nosso caso tínhamos 0x + 0x = 0x, donde resulta que 0x = 0.

Vamos ver mais uma consequência:

Consequência [iii]:

-xy = (-x)y

Prova:

Pela lei distributiva podemos escrever:

xy + (-x)y = (x + (-x))y

Pelo axioma do simétrico (no segundo membro da igualdade) obtemos:

xy + (-x)y = 0y

Como o produto de zero por qualquer número é zero (devido a consequência [ii]):

xy + (-x)y = 0

Como a soma acima resulta em zero o elemento (-x)y deve ser o simétrico do elemento xy, ou seja:

(-x)y = -xy

(Observe que o que acaba de ser feito é a demonstração de que menos vezes mais dá menos).
Do mesmo modo é possível mostrar que x(-y) = -xy. O leitor que compreendeu a demonstração acima é capaz de construir esta.

Vamos então a consequência que, neste texto, sucede a demonstração de que menos vezes menos dá mais:

Consequência [iv]:

x = -(-x)

Veja o motivo:

Pelo axioma do elemento simétrico:

x + (-x) = 0

Pela comutatividade da adição:

(-x) + x = 0

Logo x deve ser o simético de (-x) ou seja:

x = -(-x)

Todos estas consequências são necessárias para o propósito desta postagem: demonstrar que menos com menos dá mais. Na verdade para este fim precisamos diretamente apenas das consequências [iii] e [iv], contudo a consequência [iii] exige a consequência [ii] que por sua vez exige a consequência [i]. Este é o motivo de termos demonstrado todas elas.

E as quatro consequências apresentadas dependem vitalmente dos oito axiomas enunciados no início.

Vamos enfim provar que:

(-a)(-b) = ab

Temos pela reflexividade que:

(-a)(-b) = (-a)(-b)

Fazendo uso da consequência [iii] podemos escrever:

(-a)(-b) = -(a(-b))

E novamente pela mesma consequência (pela parte que ficou para o leitor demonstrar), obtemos:

(-a)(-b) = -(-ab)

E finalmente, pela consequência [iv]:

(-a)(-b) = ab

E é isto que queríamos demonstrar.

Observação: Há outras maneiras de demonstrar que menos vezes menos dá mais. Talvez, e só talvez, faremos isso em postagens futuras aqui no BLOG MANTHANO, apresentando inclusive argumentos mais simples que podem ser trabalhados no ensino fundamental. Contudo estes últimos o leitor poderá encontrar na última referência (que foi inclusa só para este fim e está disponível para download em sites de compartilhamento de arquivos).

Vale salientar que enunciamos apenas os axiomas necessários e suficientes para demonstrar o que queríamos, de modo que há outros axiomas e muitas outras consequências que sequer foram mencionadas. Este conteúdo pode, sem dúvidas, ser encontrado em livros de álgebra abstrata.

Referências:

NACHBIN, Leopoldo. Introdução à Álgebra. Rio de Janeiro, Editora McGraw-Hill do Brasil, Ltda. 1971.

LIMA, Elon Lages. Conceitos e Controvérsias. In: Meu Professor de matemática e Outras Histórias, Sociedade Brasileira de Matemática, 1991, p. 149-206.

*Erros podem ser apontados aqui.

_______________________________________________________

FIQUE SABENDO OUTROS PORQUÊS:

Por que todo número elevado a zero dá um?

Por que racionalizar o denominador?

_______________________________________________________

- Algumas Curiosidades Lógicas
Nesta postagem não há tema novo algum. Tudo aqui se refere a assuntos muito conhecidos na literatura especializada. No entanto, como vejo inúmeros discursos e textos de matemática no Brasil que fazem consideráveis confusões de caráter lógico,...

- A Demonstração Por Indução
Esta postagem é a segunda da série sobre os números naturais. Na primeira enunciamos os chamados Axiomas de Peano e nesta vamos volver nossa atenção para o quinto deles, chamado o Princípio da Indução: Se X ? ? é tal que 1 ? X e, para todo...

- Os Axiomas De Peano
Esta postagem (cuja intenção é enunciar os Axiomas de Peano) dá início a uma série que tem o objetivo de tratar sobre alguns aspectos dos números naturais. Notemos, inicialmente, que a utilidade dos Axiomas de Peano não é definir, mas...

- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...

- O Porquê Dos Complexos Não Ser Um Corpo Ordenado
Quem é maior, ou ? Se você já se fez essa pergunta, com certeza se indagou motivo de não saber respondê-la, o motivo disso é o fato de que o corpo dos complexos não pode ser ordenado. Mas afinal, o que quer dizer um corpo ser "ordenado"?...

Matemática