Representamos por an, a potência de base real a e expoente inteiro n.
Definimos a potência an nos casos abaixo:
• 1º caso: Expoente inteiro maior que 1.
• 1º caso: Expoente inteiro maior que 1.
Potência de expoente inteiro maior que 1 é o produto de tantos fatores iguais à base quantas forem as unidades do expoente.
Assim:

Exemplos:
a) 43 = 4 · 4 · 4 = 64
b) 15 = 1 · 1 · 1 · 1 · 1 = 1
c) (–2)4= (–2) · (–2) · (–2) · (–2) = 16
d) 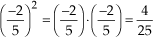
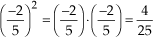
• 2º caso: Expoente 1
Toda potência de expoente 1 é igual à base.
Assim:

Exemplos
a) 51 = 5
b) 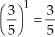
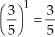
• 3º caso: Expoente zero
Toda potência de expoente zero é igual a 1.
Assim:

Exemplos
a) 50 = 1
b) 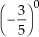 = 1
= 1
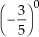 = 1
= 1 • 4º caso: Expoente inteiro negativo
Toda potência de expoente inteiro negativo e base não-nula é igual à potência de base igual ao inverso da base dada e expoente igual ao oposto do expoente dado.
Assim:
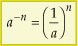
Exemplos:
a) 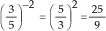
b)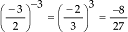
c)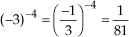
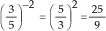
b)
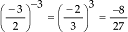
c)
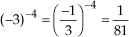
Observação:
Sendo n um número inteiro, temos:
1a) a = 0 e n > 0
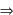 an = 0
an = 02a) a = 0 e n < 0
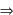
 an
an 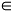 R
R3a) a > 0
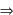 an > 0
an > 04a) a < 0 e n par
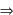 an > 0
an > 05a) a < 0 e n ímpar
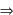 an < 0
an < 0 2. Propriedades
Consideremos os números reais a e b, e os números naturais m e n. Então são válidas as seguintes propriedades.
• P1: Produto de potências de mesma base
Para multiplicarmos potências de mesma base, conservamos a base e somamos os expoentes.

Justificativa:
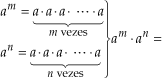
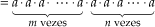 =
= 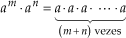
Assim: am · an = am+n.
Exemplos:
a) 23 · 25 = 23+5 = 28
b) 4x · 4-x+2 = 4x+(-x+2) = 42
c) 3 · 32 · 36 = 31+2+6 = 39
• P2: Quociente de potências de mesma base
Para dividirmos potências de mesma base, conservamos a base e subtraímos os expoentes.
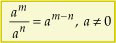
Justificativa:
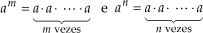
1o. Sendo m > n, temos
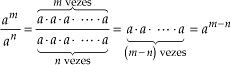
2o. Se m = n, 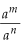 = 1= a(m-n) = a0 = 1
= 1= a(m-n) = a0 = 1
3o. Se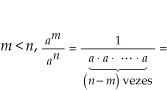
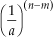 = a (m - n)
= a (m - n)
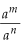 = 1= a(m-n) = a0 = 1
= 1= a(m-n) = a0 = 13o. Se
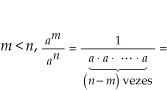
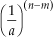 = a (m - n)
= a (m - n) Exemplos:
a) 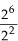 = 26-2 = 24
= 26-2 = 24
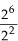 = 26-2 = 24
= 26-2 = 24 b) 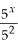 = 5x-2
= 5x-2
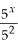 = 5x-2
= 5x-2 c) 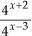 = 4(x+2)-(x-3) = 45
= 4(x+2)-(x-3) = 45
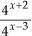 = 4(x+2)-(x-3) = 45
= 4(x+2)-(x-3) = 45 • P3: Produto de potências de mesmo expoente
Para multiplicarmos potências de mesmo expoente, conservamos o expoente e multiplicamos as bases.

Justificativa
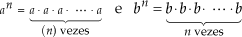
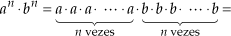
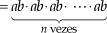
Assim: an · bn = (ab)n.
Exemplos
a) 24 · 84 = (2 · 8)4 = 164
b) x3 · y3 · z3 = (x · y · z)3
• P4: Quociente de potências de mesmo expoente
Para dividirmos potências de mesmo expoente, conservamos o expoente e dividimos as bases.
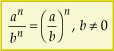
Justificativa:
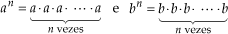
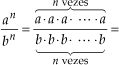
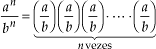
Assim:
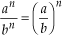
Exemplos:
a)
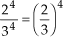
b)
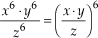
• P5: Potência de uma potência
Para elevarmos uma potência a um novo expoente, conservamos a base e multiplicamos os expoentes.

Justificativa:
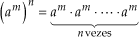
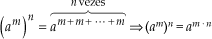
Exemplos:
a) (23)2 = 22.2 = 26
b)
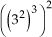 = 32.3.2 = 312
= 32.3.2 = 312Observação
As propriedades apresentadas podem ser estendidas para os expoentes m e n inteiros.
Exemplos
a) 23 · 2-2 = 23 + (-2) = 21 (P1)
b)
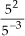 = 52 - (-3) = 52 + 3 = 55 (P2)
= 52 - (-3) = 52 + 3 = 55 (P2)c) 5-3 · 2-3 = (5 · 2)-3 = 10-3 (P3)
d)
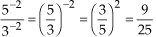 (P4)
(P4)e)
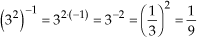 (P5)
(P5)Situações Especieais
A. (– a)n e –an
As potências (–a)n e –an , em geral, apresentam resultados diferentes, pois:
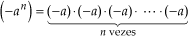
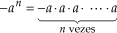
Exemplos
a) (–2)4 = (–2) · (–2) · (–2) · (–2) = 16
b) –24 = – 2 · 2 · 2 · 2 = –16
c) (–2)3 = (–2) · (–2) · (–2) = –8
d) –23 = – 2 · 2 · 2 = –8
B.
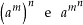
As potências
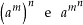 , em geral, apresentam resultados diferentes, pois:
, em geral, apresentam resultados diferentes, pois: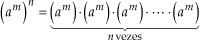
e
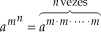
Exemplos
a)
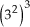 = (32) · (32) · (32) = 32 · 3 = 36
= (32) · (32) · (32) = 32 · 3 = 36b)
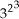 = 32 · 2 · 2 = 38
= 32 · 2 · 2 = 38 