Matemática
• 2º caso: Expoente 1
• 3º caso: Expoente zero
• 4º caso: Expoente inteiro negativo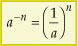
Observação:
1a) a = 0 e n > 0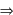
an = 0
2a) a = 0 e n < src="matematica/matematica-57ac25eceb6fd.gif" alt="seta" >
an 
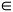R
3a) a > 0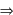 an > 0
4a) a <>n par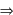 an > 0
5a) a <>n ímpar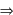 an <>
2. Propriedades
• P1: Produto de potências de mesma base
= 
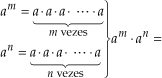
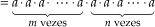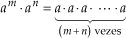
Assim: am · an = am+n.
• P2: Quociente de potências de mesma base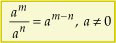
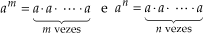
1o. Sendo m > n, temos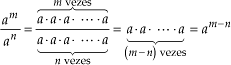
Exemplos:
• P3: Produto de potências de mesmo expoente
Justificativa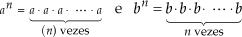
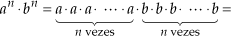
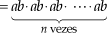
Assim: an · bn = (ab)n.
Exemplos
a) 24 · 84 = (2 · 8)4 = 164
b) x3 · y3 · z3 = (x · y · z)3
• P4: Quociente de potências de mesmo expoente
Para dividirmos potências de mesmo expoente, conservamos o expoente e dividimos as bases.
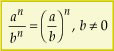
Justificativa:
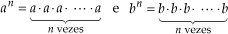
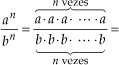
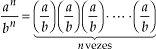
Assim:
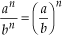
Exemplos:
a)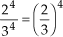
b)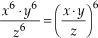
• P5: Potência de uma potência
Para elevarmos uma potência a um novo expoente, conservamos a base e multiplicamos os expoentes.
Justificativa:
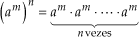
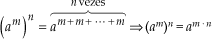
Exemplos:
a) (23)2 = 22.2 = 26
b)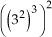
= 32.3.2 = 312
Observação
As propriedades apresentadas podem ser estendidas para os expoentes m e n inteiros.
Exemplos
a) 23 · 2-2 = 23 + (-2) = 21 (P1)
b)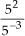
= 52 - (-3) = 52 + 3 = 55 (P2)
c) 5-3 · 2-3 = (5 · 2)-3 = 10-3 (P3)
d)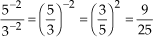
(P4)
e)
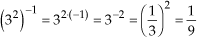(P5)
Situações Especieais
A. (– a)n e –an
As potências (–a)n e –an , em geral, apresentam resultados diferentes, pois:
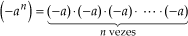
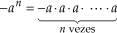
Exemplos
a) (–2)4 = (–2) · (–2) · (–2) · (–2) = 16
b) –24 = – 2 · 2 · 2 · 2 = –16
c) (–2)3 = (–2) · (–2) · (–2) = –8
d) –23 = – 2 · 2 · 2 = –8
B.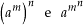
As potências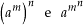, em geral, apresentam resultados diferentes, pois:
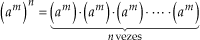
e
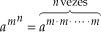
Exemplos
a)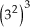
= (32) · (32) · (32) = 32 · 3 = 36
b)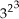
= 32 · 2 · 2 = 38
- Jura? Outra Forma De Calcular Potências Com Expoente 2
Olá pessoal, Normalmente, aprendemos no ensino fundamental como calcular potências. Vamos relembrar? Definição: Dado um certo número real qualquer (i), e um número n, inteiro e positivo, é definido in = potência de base (i) com expoente...
- Expressão Numérica C/ Potencia E Raiz
POTENCIAÇÃO E RADICIAÇÃO POTENCIAÇÃO Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes...
- Potenciação E Radiciação
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Potenciação
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br Representamos por an, a potência de base real a e expoente inteiro n....
Matemática
Potenciação
Representamos por an, a potência de base real a e expoente inteiro n.
Definimos a potência an nos casos abaixo:
• 1º caso: Expoente inteiro maior que 1.
• 1º caso: Expoente inteiro maior que 1.
Potência de expoente inteiro maior que 1 é o produto de tantos fatores iguais à base quantas forem as unidades do expoente.
Assim:
Exemplos:
a) 43 = 4 · 4 · 4 = 64
b) 15 = 1 · 1 · 1 · 1 · 1 = 1
c) (–2)4= (–2) · (–2) · (–2) · (–2) = 16
d)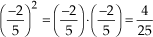 
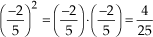
• 2º caso: Expoente 1
Toda potência de expoente 1 é igual à base.
Assim:
Exemplos
a) 51 = 5
b)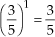 
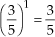
• 3º caso: Expoente zero
Toda potência de expoente zero é igual a 1.
Assim:
Exemplos
a) 50 = 1
b)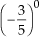 
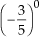= 1
= 1 • 4º caso: Expoente inteiro negativo
Toda potência de expoente inteiro negativo e base não-nula é igual à potência de base igual ao inverso da base dada e expoente igual ao oposto do expoente dado.
Assim:
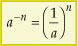
Exemplos:
a)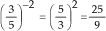 
b)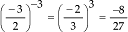
c)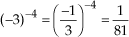
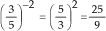
b)
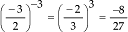
c)
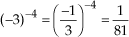
Observação:
Sendo n um número inteiro, temos:
1a) a = 0 e n > 0
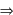an = 02a) a = 0 e n < src="matematica/matematica-57ac25eceb6fd.gif" alt="seta" >
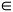an R3a) a > 0
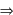an > 04a) a <>n par
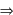an > 05a) a <>n ímpar
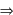an <>2. Propriedades
Consideremos os números reais a e b, e os números naturais m e n. Então são válidas as seguintes propriedades.
• P1: Produto de potências de mesma base
Para multiplicarmos potências de mesma base, conservamos a base e somamos os expoentes.
Justificativa:
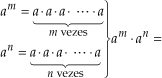
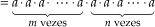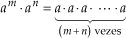
= Assim: am · an = am+n.
Exemplos:
a) 23 · 25 = 23+5 = 28
b) 4x · 4-x+2 = 4x+(-x+2) = 42
c) 3 · 32 · 36 = 31+2+6 = 39
• P2: Quociente de potências de mesma base
Para dividirmos potências de mesma base, conservamos a base e subtraímos os expoentes.
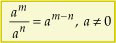
Justificativa:
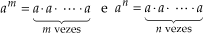
1o. Sendo m > n, temos
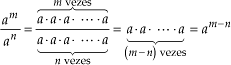
2o. Se m = n,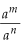 
= 1= a(m-n) = a0 = 1
3o. Se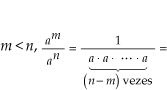
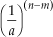= a (m - n)
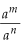= 1= a(m-n) = a0 = 13o. Se
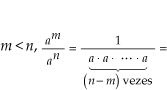
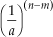= a (m - n) Exemplos:
a)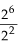 
= 26-2 = 24
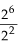= 26-2 = 24 b)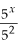 
= 5x-2
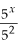= 5x-2 c)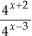 
= 4(x+2)-(x-3) = 45
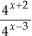= 4(x+2)-(x-3) = 45 • P3: Produto de potências de mesmo expoente
Para multiplicarmos potências de mesmo expoente, conservamos o expoente e multiplicamos as bases.
Justificativa
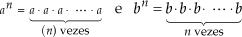
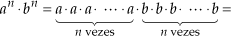
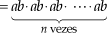
Assim: an · bn = (ab)n.
Exemplos
a) 24 · 84 = (2 · 8)4 = 164
b) x3 · y3 · z3 = (x · y · z)3
• P4: Quociente de potências de mesmo expoente
Para dividirmos potências de mesmo expoente, conservamos o expoente e dividimos as bases.
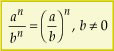
Justificativa:
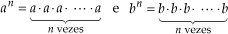
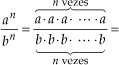
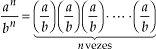
Assim:
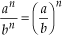
Exemplos:
a)
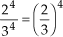
b)
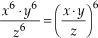
• P5: Potência de uma potência
Para elevarmos uma potência a um novo expoente, conservamos a base e multiplicamos os expoentes.
Justificativa:
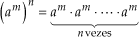
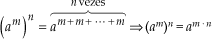
Exemplos:
a) (23)2 = 22.2 = 26
b)
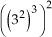= 32.3.2 = 312Observação
As propriedades apresentadas podem ser estendidas para os expoentes m e n inteiros.
Exemplos
a) 23 · 2-2 = 23 + (-2) = 21 (P1)
b)
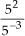= 52 - (-3) = 52 + 3 = 55 (P2)c) 5-3 · 2-3 = (5 · 2)-3 = 10-3 (P3)
d)
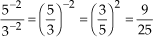(P4)e)
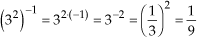(P5)Situações Especieais
A. (– a)n e –an
As potências (–a)n e –an , em geral, apresentam resultados diferentes, pois:
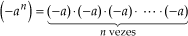
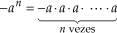
Exemplos
a) (–2)4 = (–2) · (–2) · (–2) · (–2) = 16
b) –24 = – 2 · 2 · 2 · 2 = –16
c) (–2)3 = (–2) · (–2) · (–2) = –8
d) –23 = – 2 · 2 · 2 = –8
B.
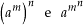
As potências
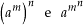, em geral, apresentam resultados diferentes, pois: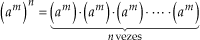e
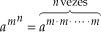
Exemplos
a)
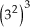= (32) · (32) · (32) = 32 · 3 = 36b)
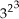= 32 · 2 · 2 = 38- Jura? Outra Forma De Calcular Potências Com Expoente 2
Olá pessoal, Normalmente, aprendemos no ensino fundamental como calcular potências. Vamos relembrar? Definição: Dado um certo número real qualquer (i), e um número n, inteiro e positivo, é definido in = potência de base (i) com expoente...
- Expressão Numérica C/ Potencia E Raiz
POTENCIAÇÃO E RADICIAÇÃO POTENCIAÇÃO Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes...
- Potenciação E Radiciação
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Potenciação
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br Representamos por an, a potência de base real a e expoente inteiro n....