Matemática
Progressão Aritmética é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior mais uma constante denominada de razão. Por exemplo, na sequência 2, 5, 8, 11, 14, 17, 20, 23, a razão é igual a 3, pois:
2 + 3 = 5
5 + 3 = 8
8 + 3 = 11
11 + 3 = 14
14 + 3 = 17
17 + 3 = 20
20 + 3 = 23
Em uma progressão aritmética temos que:
a1 (primeiro elemento)
r (razão)
an (representa o termo a ser procurado)
n (número de elementos da progressão)
No cálculo de qualquer um dos termos de uma PA, utilizamos a seguinte expressão matemática:
an = a1 + (n – 1) * r
Exemplo 1
Dada a progressão aritmética (3, 7, 11, 15, 19, 23,...), determine o 20º termo.
Razão
r = a2 – a1
r = 7 – 3
r = 4
Termo geral
an = a1 + (n – 1) * r
a20 = 3 + (20 – 1) * 4
a20 = 3 + 19 * 4
a20 = 3 + 76
a20 = 79
O vigésimo termo da PA é 79.
Exemplo 2
Determine o número de termos da seguinte progressão aritmética: (124, 131, 138, 145..., 572).
an = a1 + (n – 1) * r
572 = 124 + (n – 1) * 7
572 = 124 + 7n – 7
572 + 7 – 124 = 7n
455 = 7n
n = 455/7
n = 65
Exemplo 3
(EU – PA) A prefeitura de um município, preocupada com o êxodo rural, implantou um projeto de incentivo à agricultura orgânica, com previsão de três anos, para manter as pessoas no campo. Observou-se após a implantação que 12 famílias haviam sido beneficiadas no primeiro mês, 19 famílias, no segundo mês; e 26 famílias, no terceiro mês. Segundo os técnicos, a previsão é de que o número de famílias beneficiadas mensalmente aumente na mesma razão dos meses anteriores. Dentro dessas previsões, qual o número de famílias que serão beneficiadas no último mês de execução do projeto?
Duração do projeto será de 3 anos ou 36 meses (n)
Razão da PA será dada por 19 – 12 = 7
an = a1 + (n – 1) * r
a36 = 12 + (36 – 1) * 7
a36 = 12 + 35 * 7
a36 = 12 + 245
a36 = 257
O projeto municipal beneficiará 257 famílias.
Soma dos Termos de uma PA
Para determinarmos a soma dos termos de uma PA, utilizamos a seguinte expressão matemática:
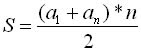
Exemplo 4
Dada a PA (14, 20, 26, ...194), determine a soma de seus termos.
Determinando o número de termos
an = a1 + (n – 1) * r
194 = 14 + (n – 1) * 6
194 = 14 + 6n – 6
194 + 6 – 14 = 6n
200 – 14 = 6n
6n = 186
n = 186/6
n = 31
Soma dos termos
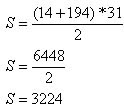
www.bancodeconcursos.com
- Progressão Aritmetica
As atividades envolvendo progressões exigem atenção por parte dos estudantes, pois devemos ter conhecimento das fórmulas matemáticas na resolução das progressões. A partir da interpretação do enunciado deveremos escolher qual a fórmula adequada....
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- Progressão Aritmetica
Sucessões ou Seqüências DEFINIÇÃO Conjuntos de objetos de qualquer natureza, organizados ou escritos numa ordem bem determinada. Para representar uma seqüência, escrevemos seus elementos, ou termos, entre parênteses. É importante destacar que,...
- Progressão Aritmética
Sucessões ou Seqüências DEFINIÇÃO Conjuntos de objetos de qualquer natureza, organizados ou escritos numa ordem bem determinada. Para representar uma seqüência, escrevemos seus elementos, ou termos, entre parênteses. É importante destacar que,...
- Progressão Geométrica
Progressão Geométrica é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior multiplicado por uma constante denominada de razão. Por exemplo, na sequência 2, 6, 18, 54, 162, 486, 1 458, 4 374, 13 122, a razão...
Matemática
Progressão Aritmética
Progressão Aritmética é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior mais uma constante denominada de razão. Por exemplo, na sequência 2, 5, 8, 11, 14, 17, 20, 23, a razão é igual a 3, pois:
2 + 3 = 5
5 + 3 = 8
8 + 3 = 11
11 + 3 = 14
14 + 3 = 17
17 + 3 = 20
20 + 3 = 23
Em uma progressão aritmética temos que:
a1 (primeiro elemento)
r (razão)
an (representa o termo a ser procurado)
n (número de elementos da progressão)
No cálculo de qualquer um dos termos de uma PA, utilizamos a seguinte expressão matemática:
an = a1 + (n – 1) * r
Exemplo 1
Dada a progressão aritmética (3, 7, 11, 15, 19, 23,...), determine o 20º termo.
Razão
r = a2 – a1
r = 7 – 3
r = 4
Termo geral
an = a1 + (n – 1) * r
a20 = 3 + (20 – 1) * 4
a20 = 3 + 19 * 4
a20 = 3 + 76
a20 = 79
O vigésimo termo da PA é 79.
Exemplo 2
Determine o número de termos da seguinte progressão aritmética: (124, 131, 138, 145..., 572).
an = a1 + (n – 1) * r
572 = 124 + (n – 1) * 7
572 = 124 + 7n – 7
572 + 7 – 124 = 7n
455 = 7n
n = 455/7
n = 65
Exemplo 3
(EU – PA) A prefeitura de um município, preocupada com o êxodo rural, implantou um projeto de incentivo à agricultura orgânica, com previsão de três anos, para manter as pessoas no campo. Observou-se após a implantação que 12 famílias haviam sido beneficiadas no primeiro mês, 19 famílias, no segundo mês; e 26 famílias, no terceiro mês. Segundo os técnicos, a previsão é de que o número de famílias beneficiadas mensalmente aumente na mesma razão dos meses anteriores. Dentro dessas previsões, qual o número de famílias que serão beneficiadas no último mês de execução do projeto?
Duração do projeto será de 3 anos ou 36 meses (n)
Razão da PA será dada por 19 – 12 = 7
an = a1 + (n – 1) * r
a36 = 12 + (36 – 1) * 7
a36 = 12 + 35 * 7
a36 = 12 + 245
a36 = 257
O projeto municipal beneficiará 257 famílias.
Soma dos Termos de uma PA
Para determinarmos a soma dos termos de uma PA, utilizamos a seguinte expressão matemática:
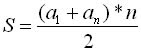
Exemplo 4
Dada a PA (14, 20, 26, ...194), determine a soma de seus termos.
Determinando o número de termos
an = a1 + (n – 1) * r
194 = 14 + (n – 1) * 6
194 = 14 + 6n – 6
194 + 6 – 14 = 6n
200 – 14 = 6n
6n = 186
n = 186/6
n = 31
Soma dos termos
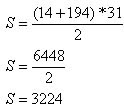
www.bancodeconcursos.com
- Progressão Aritmetica
As atividades envolvendo progressões exigem atenção por parte dos estudantes, pois devemos ter conhecimento das fórmulas matemáticas na resolução das progressões. A partir da interpretação do enunciado deveremos escolher qual a fórmula adequada....
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- Progressão Aritmetica
Sucessões ou Seqüências DEFINIÇÃO Conjuntos de objetos de qualquer natureza, organizados ou escritos numa ordem bem determinada. Para representar uma seqüência, escrevemos seus elementos, ou termos, entre parênteses. É importante destacar que,...
- Progressão Aritmética
Sucessões ou Seqüências DEFINIÇÃO Conjuntos de objetos de qualquer natureza, organizados ou escritos numa ordem bem determinada. Para representar uma seqüência, escrevemos seus elementos, ou termos, entre parênteses. É importante destacar que,...
- Progressão Geométrica
Progressão Geométrica é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior multiplicado por uma constante denominada de razão. Por exemplo, na sequência 2, 6, 18, 54, 162, 486, 1 458, 4 374, 13 122, a razão...
