Matemática
De acordo com essas informações, o coeficiente do termo contendo os fatores x5y2 no desenvolvimento de (2x + y)7 é
***
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Triangulo De Pascal
Triangulo de Pascal A Relação de Stifel é usada principalmente na construção do Triângulo de Pascal. Definição O Triângulo de Pascal também é conhecido como Triângulo de Tartaglia, trata-se de uma tabela triangular formada por números binomiais...
- O Triângulo De Pascal
O triângulo de Pascal tem o objetivo de dispor os coeficientes binomiais, de modo que os coeficientes de mesmo numerador agrupem-se em uma mesma linha, e coeficientes de mesmo denominador agrupem-se na mesma coluna. O coeficiente binomial de dois números...
- O Triângulo De Pascal
O triângulo de Pascal tem o objetivo de dispor os coeficientes binomiais, de modo que os coeficientes de mesmo numerador agrupem-se em uma mesma linha, e coeficientes de mesmo denominador agrupem-se na mesma coluna. O coeficiente binomial de dois números...
- Triângulo De Pascal
Triangulo de Pascal A Relação de Stifel é usada principalmente na construção do Triângulo de Pascal. Definição O Triângulo de Pascal também é conhecido como Triângulo de Tartaglia, trata-se de uma tabela triangular formada por números binomiais...
Matemática
Questão 51 ? F.C.C. ? 2.011 ? S.E.E. ? MA ? Professor de Matemática ? E.M.R.
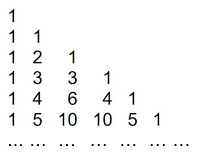
O seguinte arranjo de números é conhecido como triângulo de Pascal:
Sabe-se que os números do triângulo de Pascal correspondem aos coeficientes do desenvolvimento de (a + b)n, segundo as potências decrescentes de a.
De acordo com essas informações, o coeficiente do termo contendo os fatores x5y2 no desenvolvimento de (2x + y)7 é (A) 672
(B) 480
(C) 240
(D) 32
(E) 21
Solução: (A)
Na resolução utilizaremos também os conceitos do Binômio de Newton.
Para continuar o triângulo de Pascal temos que observar que cada elemento do triângulo que não seja da primeira coluna da esquerda e nem o último de cada linha é igual à soma daquele elemento que está logo acima na mesma coluna com o elemento que se situa à esquerda deste último.
Na primeira coluna a esquerda todos os elementos são iguais a 1, o mesmo ocorre com o ultimo elemento em casa linha que também deve ser igual a 1.
Observe a Figura 1:
Para construir o triângulo de Pascal é melhor montá-lo na forma de um triângulo isósceles. Comece com ?1? no topo, em seguida, coloque ?1? e ?1?, na segunda linha. Agora devemos observar que a cada linha começa e termina com 1 e os elementos no meio da linha são formados pelas somas dos números que estão logo acima.
 |
| Figura 1: Construção do Triângulo de Pascal (relação de Stifel). |
Para construir o triângulo de Pascal é melhor montá-lo na forma de um triângulo isósceles. Comece com ?1? no topo, em seguida, coloque ?1? e ?1?, na segunda linha. Agora devemos observar que a cada linha começa e termina com 1 e os elementos no meio da linha são formados pelas somas dos números que estão logo acima.
Observe a Figura 2 para entender melhor a construção:
Segundo o enunciado cada linha do triângulo de pascal corresponde aos coeficientes do desenvolvimento de (a + b)n, segundo as potências decrescentes de a, conforme pode ser observado na Figura 3.
 |
| Figura 2: Construção do Triângulo de Pascal. |
Segundo o enunciado cada linha do triângulo de pascal corresponde aos coeficientes do desenvolvimento de (a + b)n, segundo as potências decrescentes de a, conforme pode ser observado na Figura 3.
 |
| Figura 3: Relação entre cada linha do Triângulo de Pascal e os coeficientes do desenvolvimento de (a + b)n . |
Por exemplo, na terceira linha temos os coeficientes do desenvolvimento de (a + b)2, ou seja, {1, 2, 1}, conforme podemos observar:
(a + b)2= a2 + 2·a·b + b2 = 1·a2+ 2·a·b + 1·b2
Na Figura 3, notamos que para (a + b)7, os coeficientes são {1, 7, 21, 35, 35, 21, 7, 1}.
O triângulo de Pascal gerou os coeficientes dos termos, agora o Binômio de Newton gera a parte literal dos termos.
Na prática, para utilizar o Binômio de Newton, colocamos os temos a serem desenvolvidos da seguinte forma: o primeiro termo elevado a potência maior (no nosso caso 7) e o segundo termo elevado a zero; a cada nova parcela do desenvolvimento o expoente do primeiro termo decresce em uma unidade, enquanto o primeiro termo cresce em uma unidade.
Na prática, para utilizar o Binômio de Newton, colocamos os temos a serem desenvolvidos da seguinte forma: o primeiro termo elevado a potência maior (no nosso caso 7) e o segundo termo elevado a zero; a cada nova parcela do desenvolvimento o expoente do primeiro termo decresce em uma unidade, enquanto o primeiro termo cresce em uma unidade.
Observe:
(a + b)7= a7·b0 + 7·a6·b1 + 21·a5·b2+ 35·a4·b3 + 35·a3·b4 + 21·a2·b5+ 7·a1·b6 + a0·b7
(a + b)7= a7 + 7·a6·b + 21·a5·b2 + 35·a4·b3+ 35·a3·b4 + 21·a2·b5 + 7·a·b6+ b7
O enunciado pede para calcular o coeficiente que acompanha os fatores x5 · y2 no desenvolvimento de (2 · x + y)7, segundo calculado acima, isto ocorre na terceira parcela:
Se a = 2 · x e b = y, então:
Se a = 2 · x e b = y, então:
21 · a5 · b2= 21 · (2 · x)5 · y2 = 21 · 25 · x5 · y2 = 21 · 32 · x5· y2 = 672 · x5 · y2
Então o coeficiente que acompanha os fatores x5 · y2 é 672.
 Professor compartilhe sua criatividade! |  Compartilhe esta ideia de divulgar a Matemática! |
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Triangulo De Pascal
Triangulo de Pascal A Relação de Stifel é usada principalmente na construção do Triângulo de Pascal. Definição O Triângulo de Pascal também é conhecido como Triângulo de Tartaglia, trata-se de uma tabela triangular formada por números binomiais...
- O Triângulo De Pascal
O triângulo de Pascal tem o objetivo de dispor os coeficientes binomiais, de modo que os coeficientes de mesmo numerador agrupem-se em uma mesma linha, e coeficientes de mesmo denominador agrupem-se na mesma coluna. O coeficiente binomial de dois números...
- O Triângulo De Pascal
O triângulo de Pascal tem o objetivo de dispor os coeficientes binomiais, de modo que os coeficientes de mesmo numerador agrupem-se em uma mesma linha, e coeficientes de mesmo denominador agrupem-se na mesma coluna. O coeficiente binomial de dois números...
- Triângulo De Pascal
Triangulo de Pascal A Relação de Stifel é usada principalmente na construção do Triângulo de Pascal. Definição O Triângulo de Pascal também é conhecido como Triângulo de Tartaglia, trata-se de uma tabela triangular formada por números binomiais...