Matemática
Nesta postagem, vamos provar que:
\begin{equation*}
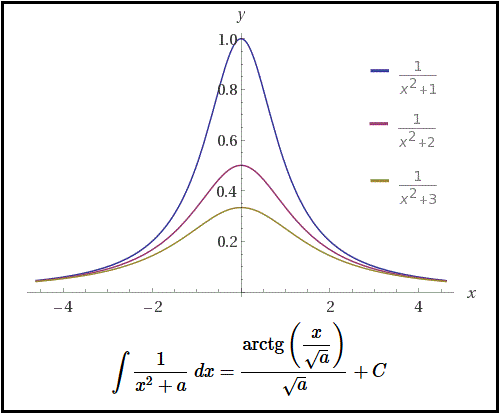
\int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C
\end{equation*}
onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq 0$.
Seja a integral:
\begin{equation*}
I = \int \frac{1}{x^2+a}\ dx
\end{equation*}
Fatorando o denominador do integrando:
\begin{equation*}
I = \int \frac{1}{\displaystyle a\left(\frac{x^2}{a}+1\right)}\ dx
\end{equation*}
Fatorando as constantes:
\begin{equation*}
I = \frac{1}{a}\int \frac{1}{\displaystyle \frac{x^2}{a}+1}\ dx
\end{equation*}
Para o integrando, fazemos a substituição $\displaystyle u=\frac{x}{\sqrt{a}}$. Assim, $\displaystyle du = \frac{1}{\sqrt{a}}$ e $dx = \sqrt{a}\ du$:
\begin{equation*}
I = \frac{1}{a} \int \frac{1}{u^2 + 1}\ \sqrt{a}\ du \\
\ \\
I = \frac{\sqrt{a}}{a} \int \frac{1}{u^2 +1}\ du \\
\ \\
I = \frac{1}{\sqrt{a}} \int \frac{1}{u^2+1}\ du
\end{equation*}
A integral de $\displaystyle \frac{1}{u^2+1}$ é $\text{arctg}(u)$. Assim:
\begin{equation*}
I = \frac{\text{arctg}(u)}{\sqrt{a}} + C
\end{equation*}
Mas, $\displaystyle u = \frac{x}{\sqrt{a}}$. Logo:
\begin{equation*}
I = \frac{\displaystyle \text{arctg}\left(\frac{x}{\sqrt{a}}\right)}{\sqrt{a}} + C
\end{equation*}
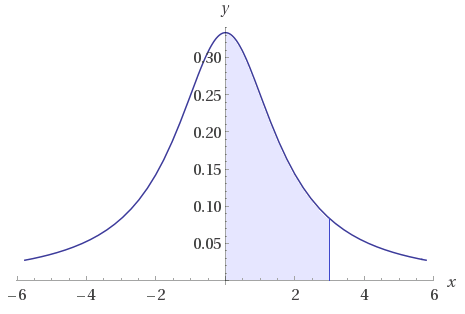
A área sob a curva é dada pela integral definida com limites de integração iguais a $0$ e $3$:
\begin{equation*}
A = \int_0^3 \frac{1}{x^2+3}\ dx = \left[ \frac{\displaystyle \text{arctg}\left(\frac{x}{\sqrt{3}}\right)}{\sqrt{3}} \right]_0^3\\
\ \\
A = \frac{\displaystyle \text{arctg}\left(\frac{3}{\sqrt{3}}\right)}{\sqrt{3}} - \frac{\displaystyle \text{arctg}\left(\frac{0}{\sqrt{3}}\right)}{\sqrt{3}}\\
\ \\
A = \frac{\text{arctg}(\sqrt{3})}{\sqrt{3}} - \frac{\text{arctg}(0)}{\sqrt{3}}
\end{equation*}
O arco cuja tangente vale $\sqrt{3}$ é o ângulo de $60^\circ$ e mede $\displaystyle \frac{\pi}{3}$ radianos. Já o arco cuja tangente vale $0^\circ$ é o arco nulo. Assim:
\begin{equation*}
A = \frac{\pi}{3\sqrt{3}} - 0 \approx 0,6046
\end{equation*}
Resposta: A área sob a curva $\displaystyle f(x) = \frac{1}{x^2+a}$, compreendida no intervalo $[0,3]$ mede aproximadamente $0,6046$ unidades de área.
Integração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}(ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}(ax)dx = - \frac{\cos(ax)}{a}+C \end{equation*} onde $a \in \mathbb{R}$ e $a\neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}(ax)dx \end{equation*} Para o integrando...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Resolução da integral $\displaystyle \int \frac{1}{x^2+a}\ dx$
Nesta postagem, vamos provar que:
\begin{equation*}
\int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C
\end{equation*}
onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq 0$.

Seja a integral:
\begin{equation*}
I = \int \frac{1}{x^2+a}\ dx
\end{equation*}
Fatorando o denominador do integrando:
\begin{equation*}
I = \int \frac{1}{\displaystyle a\left(\frac{x^2}{a}+1\right)}\ dx
\end{equation*}
Fatorando as constantes:
\begin{equation*}
I = \frac{1}{a}\int \frac{1}{\displaystyle \frac{x^2}{a}+1}\ dx
\end{equation*}
Para o integrando, fazemos a substituição $\displaystyle u=\frac{x}{\sqrt{a}}$. Assim, $\displaystyle du = \frac{1}{\sqrt{a}}$ e $dx = \sqrt{a}\ du$:
\begin{equation*}
I = \frac{1}{a} \int \frac{1}{u^2 + 1}\ \sqrt{a}\ du \\
\ \\
I = \frac{\sqrt{a}}{a} \int \frac{1}{u^2 +1}\ du \\
\ \\
I = \frac{1}{\sqrt{a}} \int \frac{1}{u^2+1}\ du
\end{equation*}
A integral de $\displaystyle \frac{1}{u^2+1}$ é $\text{arctg}(u)$. Assim:
\begin{equation*}
I = \frac{\text{arctg}(u)}{\sqrt{a}} + C
\end{equation*}
Mas, $\displaystyle u = \frac{x}{\sqrt{a}}$. Logo:
\begin{equation*}
I = \frac{\displaystyle \text{arctg}\left(\frac{x}{\sqrt{a}}\right)}{\sqrt{a}} + C
\end{equation*}
Exemplo:
Calcular a área sob a curva $\displaystyle f(x) = \frac{1}{x^2+3}$ compreendida no intervalo $[0,3]$.
A área sob a curva é dada pela integral definida com limites de integração iguais a $0$ e $3$:
\begin{equation*}
A = \int_0^3 \frac{1}{x^2+3}\ dx = \left[ \frac{\displaystyle \text{arctg}\left(\frac{x}{\sqrt{3}}\right)}{\sqrt{3}} \right]_0^3\\
\ \\
A = \frac{\displaystyle \text{arctg}\left(\frac{3}{\sqrt{3}}\right)}{\sqrt{3}} - \frac{\displaystyle \text{arctg}\left(\frac{0}{\sqrt{3}}\right)}{\sqrt{3}}\\
\ \\
A = \frac{\text{arctg}(\sqrt{3})}{\sqrt{3}} - \frac{\text{arctg}(0)}{\sqrt{3}}
\end{equation*}
O arco cuja tangente vale $\sqrt{3}$ é o ângulo de $60^\circ$ e mede $\displaystyle \frac{\pi}{3}$ radianos. Já o arco cuja tangente vale $0^\circ$ é o arco nulo. Assim:
\begin{equation*}
A = \frac{\pi}{3\sqrt{3}} - 0 \approx 0,6046
\end{equation*}
Resposta: A área sob a curva $\displaystyle f(x) = \frac{1}{x^2+a}$, compreendida no intervalo $[0,3]$ mede aproximadamente $0,6046$ unidades de área.
Veja mais:
Lista de resolução de integraisIntegração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}(ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}(ax)dx = - \frac{\cos(ax)}{a}+C \end{equation*} onde $a \in \mathbb{R}$ e $a\neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}(ax)dx \end{equation*} Para o integrando...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
