Matemática
A forma canónica da equação cúbica ou do 3.º grau é:
 com
com 
O método de resolução usual começa por transformá-la noutra, fazendo a substituição :
:
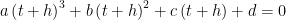


? uma nova equação cúbica (em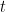 ) à qual falta o termo do 2.º grau:
) à qual falta o termo do 2.º grau:

cujos coeficientes são:
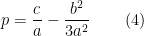
e
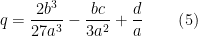
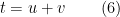

Uma solução de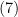 é a dada pelo sistema em
é a dada pelo sistema em  e
e 

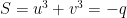 e o produto
e o produto 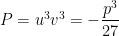 .
.
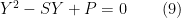

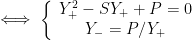
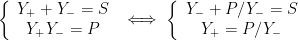


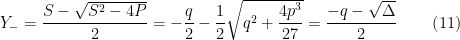
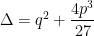 .
.


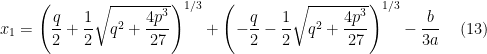
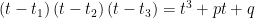
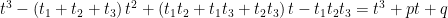


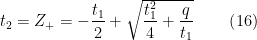




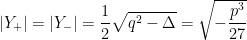
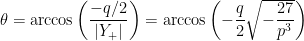
![\left\{\begin{array}{c}\sqrt[3]{Y_{+}}=\sqrt{-\dfrac{p}{3}}\left(\cos \left( \dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) +i\sin\left(\dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) \right)\\\\\sqrt[3]{Y_{-}}=\sqrt{-\dfrac{p}{3}}\left( \cos \left( \dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) -i\sin \left(\dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) \right) \end{array}\right.\qquad \left( 19\right) \left\{\begin{array}{c}\sqrt[3]{Y_{+}}=\sqrt{-\dfrac{p}{3}}\left(\cos \left( \dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) +i\sin\left(\dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) \right)\\\\\sqrt[3]{Y_{-}}=\sqrt{-\dfrac{p}{3}}\left( \cos \left( \dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) -i\sin \left(\dfrac{\theta }{3}+\dfrac{2k\pi }{3}\right) \right) \end{array}\right.\qquad \left( 19\right)](http://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bc%7D%5Csqrt%5B3%5D%7BY_%7B%2B%7D%7D%3D%5Csqrt%7B-%5Cdfrac%7Bp%7D%7B3%7D%7D%5Cleft%28%5Ccos+%5Cleft%28+%5Cdfrac%7B%5Ctheta+%7D%7B3%7D%2B%5Cdfrac%7B2k%5Cpi+%7D%7B3%7D%5Cright%29+%2Bi%5Csin%5Cleft%28%5Cdfrac%7B%5Ctheta+%7D%7B3%7D%2B%5Cdfrac%7B2k%5Cpi+%7D%7B3%7D%5Cright%29+%5Cright%29%5C%5C%5C%5C%5Csqrt%5B3%5D%7BY_%7B-%7D%7D%3D%5Csqrt%7B-%5Cdfrac%7Bp%7D%7B3%7D%7D%5Cleft%28+%5Ccos+%5Cleft%28+%5Cdfrac%7B%5Ctheta+%7D%7B3%7D%2B%5Cdfrac%7B2k%5Cpi+%7D%7B3%7D%5Cright%29+-i%5Csin+%5Cleft%28%5Cdfrac%7B%5Ctheta+%7D%7B3%7D%2B%5Cdfrac%7B2k%5Cpi+%7D%7B3%7D%5Cright%29+%5Cright%29+%5Cend%7Barray%7D%5Cright.%5Cqquad+%5Cleft%28+19%5Cright%29+&bg=ffffff&fg=000000&s=0)


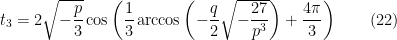

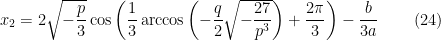

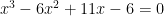




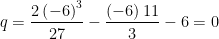

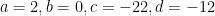

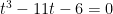
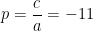
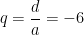

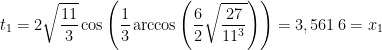

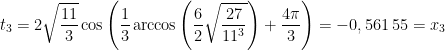



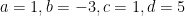

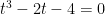
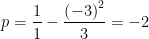
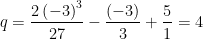
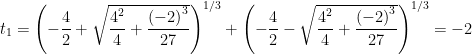


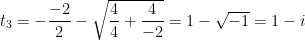


- Equação Do 2º Grau
matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas. Veja: 2x + 1 = 0, o expoente da incógnita x é igual a 1....
- Equação Do 2º Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais e...
- Equação Do Segundo Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais...
- Equação Completa Do Segundo Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais...
- Equações Biquadradas
A resolução de equações e a criação de fórmulas que encontram suas soluções sempre foram objetos de estudo da matemática. Geralmente, as equações estão associadas a situações reais em que se deseja descobrir a melhor alternativa para a...
Matemática
Resolução de Equações do 3º Grau ou Cúbicas
A forma canónica da equação cúbica ou do 3.º grau é:
O método de resolução usual começa por transformá-la noutra, fazendo a substituição
Dividindo por  e ordenando o polinómio do lado esquerdo pelas potências decrescente de
e ordenando o polinómio do lado esquerdo pelas potências decrescente de 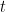 , obtemos ? se escolhermos
, obtemos ? se escolhermos 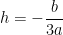
? uma nova equação cúbica (em
cujos coeficientes são:
e
Se exprimirmos a variável 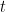 na soma de duas outras
na soma de duas outras
a equação  transforma-se em
transforma-se em
Uma solução de
Somos assim conduzidos ao problema de achar dois números 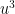 e
e  dos quais se sabe a soma
dos quais se sabe a soma
Como é bem sabido esses números são as duas soluções  e
e 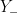 da equação auxiliar do 2.º grau:
da equação auxiliar do 2.º grau:
De fato
e
Resolvendo-a determinamos
Nesta notação o discriminante 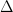 é igual a
é igual a
Consideremos, sem perda de generalidade, 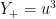 e
e  . Introduzindo
. Introduzindo  e
e 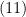 em
em 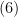 , obtemos
, obtemos
a solução ![t_{1}=\sqrt[3]{Y_{+}}+\sqrt[3]{Y_{-}} t_{1}=\sqrt[3]{Y_{+}}+\sqrt[3]{Y_{-}}](http://s0.wp.com/latex.php?latex=t_%7B1%7D%3D%5Csqrt%5B3%5D%7BY_%7B%2B%7D%7D%2B%5Csqrt%5B3%5D%7BY_%7B-%7D%7D&bg=ffffff&fg=000000&s=0) :
:
ou seja
e uma solução da equação inicial
Conhecida a solução  , podemos determinar as duas restantes
, podemos determinar as duas restantes 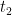 e
e 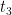 decompondo o polinómio do primeiro
decompondo o polinómio do primeiro
membro de  num produto de fatores lineares:
num produto de fatores lineares:
ou
Os dois polinómios são equivantes se tiverem iguais coeficientes homólogos:
Novamente temos de determinar dois números 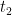 e
e 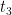 dos quais se conhece a soma (
dos quais se conhece a soma ( ) e o produto
) e o produto
( ). Para esse fim formamos a equação do 2.º grau:
). Para esse fim formamos a equação do 2.º grau:
que resolvida dá as soluções
As três soluções da equação em  são então:
são então:
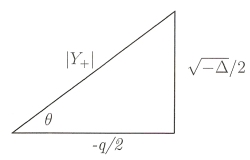
No caso do discriminante ser negativo, 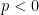 , convertemos os complexos conjugados
, convertemos os complexos conjugados  e
e 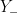 à forma trigonométrica
à forma trigonométrica

Os módulos são iguais:
e os argumentos são simétricos, sendo o de  :
:
As três raízes cúbicas de  e
e 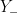 são (
são ( )
)
Obtemos, respectivamente, para 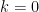 ,
, 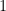 e
e 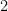 as três soluções da equação
as três soluções da equação  :
:
e as da equação original  :
:
EXEMPLOS
1. DETERMINE AS SOLUÇÕES DA EQUAÇÃO:
Os coeficientes são:
Pondo
a equação transforma-se em:
uma vez que os seus coeficientes são:
e
As suas soluções são 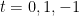 , a que correspondem as da equação na forma canónica
, a que correspondem as da equação na forma canónica 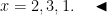
2. RESOLVA A EQUAÇÃO
Agora temos
Como era de esperar a substituição é
e os coeficientes da equação em 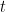
são simplesmente os da equação inicial divididos por 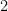 :
:
e
O discriminante é negativo
Assim, como 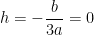 :
:
Tentando diminuir os erros de cálculo, reparemos que o inteiro 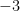 é uma solução. Se recalcularmos as outras duas, obtemos as soluções exatas:
é uma solução. Se recalcularmos as outras duas, obtemos as soluções exatas:
e
3. RESOLVA A EQUAÇÃO
Os coeficientes são:
Fazendo a substituição
obtém-se a equação
em que
e
Uma solução da equação em 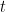 é dada pela fórmula:
é dada pela fórmula:
a que corresponde a solução da equação em  :
:
As restantes soluções da equação em 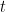 são
são
e, portanto, as da equação em  são
são
REFERÊNCIAS
Blog Problemas e Teoremas.
- Equação Do 2º Grau
matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas. Veja: 2x + 1 = 0, o expoente da incógnita x é igual a 1....
- Equação Do 2º Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais e...
- Equação Do Segundo Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais...
- Equação Completa Do Segundo Grau
As equações do tipo ax + b = 0, com a e b números reais e a ≠ 0 são consideradas equações do 1º grau, e podem ter no máximo um resultado. Os modelos de expressões que satisfazem a condição ax² + bx + c = 0, com a, b e c números reais...
- Equações Biquadradas
A resolução de equações e a criação de fórmulas que encontram suas soluções sempre foram objetos de estudo da matemática. Geralmente, as equações estão associadas a situações reais em que se deseja descobrir a melhor alternativa para a...
