Matemática
O sistema binário de computação já era conhecido na China uns 3000 a.C., de acordo com os manuscritos da época. Quarenta e seis séculos depois, Leibniz redescobre o sistema binário.
Este sistema de numeração binário é muito importante, na medida em que, modernamente, é de largo alcance por ser utilizado nas calculadoras electrónicas, computadores e nas estruturas que envolvem relações binárias. Este sistema pode ser chamado sistema de base dois, binário ou dual, o qual utiliza apenas dois algarismos, o 0 e o 1, os quais nas estruturas dessas máquinas se fazem corresponder às situações de sim-não, aberto-fechado, contacto-interrupção, passagem-vedação, etc., uma vez que os circuitos digitais são constituídos por elementos dotados de dois estados distintos.
A cada um dos símbolos do sistema binário chama-se um «bit».
O maior inconveniente da base dois é que a representação de cada número envolve muitos algarismos. Por exemplo, cem mil, que na base dez se representa por 5 algarismos, na base dois representa-se por 17 algarismos! Porém, este inconveniente é superado nas máquinas electrónicas pela velocidade.
Como é que funciona, afinal, este sistema binário?
Na base dois, um número imediatamente à esquerda de outro, representa, em relação a este, um número de unidades duas vezes maior. (..., 2 3, 2 2, 21, 20)
Como é que se representa um número decimal (numeração árabe) na base dois?
Temos então que, para passar da notação binária para a notação decimal, o processo não é muito complexo e é o seguinte, por exemplo:
10011010(2)=1×27+0×26+0×25+1×24+1×23+0×22+1×21+0×20
= 128+0+0+16+8+0+2+0=
=154(10) (O que é uma maneira bem mais prática de representar o mesmo número!)
8(10)= ?(2)
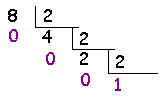Podemos então concluir que 8(10)=1000(2) ( 8 = 1×2³+ +0×2²+ 0×2¹+0×20)
Vejamos este outro exemplo:
66(10)= ?(2)
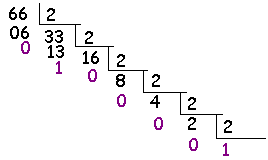Podemos então concluir que 66(10)=1000010(2) ( 66 = 1×26+ + 0×25+0×24+0×23+0×22+1×21+0×20 )
- Questão 13 ? Certificação De Competências Etec ? Técnico Em Eletrônica ? 2° Semestre De 2.014
Em circuitos digitais, é comum o uso de números binários. Qual das alternativas a seguir apresenta um número binário de quatro dígitos? (A) 4321(B) 5588(C) 0101(D) 0220(E) 0102 Solução: (C) No sistema de numeração binário são utilizados apenas...
- Questão 22 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
Um professor do 6.º ano, para destacar uma das principais características do Sistema de Numeração Decimal, que é o valor posicional dos símbolos, propôs diversas atividades a seus alunos envolvendo outras bases além da base dez. Em uma dessas...
- Sistema De Numeração Binario
O sistema decimal é muito usado no cotidiano, pois nos oferece uma forma mais simples de manipular os números em determinadas situações matemáticas, é composto por dez números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. O uso da Matemática em situações diversas...
- Sistema De Numeração Decimal
O sistema de numeração que usamos é um sistema decimal, pois contamos em grupos de 10. A palavra decimal tem origem na palavra latina decem, que significa 10. Ele foi inventado pelos hindus, aperfeiçoado e levado para a Europa pelos árabes. Daí...
- Potências Em Base Decimal, Base Binária E O Byte
As unidades de memória dos computadores são amplamente conhecidas hoje em dia. O uso de termos como megabytes ou gigabytes para se referir à capacidade de memória de dispositivos como HD, memórias ou Pendrives está muito comum no cotidiano do mundo...
Matemática
sistema binário
O sistema binário de computação já era conhecido na China uns 3000 a.C., de acordo com os manuscritos da época. Quarenta e seis séculos depois, Leibniz redescobre o sistema binário.
Este sistema de numeração binário é muito importante, na medida em que, modernamente, é de largo alcance por ser utilizado nas calculadoras electrónicas, computadores e nas estruturas que envolvem relações binárias. Este sistema pode ser chamado sistema de base dois, binário ou dual, o qual utiliza apenas dois algarismos, o 0 e o 1, os quais nas estruturas dessas máquinas se fazem corresponder às situações de sim-não, aberto-fechado, contacto-interrupção, passagem-vedação, etc., uma vez que os circuitos digitais são constituídos por elementos dotados de dois estados distintos.
O maior inconveniente da base dois é que a representação de cada número envolve muitos algarismos. Por exemplo, cem mil, que na base dez se representa por 5 algarismos, na base dois representa-se por 17 algarismos! Porém, este inconveniente é superado nas máquinas electrónicas pela velocidade.
Na base dois, um número imediatamente à esquerda de outro, representa, em relação a este, um número de unidades duas vezes maior. (..., 2 3, 2 2, 21, 20)
Como é que se representa um número decimal (numeração árabe) na base dois?
Vejamos os seguintes exemplos:
| Notação decimal | Notação binária |
|---|---|
| 0 | 0 ( =0×20 ) |
| 1 | 1 ( =1×20 ) |
| 2 | 10 ( =1×21+0×20) |
| 3 | 11 ( =1×21+1×20) |
| 4 | 100 ( =1×22+0×21+0×20) |
| 5 | 101 ( =1×22+0×21+1×20) |
| 6 | 110 ( =1×22+1×21+0×20) |
| 7 | 111 ( =1×22+1×21+1×20) |
10011010(2)=1×27+0×26+0×25+1×24+1×23+0×22+1×21+0×20
= 128+0+0+16+8+0+2+0=
=154(10) (O que é uma maneira bem mais prática de representar o mesmo número!)
Como é que se passa da base decimal para a base binária?
Agora o processo é um pouco mais complexo, mas não deixa de ser interessante, vejamos os seguintes exemplos:8(10)= ?(2)
Façamos o seguinte raciocínio:
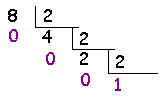
Vejamos este outro exemplo:
66(10)= ?(2)
Fonte: www.educ.fc.ul.pt
- Questão 13 ? Certificação De Competências Etec ? Técnico Em Eletrônica ? 2° Semestre De 2.014
Em circuitos digitais, é comum o uso de números binários. Qual das alternativas a seguir apresenta um número binário de quatro dígitos? (A) 4321(B) 5588(C) 0101(D) 0220(E) 0102 Solução: (C) No sistema de numeração binário são utilizados apenas...
- Questão 22 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
Um professor do 6.º ano, para destacar uma das principais características do Sistema de Numeração Decimal, que é o valor posicional dos símbolos, propôs diversas atividades a seus alunos envolvendo outras bases além da base dez. Em uma dessas...
- Sistema De Numeração Binario
O sistema decimal é muito usado no cotidiano, pois nos oferece uma forma mais simples de manipular os números em determinadas situações matemáticas, é composto por dez números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. O uso da Matemática em situações diversas...
- Sistema De Numeração Decimal
O sistema de numeração que usamos é um sistema decimal, pois contamos em grupos de 10. A palavra decimal tem origem na palavra latina decem, que significa 10. Ele foi inventado pelos hindus, aperfeiçoado e levado para a Europa pelos árabes. Daí...
- Potências Em Base Decimal, Base Binária E O Byte
As unidades de memória dos computadores são amplamente conhecidas hoje em dia. O uso de termos como megabytes ou gigabytes para se referir à capacidade de memória de dispositivos como HD, memórias ou Pendrives está muito comum no cotidiano do mundo...