Matemática

Supremo Quadrado Mágico Pitagórico

O triângulo da Figura 1 é um triângulo retângulo, desta forma podemos aplicar o Teorema de Pitágoras.

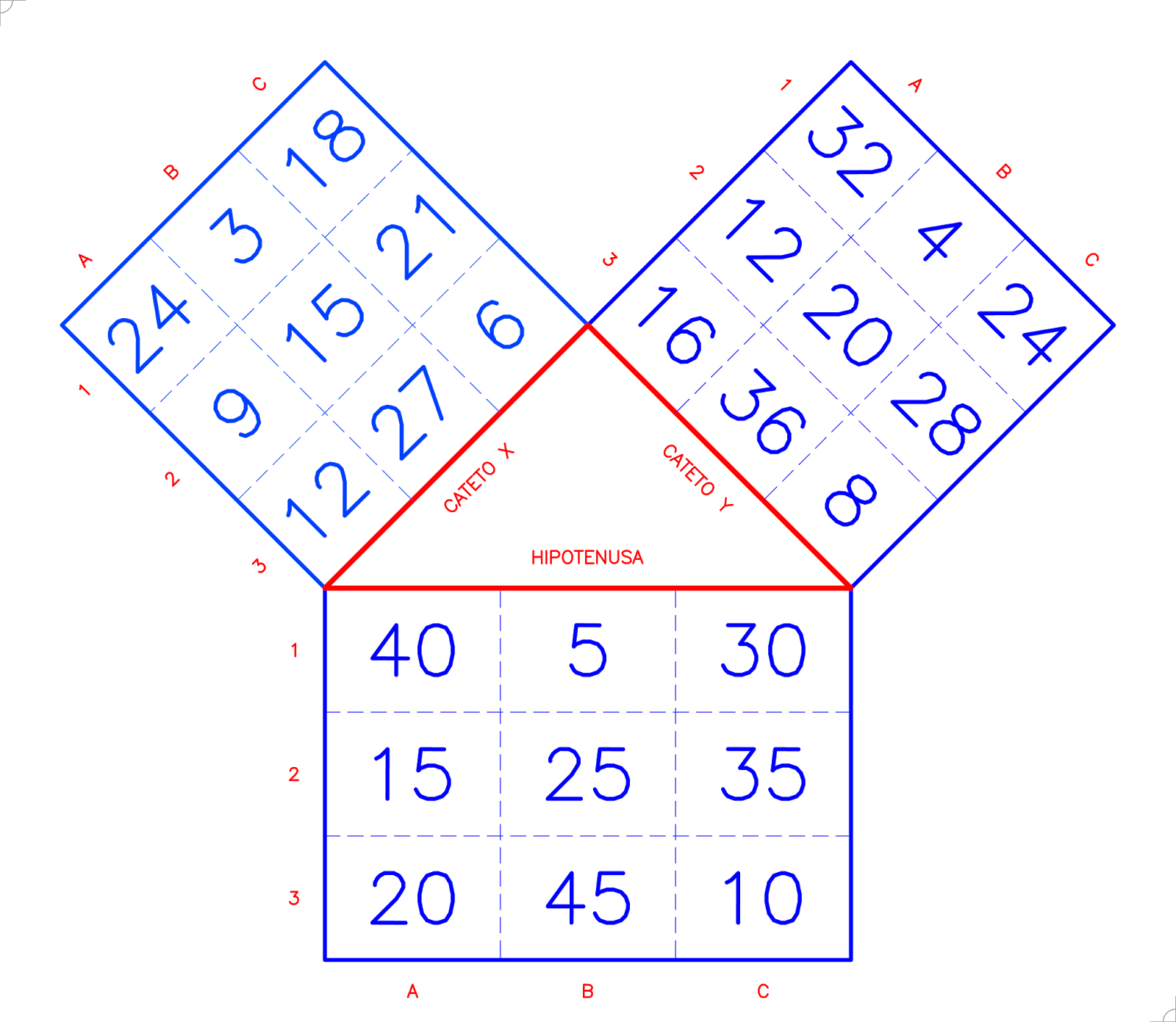Figura 1: Quadrado Mágico Pitagórico

Se você examinar a Figura 1 com o devido cuidado verá que temos três quadrados mágicos, onde as somas das linhas, colunas e diagonais são 45 para o cateto X, 60 para cateto Y e 75 para a hipotenusa.

Examinando com mais cuida o leitor pode notar que o Teorema de Pitágoras impera nas relações entre estes três quadrados mágicos.

Se elevarmos ao quadrado o valor de qualquer uma das células do quadrado mágico da hipotenusa o resultado é igual à soma dos quadrados dos valores das células correspondentes ao cateto X e ao cateto Y.

Por exemplo, para a célula A1, no quadrado mágico da hipotenusa A1 = 40; no cateto X, A1 = 24 e no cateto Y, A1 = 32, então:

40²= 24² + 32² ? 1.600 = 576 + 1.024 ? 1.600 = 1.600

Isto ocorre também com o qualquer soma dos valores que compões determinada linha, coluna ou diagonal, como foi dito anteriormente a soma dos valores são 45 para o cateto X, 60 para cateto Y e 75 para a hipotenusa, logo:

75²= 45² + 60² ? 5.625 = 2.025 + 3.600 ? 5.625 = 5.625

Da mesma forma se elevar ao quadrado a soma dos valores de duas células de qualquer linha, coluna ou diagonal do quadrado mágico da hipotenusa é igual ao quadrado da soma das respectivas células dos quadrados mágicos do cateto X e do cateto Y.

Por exemplo, para as células A1 e C3, no quadrado mágico da hipotenusa A1 = 40 e C3 = 10; no cateto X, A1 = 24 e C3 = 6 e no cateto Y, A1 = 32 e C3 = 8, então:

(40 + 10)² = (24 + 6)² + (32 + 8)² ?

? 50² = 30² + 40² ? 2.500 = 900 + 1.600 ? 2.500 = 2.500 (V)

Outro exemplo, para as células B1 e B2, no quadrado mágico da hipotenusa B1 = 5 e B2 = 25; no cateto X, B1 = 3 e B2 = 15 e no cateto Y, B1 = 4 e B2 = 20, então:

(5 + 25)² = (3 + 15)² + (4 + 20)² ?

? 30² = 18² + 24² ? 900 = 324 + 576? 900 = 900 (V)

Além disso, note que a soma de todos os valores do quadrado mágico do cateto X é 135, do cateto Y é 180 e da hipotenusa é 225, então aplicando o Teorema de Pitágoras:

225²= 135² + 180² ? 50.625 = 18.225 + 32.400? 50.625 = 50.625 (V)

Fonte: HEATH, Royal V. Mathemagic: Magic, Puzzles and Games with Numbers (Dover Recreational Math) Paperback ? June 1, 1953.

- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...

- Trigonometria No Triângulo Retângulo
Trigonometria no Triângulo Retângulo Marcos Noé Relações trigonométricas no triângulo retânguloA trigonometria surgiu diante da necessidade do homem de calcular medidas com base em ângulos. Os estudos relacionados aos triângulos...

- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...

- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...

- Distância Entre Dois Pontos
Os estudos em Geometria Analítica possibilitam a relação entre a álgebra e a geometria, abrangendo situações em que são envolvidos ponto, reta e figuras espaciais. Um conceito básico de geometria deve ser aproveitado na GA, a fim de estabelecer...

Matemática