Matemática
Tipos particulares de funções
FUNÇÃO CONSTANTE
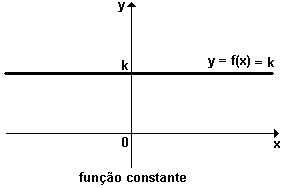
Uma função é dita constante quando é do tipo f(x) = k, onde k não depende de x .
Exemplos:
a) f(x) = 5
b) f(x) = -3
Nota : o gráfico de uma função constante é uma reta paralela ao eixo dos x .
Veja o gráfico a seguir:
FUNÇÃO DO 1º GRAU
Uma função é dita do 1º grau , quando é do tipo y = ax + b , onde a ¹ 0 .
Exemplos :
f(x) = 3x + 12 ( a = 3 ; b = 12 )
f(x) = -3x + 1 (a = -3; b = 1).
Propriedades da função do 1º grau :
1) o gráfico de uma função do 1º grau é sempre uma reta .
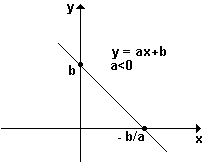
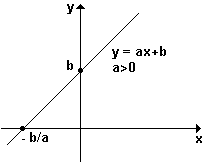
2) na função f(x) = ax + b , se b = 0 , f é dita função linear e se b ¹ 0 f é dita função afim .
Nota: consta que o termo AFIM foi introduzido por Leonhard Euler (pronuncia-se óiler) - excepcional matemático suíço - 1701/1783).
3) o gráfico intercepta o eixo dos x na raiz da equação f(x) = 0 e, portanto, no ponto de
abcissa x = - b/a .
4) o gráfico intercepta o eixo dos y no ponto (0 , b) , onde b é chamado coeficiente linear .
5) o valor a é chamado coeficiente angular e dá a inclinação da reta .
6) se a > 0 , então f é crescente .
7) se a < 0 , então f é decrescente .
8) quando a função é linear, ou seja, y = f(x) = ax , o gráfico é uma reta que sempre passa na origem.
Exercício resolvido:
1 - Determine a função f(x) = ax + b, sabendo-se que f(2) = 5 e f(3) = -10.
SOLUÇÃO: Podemos escrever:
5 = 2.a + b
-10 = 3.a + b
Subtraindo membro a membro, vem:
5 - (- 10) = 2.a + b - (3.a + b)
15 = - a \ a = - 15
Substituindo o valor de a na primeira equação (poderia ser na segunda), fica:
5 = 2.(- 15) + b \ b = 35.
Logo, a função procurada é: y = - 15x + 35.
Agora resolva esta: A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos afirmar que f(1) é
igual a:
*a) 2
b) -2
c) 0
d) 3
e) -3
FUNÇÃO DO 2º GRAU
Uma função é dita do 2º grau quando é do tipo f(x) = ax2 + bx + c , com a ¹ 0 .
Exemplos: f(x) = x2 - 2x + 1 ( a = 1 , b = -2 , c = 1 ) ;
y = - x2 ( a = -1 , b = 0 , c = 0 )
Gráfico da função do 2º grau y = ax2 + bx + c : é sempre uma parábola de eixo vertical .
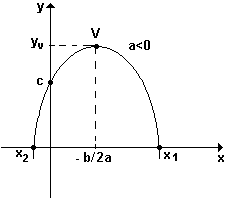
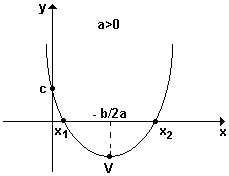
Propriedades do gráfico de y = ax2 + bx + c :
1) se a > 0 a parábola tem um ponto de mínimo .
2) se a < 0 a parábola tem um ponto de máximo
3) o vértice da parábola é o ponto V(xv , yv) onde:
xv = - b/2a
yv = - D /4a , onde D = b2 - 4ac
4) a parábola intercepta o eixo dos x nos pontos de abcissas x' e x'' , que são as raízes da
equação ax2 + bx + c = 0 .
5) a parábola intercepta o eixo dos y no ponto (0 , c) .
6) o eixo de simetria da parábola é uma reta vertical de equação x = - b/2a.
7) ymax = - D / 4a ( a < 0 )
8) ymin = - D /4a ( a > 0 )
9) Im(f) = { y Î R ; y ³ - D /4a } ( a > 0 )
10) Im(f) = { y Î R ; y £ - D /4a} ( a < 0)
11) Forma fatorada : sendo x1 e x2 as raízes da de f(x) = ax2 + bx + c , então ela pode ser escrita na forma fatorada a seguir :
y = a(x - x1).(x - x2)
Exercícios Resolvidos
1 - UCSal - Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto
(-1 , 8) pertence ao gráfico dessa função, então:
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor máximo é 0,25
d) o seu valor mínimo é 12,5
*e) o seu valor máximo é 12,5.
SOLUÇÃO: Sabemos que a função quadrática, pode ser escrita na forma fatorada:
y = a(x - x1)(x - x2) , onde x1 e x2, são os zeros ou raízes da função.
Portanto, poderemos escrever:
y = a[x - (- 2 )](x - 3) = a(x + 2)(x - 3)
y = a(x + 2)(x - 3)
Como o ponto (-1,8) pertence ao gráfico da função, vem:
8 = a(-1 + 2)(-1 - 3)
8 = a(1)(-4) = - 4.a
Daí vem: a = - 2
A função é, então: y = -2(x + 2)(x - 3) , ou y = (-2x -4)(x - 3)
y = -2x2 + 6x - 4x + 12
y = -2x2 + 2x + 12
Temos então: a = -2 , b = 2 e c = 12.
Como a é negativo, concluímos que a função possui um valor máximo.
Isto já elimina as alternativas B e D.
Vamos então, calcular o valor máximo da função.
D = b2 - 4ac = 22 - 4 .(-2).12 = 4+96 = 100
Portanto, yv = - 100/4(-2) = 100/8 = 12,5
Logo, a alternativa correta é a letra E.
2 - Que número excede o seu quadrado o máximo possível?
*a) 1/2
b) 2
c) 1
d) 4
e) -1/2
SOLUÇÃO: Seja x o número procurado.
O quadrado de x é x2 .
O número x excede o seu quadrado , logo: x - x2.
Ora, a expressão anterior é uma função quadrática y = x - x2 .
Podemos escrever:
y = - x2 + x onde a = -1, b = 1 e c = 0.
O valor procurado de x, será o xv (abcissa do vértice da função).
Assim,
xv = - b / 2.a = - 1 / 2(-1) = 1 / 2
Logo, a alternativa correta é a letra A .
Agora resolva estes similares:
1 - A diferença entre dois números é 8. Para que o produto seja o menor possível, um deles deve ser:
a) 16
b) 8
*c) 4
d) -4
e) -16
2 - A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:
a) 16
b) 8
c) 4
d) -4
*e) -16
- Função Do 2º Grau
4. VÉRTICE DE UMA PARÁBOLA É o ponto de maior ou menor valor que a função y = ax2 + bx + c pode atingir e coincide com a intersecção do eixo de simetria com o gráfico: Observação: eixo de simetria (R) é uma reta que divide a parábola em duas...
- Função 2º Grau
4. VÉRTICE DE UMA PARÁBOLA É o ponto de maior ou menor valor que a função y = ax2 + bx + c pode atingir e coincide com a intersecção do eixo de simetria com o gráfico: Observação: eixo de simetria (R) é uma reta que divide a parábola em duas...
- Coordenadas Do Vértice Da Parábola
Coordenadas do vértice da parábolaMarcelo Rigonatto VérticesToda função quadrática ou do 2º grau é do tipo f(x) = ax2 + bx + c, com a ≠ 0. O gráfico de uma função do segundo grau é uma parábola que, dependendo do...
- Função Afim
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é: O gráfico de uma função afim é uma reta não perpendicular...
- Função Afim
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é: O gráfico de uma função afim é uma reta não perpendicular...
Matemática
Tipos particulares de funções
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.comTipos particulares de funções
FUNÇÃO CONSTANTE
Uma função é dita constante quando é do tipo f(x) = k, onde k não depende de x .
Exemplos:
a) f(x) = 5
b) f(x) = -3
Nota : o gráfico de uma função constante é uma reta paralela ao eixo dos x .
Veja o gráfico a seguir:

FUNÇÃO DO 1º GRAU
Uma função é dita do 1º grau , quando é do tipo y = ax + b , onde a ¹ 0 .
Exemplos :
f(x) = 3x + 12 ( a = 3 ; b = 12 )
f(x) = -3x + 1 (a = -3; b = 1).
Propriedades da função do 1º grau :
1) o gráfico de uma função do 1º grau é sempre uma reta .
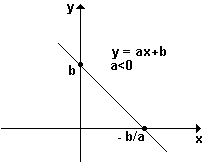
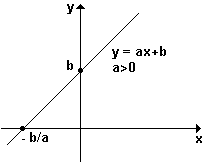
2) na função f(x) = ax + b , se b = 0 , f é dita função linear e se b ¹ 0 f é dita função afim .
Nota: consta que o termo AFIM foi introduzido por Leonhard Euler (pronuncia-se óiler) - excepcional matemático suíço - 1701/1783).
3) o gráfico intercepta o eixo dos x na raiz da equação f(x) = 0 e, portanto, no ponto de
abcissa x = - b/a .
4) o gráfico intercepta o eixo dos y no ponto (0 , b) , onde b é chamado coeficiente linear .
5) o valor a é chamado coeficiente angular e dá a inclinação da reta .
6) se a > 0 , então f é crescente .
7) se a < 0 , então f é decrescente .
8) quando a função é linear, ou seja, y = f(x) = ax , o gráfico é uma reta que sempre passa na origem.
Exercício resolvido:
1 - Determine a função f(x) = ax + b, sabendo-se que f(2) = 5 e f(3) = -10.
SOLUÇÃO: Podemos escrever:
5 = 2.a + b
-10 = 3.a + b
Subtraindo membro a membro, vem:
5 - (- 10) = 2.a + b - (3.a + b)
15 = - a \ a = - 15
Substituindo o valor de a na primeira equação (poderia ser na segunda), fica:
5 = 2.(- 15) + b \ b = 35.
Logo, a função procurada é: y = - 15x + 35.
Agora resolva esta: A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos afirmar que f(1) é
igual a:
*a) 2
b) -2
c) 0
d) 3
e) -3
FUNÇÃO DO 2º GRAU
Uma função é dita do 2º grau quando é do tipo f(x) = ax2 + bx + c , com a ¹ 0 .
Exemplos: f(x) = x2 - 2x + 1 ( a = 1 , b = -2 , c = 1 ) ;
y = - x2 ( a = -1 , b = 0 , c = 0 )
Gráfico da função do 2º grau y = ax2 + bx + c : é sempre uma parábola de eixo vertical .

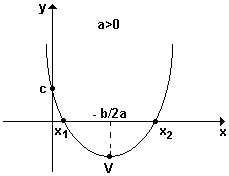
Propriedades do gráfico de y = ax2 + bx + c :
1) se a > 0 a parábola tem um ponto de mínimo .
2) se a < 0 a parábola tem um ponto de máximo
3) o vértice da parábola é o ponto V(xv , yv) onde:
xv = - b/2a
yv = - D /4a , onde D = b2 - 4ac
4) a parábola intercepta o eixo dos x nos pontos de abcissas x' e x'' , que são as raízes da
equação ax2 + bx + c = 0 .
5) a parábola intercepta o eixo dos y no ponto (0 , c) .
6) o eixo de simetria da parábola é uma reta vertical de equação x = - b/2a.
7) ymax = - D / 4a ( a < 0 )
8) ymin = - D /4a ( a > 0 )
9) Im(f) = { y Î R ; y ³ - D /4a } ( a > 0 )
10) Im(f) = { y Î R ; y £ - D /4a} ( a < 0)
11) Forma fatorada : sendo x1 e x2 as raízes da de f(x) = ax2 + bx + c , então ela pode ser escrita na forma fatorada a seguir :
y = a(x - x1).(x - x2)
Exercícios Resolvidos
1 - UCSal - Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto
(-1 , 8) pertence ao gráfico dessa função, então:
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor máximo é 0,25
d) o seu valor mínimo é 12,5
*e) o seu valor máximo é 12,5.
SOLUÇÃO: Sabemos que a função quadrática, pode ser escrita na forma fatorada:
y = a(x - x1)(x - x2) , onde x1 e x2, são os zeros ou raízes da função.
Portanto, poderemos escrever:
y = a[x - (- 2 )](x - 3) = a(x + 2)(x - 3)
y = a(x + 2)(x - 3)
Como o ponto (-1,8) pertence ao gráfico da função, vem:
8 = a(-1 + 2)(-1 - 3)
8 = a(1)(-4) = - 4.a
Daí vem: a = - 2
A função é, então: y = -2(x + 2)(x - 3) , ou y = (-2x -4)(x - 3)
y = -2x2 + 6x - 4x + 12
y = -2x2 + 2x + 12
Temos então: a = -2 , b = 2 e c = 12.
Como a é negativo, concluímos que a função possui um valor máximo.
Isto já elimina as alternativas B e D.
Vamos então, calcular o valor máximo da função.
D = b2 - 4ac = 22 - 4 .(-2).12 = 4+96 = 100
Portanto, yv = - 100/4(-2) = 100/8 = 12,5
Logo, a alternativa correta é a letra E.
2 - Que número excede o seu quadrado o máximo possível?
*a) 1/2
b) 2
c) 1
d) 4
e) -1/2
SOLUÇÃO: Seja x o número procurado.
O quadrado de x é x2 .
O número x excede o seu quadrado , logo: x - x2.
Ora, a expressão anterior é uma função quadrática y = x - x2 .
Podemos escrever:
y = - x2 + x onde a = -1, b = 1 e c = 0.
O valor procurado de x, será o xv (abcissa do vértice da função).
Assim,
xv = - b / 2.a = - 1 / 2(-1) = 1 / 2
Logo, a alternativa correta é a letra A .
Agora resolva estes similares:
1 - A diferença entre dois números é 8. Para que o produto seja o menor possível, um deles deve ser:
a) 16
b) 8
*c) 4
d) -4
e) -16
2 - A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:
a) 16
b) 8
c) 4
d) -4
*e) -16
- Função Do 2º Grau
4. VÉRTICE DE UMA PARÁBOLA É o ponto de maior ou menor valor que a função y = ax2 + bx + c pode atingir e coincide com a intersecção do eixo de simetria com o gráfico: Observação: eixo de simetria (R) é uma reta que divide a parábola em duas...
- Função 2º Grau
4. VÉRTICE DE UMA PARÁBOLA É o ponto de maior ou menor valor que a função y = ax2 + bx + c pode atingir e coincide com a intersecção do eixo de simetria com o gráfico: Observação: eixo de simetria (R) é uma reta que divide a parábola em duas...
- Coordenadas Do Vértice Da Parábola
Coordenadas do vértice da parábolaMarcelo Rigonatto VérticesToda função quadrática ou do 2º grau é do tipo f(x) = ax2 + bx + c, com a ≠ 0. O gráfico de uma função do segundo grau é uma parábola que, dependendo do...
- Função Afim
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é: O gráfico de uma função afim é uma reta não perpendicular...
- Função Afim
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é: O gráfico de uma função afim é uma reta não perpendicular...
