Matemática
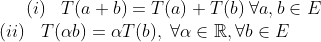
 : Se (ii) vale, então, dado
: Se (ii) vale, então, dado  , existe
, existe  tal que
tal que  . Mas, como T é linear, dado y = Ax, |x| < r, então |Ty| < C. Ou seja, leva uma bola B(0;A) em uma outra bola B(0;C).
. Mas, como T é linear, dado y = Ax, |x| < r, então |Ty| < C. Ou seja, leva uma bola B(0;A) em uma outra bola B(0;C).
 : Se T é limitada, então T(B(0;1)) está contido em B(0;A), para alguma A > 0. Mas isto equivale, pela linearidade de T, que, se |x| < r, então temos que |Tx| < rA. Daí vemos claramente que T deve ser contínua no zero.
: Se T é limitada, então T(B(0;1)) está contido em B(0;A), para alguma A > 0. Mas isto equivale, pela linearidade de T, que, se |x| < r, então temos que |Tx| < rA. Daí vemos claramente que T deve ser contínua no zero. 

- Baixar - Álgebra Linear ? Boldrini
Título: Álgebra Linear Autor: Boldrini Editora: HARBRA Idioma: Português Número de páginas: 411 Edição: 3 Tamanho: 9.1 Mb Visto que os alunos que cursam pela primeira vez esta disciplina frequentemente a julgam muito abstrata e não veem como...
- Análise Funcional - Parte Iv: Mais Sobre Espaços De Hilbert.
Na continuação da nossa jornada pelo mundo dos espaços de Hilbert, analisemos mais um ponto de contato entre a teoria dos Espaços de Hilbert e a teoria de Espaços Vetoriais de Dimensão Finita. Esta conexão entre a Álgebra Linear e a Análise Funcional...
- Análise Funcional - Parte Iii: Introdução Aos Espaços De Hilbert
Hoje vamos falar um pouco da imensa teoria existente sobre espaços de Hilbert. Quando se fala em Análise Funcional, talvez este seja o caso particular mais interessante de um Espaço de Banach, pois, além de obtermos informações sobre operadores...
- Equações Funcionais - Equação De Cauchy
Hoje vamos falar de um dos conceitos primordiais da teoria de Equações Funcionais, que é a equação de Cauchy. De fato, a Equação de Cauchy generaliza o conceito de operador linear: Se T for um operador linear definido na reta...
- Análise Funcional - Parte Ii: O Teorema De Baire E O Princípio Da Limitação Uniforme
Vamos falar hoje de uma ferramenta muito poderosa quando trabalhamos com espaços métricos, que vai originar um teorema muito importante e utilizado na Análise Funcional: o Princípio da Limitação Uniforme, ou o Teorema de Banach-Steinhaus. Estamos...
Matemática
Transformações Lineares em Espaços de Dimensão Infinita - Parte I
Hoje vamos falar de Transformações Lineares, com um foco específico nas transformações onde o espaço domínio (aqui sempre tratado como E) tem dimensão infinita. Um espaço vetorial nada mais é que um conjunto fechado por somas e por multiplicação por escalares (reais ou complexos, dependendo do caso), e a dimensão do espaço vetorial é definida como a cardinalidade da base deste espaço.
(Aviso: ao leitor sem familiaridade com um pouco de álgebra linear ou análise em nível elementar, recomendamos que espere um pouco e leia o artigo depois de ter mais segurança nesses conceitos)
Uma transformação linear T entre espaços vetoriais E e F é definida como um mapa entre esses espaços satisfazendo
Quando o espaço E=F, dizemos que T é um operador linear, e quando F é o conjunto dos reais, dizemos que T é um funcional linear.
Comecemos com alguns teoremas básicos da teoria mais elementar das transformações lineares:
Proposição 1: Sejam E,F espaços vetoriais normados (isto é, cada um admite uma norma). Então são equivalentes:
(i) é contínua
é contínua
(ii)  é contínua em um ponto.
é contínua em um ponto.
(iii)  é limitada (isto é, leva conjuntos limitados em conjuntos limitados)
é limitada (isto é, leva conjuntos limitados em conjuntos limitados)
Demonstração:  : Se (i) vale, obviamente vale (ii). Se T é contínua em um ponto y de E, então, dada
: Se (i) vale, obviamente vale (ii). Se T é contínua em um ponto y de E, então, dada  , temos que
, temos que  . Suponhamos que temos um outro x em E e uma sequência
. Suponhamos que temos um outro x em E e uma sequência  . Como a sequência
. Como a sequência  , então
, então  . Mas isto equivale a
. Mas isto equivale a  , e assim T é contínua em todo o E.
, e assim T é contínua em todo o E.
Corolário 1: Se E tem dimensão finita, então toda transformação linear de E em F é contínua.
Demonstração: Basta mostrar que T como acima é limitada, pela Prop. 1. Mas isto é fácil: Seja  uma base de E com cada um dos elementos tendo norma 1. Como um espaço de dimensão finita k é isomorfo ao
uma base de E com cada um dos elementos tendo norma 1. Como um espaço de dimensão finita k é isomorfo ao  , podemos considerar a norma do máximo em
, podemos considerar a norma do máximo em  como a norma de E. Assim, se |x| é menor ou igual a 1 em E,
como a norma de E. Assim, se |x| é menor ou igual a 1 em E,  . Logo, T é limitada, e, então, contínua.
. Logo, T é limitada, e, então, contínua. 
Vamos construir um exemplo onde E tem dimensão infinita, para obter um funcional T não contínuo em E.
Seja E o espaço vetorial das sequências onde todos menos um número finito de termos é zero. Se
o conjunto desses elementos forma uma base de E. Além disso, se definirmos um funcional nos elementos de uma base, definimo-no em todo o espaço. Logo, defina T como  . Considerando no espaço E a norma dada pela soma dos módulos dos termos da sequência, então todos os termos acima definidos têm norma 1, e, portanto, T não é limitada neste conjunto, que obviamente é limitado. Logo, T não pode ser contínua.
. Considerando no espaço E a norma dada pela soma dos módulos dos termos da sequência, então todos os termos acima definidos têm norma 1, e, portanto, T não é limitada neste conjunto, que obviamente é limitado. Logo, T não pode ser contínua.
Para finalizar esta primeira parte, vejamos um resultado importante:
Definição 1: Um espaço vetorial normado é dito um espaço de Banach se, dada uma sequência  de Cauchy, então esta sequência é convergente, ou seja, existe
de Cauchy, então esta sequência é convergente, ou seja, existe  .
.
Definição 2: Dados E,F espaços vetoriais normados, defina L(E;F) como o espaço dos mapas lineares limitados (contínuos) de E em F.
Proposição 2: Se F é um espaço de Banach, L(E;F) também o é.
Demonstração: Exercício. (Dica: Use que F é Banach para achar a T desejada como limite pontual, e aí use a limitação para provar que T é contínua e que a sequência de fato converge a T)
- Baixar - Álgebra Linear ? Boldrini
Título: Álgebra Linear Autor: Boldrini Editora: HARBRA Idioma: Português Número de páginas: 411 Edição: 3 Tamanho: 9.1 Mb Visto que os alunos que cursam pela primeira vez esta disciplina frequentemente a julgam muito abstrata e não veem como...
- Análise Funcional - Parte Iv: Mais Sobre Espaços De Hilbert.
Na continuação da nossa jornada pelo mundo dos espaços de Hilbert, analisemos mais um ponto de contato entre a teoria dos Espaços de Hilbert e a teoria de Espaços Vetoriais de Dimensão Finita. Esta conexão entre a Álgebra Linear e a Análise Funcional...
- Análise Funcional - Parte Iii: Introdução Aos Espaços De Hilbert
Hoje vamos falar um pouco da imensa teoria existente sobre espaços de Hilbert. Quando se fala em Análise Funcional, talvez este seja o caso particular mais interessante de um Espaço de Banach, pois, além de obtermos informações sobre operadores...
- Equações Funcionais - Equação De Cauchy
Hoje vamos falar de um dos conceitos primordiais da teoria de Equações Funcionais, que é a equação de Cauchy. De fato, a Equação de Cauchy generaliza o conceito de operador linear: Se T for um operador linear definido na reta...
- Análise Funcional - Parte Ii: O Teorema De Baire E O Princípio Da Limitação Uniforme
Vamos falar hoje de uma ferramenta muito poderosa quando trabalhamos com espaços métricos, que vai originar um teorema muito importante e utilizado na Análise Funcional: o Princípio da Limitação Uniforme, ou o Teorema de Banach-Steinhaus. Estamos...
