Matemática
RAZÕES TRIGONOMÉTRICAS DOS ÂNGULOS DE 30º, 45º E 60º
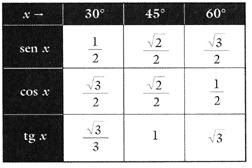
Podemos resumir os valores para o seno, co-seno e tangente dos ângulos de 30º, 45º e 60º em uma única tabela. Tais valores serão usados freqüentemente daqui em diante.
Aplicação
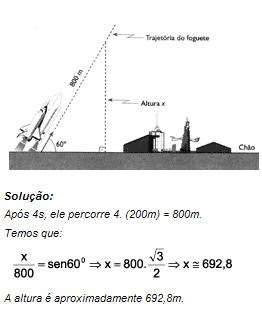
Um foguete é lançado a 200m/s, segundo um ângulo de inclinação de 60º (ver figura). Determinar a altura do foguete após 4s, supondo a trajetória retilínea e a velocidade constante.
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida).
1. RAZÕES TRIGONOMÉTRICAS
O triângulo é retângulo quando um de seus ângulos internos é reto, ou seja, mede 90°.
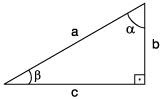
Observe-se o triângulo ABC da figura com  = 90° (reto), e seus ângulos agudos e .
É importante saber que:
a) Em relação ao ângulo , temos:
c é o cateto oposto;
b é o cateto adjacente.
b) Em relação ao ângulo , temos:
b é o cateto oposto;
c é o cateto adjacente.
Seno, co-seno e tangente de um ângulo agudo
Seja a medida de um ângulo agudo do triângulo acima, temos:
a) Seno do ângulo (sen ):
É a razão entre a medida do cateto oposto a e a medida da hipotenusa, ou seja:
b) Co-seno do ângulo (cos ):
É a razão entre a medida do cateto adjacente a e a medida da hipotenusa, isto é:

Aplicação
Calcular x, dados:
sen = 0,8; cos = 0,6; tg = 0,75
Solução:
Primeiro é preciso decidir qual das três razões trigonométricas dadas convém ao problema.
Observe que a hipotenusa é conhecida e que x é a medida do cateto adjacente a . Como hipotenusa e cateto adjacente são relacionados pelo co-seno, temos:
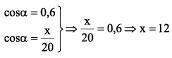



Fórmulas da Adição
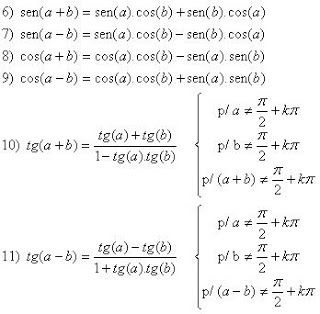
As fórmulas acima são verdadeiras para arcos positivos, cujo a soma pertence ao primeiro quadrante.
Fórmulas da Multiplicação
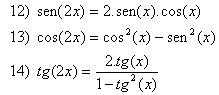
2. ARCO DUPLO
Usaremos as fórmulas da soma e da subtração de dois arcos para obter as fórmulas do arco duplo.
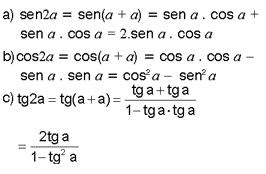
Aplicação

3. TRANSFORMAÇÃO EM PRODUTO
As fórmulas de adição e subtração de arcos podem ser transformadas em produtos a partir de:

plicação
Transformar em produto a expressão y = sen 40° + sen 30°.
Solução:
m = 40° e n = 30°
Aplicando a forma fatorada de sen m + sen n, temos:
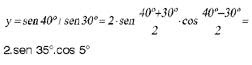
4. EQUAÇÕES TRIGONOMÉTRICAS
É toda equação em que figura uma função trigonométrica com arco desconhecido. Chamam-se soluções de uma equação trigonométrica os valores da variável, caso existam, que satisfazem a equação dada.
Exemplos:
a) sen x = – 1
b) cos x = 0
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas.
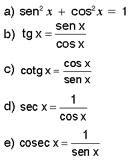
Observações:
a) cotg x = co-tangente de x
b) sec x = secante de x
c) cosec x = co-ssecante de x
Aplicação
Simplificar a expressão:
1 – sen x . cos x . tg

Aplicação
Calcular sen 75°.
Solução:
Podemos observar que 75º = 30º + 45º; logo sen 75º = sen (30º + 45º). A partir da fórmula, temos:
sen (30º + 45º) = sen 30º. cos 45º + sen 45º . cos 30º =
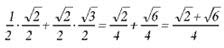
www.colegioweb.com.br
- Lei Dos Senos
Os estudos trigonométricos no triângulo retângulo têm por finalidade relacionar os ângulos do triângulo com as medidas dos lados, por meio das seguintes relações: seno, cosseno e tangente. Essas relações utilizam o cateto oposto, o cateto adjacente...
- Razões Trigonométricas
Catetos e Hipotenusa Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos. Observe a figura: Seno, Cosseno e TangenteConsidere um triângulo retângulo BAC: Tomando por base os elementos desse triângulo,...
- Trigonometria No Triângulo Retângulo
Trigonometria no Triângulo Retângulo Marcos Noé Relações trigonométricas no triângulo retânguloA trigonometria surgiu diante da necessidade do homem de calcular medidas com base em ângulos. Os estudos relacionados aos triângulos...
- Relações Trigonométricas No Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
Matemática
Trigonométria
RAZÕES TRIGONOMÉTRICAS DOS ÂNGULOS DE 30º, 45º E 60º
Podemos resumir os valores para o seno, co-seno e tangente dos ângulos de 30º, 45º e 60º em uma única tabela. Tais valores serão usados freqüentemente daqui em diante.

Aplicação
Um foguete é lançado a 200m/s, segundo um ângulo de inclinação de 60º (ver figura). Determinar a altura do foguete após 4s, supondo a trajetória retilínea e a velocidade constante.

TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida).
1. RAZÕES TRIGONOMÉTRICAS
O triângulo é retângulo quando um de seus ângulos internos é reto, ou seja, mede 90°.
Observe-se o triângulo ABC da figura com  = 90° (reto), e seus ângulos agudos e .

É importante saber que:
a) Em relação ao ângulo , temos:
c é o cateto oposto;
b é o cateto adjacente.
b) Em relação ao ângulo , temos:
b é o cateto oposto;
c é o cateto adjacente.
Seno, co-seno e tangente de um ângulo agudo
Seja a medida de um ângulo agudo do triângulo acima, temos:
a) Seno do ângulo (sen ):
É a razão entre a medida do cateto oposto a e a medida da hipotenusa, ou seja:
b) Co-seno do ângulo (cos ):
É a razão entre a medida do cateto adjacente a e a medida da hipotenusa, isto é:

Aplicação
Calcular x, dados:
sen = 0,8; cos = 0,6; tg = 0,75
Solução:
Primeiro é preciso decidir qual das três razões trigonométricas dadas convém ao problema.
Observe que a hipotenusa é conhecida e que x é a medida do cateto adjacente a . Como hipotenusa e cateto adjacente são relacionados pelo co-seno, temos:
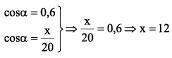



Fórmulas da Adição
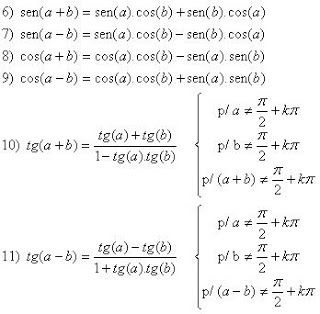
As fórmulas acima são verdadeiras para arcos positivos, cujo a soma pertence ao primeiro quadrante.
Fórmulas da Multiplicação
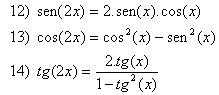
2. ARCO DUPLO
Usaremos as fórmulas da soma e da subtração de dois arcos para obter as fórmulas do arco duplo.
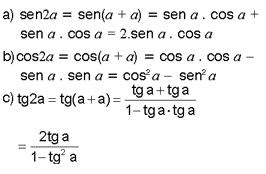
Aplicação

3. TRANSFORMAÇÃO EM PRODUTO
As fórmulas de adição e subtração de arcos podem ser transformadas em produtos a partir de:

plicação
Transformar em produto a expressão y = sen 40° + sen 30°.
Solução:
m = 40° e n = 30°
Aplicando a forma fatorada de sen m + sen n, temos:
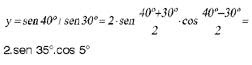
4. EQUAÇÕES TRIGONOMÉTRICAS
É toda equação em que figura uma função trigonométrica com arco desconhecido. Chamam-se soluções de uma equação trigonométrica os valores da variável, caso existam, que satisfazem a equação dada.
Exemplos:
a) sen x = – 1
b) cos x = 0
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas.
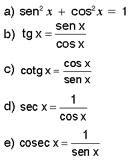
Observações:
a) cotg x = co-tangente de x
b) sec x = secante de x
c) cosec x = co-ssecante de x
Aplicação
Simplificar a expressão:
1 – sen x . cos x . tg

Aplicação
Calcular sen 75°.
Solução:
Podemos observar que 75º = 30º + 45º; logo sen 75º = sen (30º + 45º). A partir da fórmula, temos:
sen (30º + 45º) = sen 30º. cos 45º + sen 45º . cos 30º =
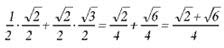
www.colegioweb.com.br
- Lei Dos Senos
Os estudos trigonométricos no triângulo retângulo têm por finalidade relacionar os ângulos do triângulo com as medidas dos lados, por meio das seguintes relações: seno, cosseno e tangente. Essas relações utilizam o cateto oposto, o cateto adjacente...
- Razões Trigonométricas
Catetos e Hipotenusa Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos. Observe a figura: Seno, Cosseno e TangenteConsidere um triângulo retângulo BAC: Tomando por base os elementos desse triângulo,...
- Trigonometria No Triângulo Retângulo
Trigonometria no Triângulo Retângulo Marcos Noé Relações trigonométricas no triângulo retânguloA trigonometria surgiu diante da necessidade do homem de calcular medidas com base em ângulos. Os estudos relacionados aos triângulos...
- Relações Trigonométricas No Triângulo Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
