Matemática

Um problema, várias soluções

O objetivo desta postagem é apresentar um problema muito interessante no que diz respeito à variedade de soluções possíveis. O enunciado do problema é o seguinte:

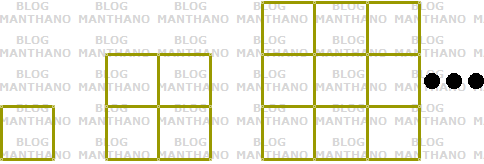
Tome muitas varetas, tais quais a representada na figura 1, e comece a construir algumas estruturas quadriculadas tais quais as representadas na figura 2.

Figura 1 - vareta

Figura 2 - estruturas quadriculadas construídas com as varetas

Observe que:

- na primeira construção, utilizamos 1 vareta como base do quadrado quadriculado construído;

- na segunda construção, utilizamos 2 varetas como base do quadrado quadriculado construído;

- na terceira construção, utilizamos 3 varetas como base do quadrado quadriculado construído.

Suponha que continuemos a construir tais quadrados quadriculados indefinidamente conforme o padrão sugerido pela figura 2. A pergunta é a seguinte:

Quantas varetas serão necessárias para construir o n-ésimo quadrado?

ou, de outro modo,

Quantas varetas serão necessárias na n-ésima construção?

ou ainda

Quantas varetas serão necessárias para construir o quadrado quadriculado cuja base possui n varetas?

Note que quando n = 2, então a resposta é 12. O problema pede uma resposta genérica, em função de n.

SOLUÇÃO 1 (usando teoria dos grafos):

Esta solução é a solução que originalmente apresentei quando, na faculdade, o problema me foi proposto:

Olhando para cada construção como um grafo, vemos que cada construção representa um grafo planar conexo. Logo a versão plana do teorema de Euler para poliedros convexos se aplica, ou seja, vale que

V + F ? A = 2 (#)

onde V representa o número de pontos em que há intersecção de varetas, F representa o número de regiões delimitadas por varetas (incluindo a exterior) e A representa o número de varetas. Os números V e F são fáceis de calcular se conhecermos quantas varetas há na base do quadrado. Assim, observando as figuras, podemos perceber que na n-ésima construção teremos:

V = (n + 1)²

F = n² + 1

Segue de (#) que

A = V + F ? 2 = (n + 1)² + n² + 1 ? 2 = 2n(n + 1)

Para maiores explicações sobre o que é um "grafo planar conexo", sugiro que o leitor viste esta postagem (acompanhando as continuações, o leitor poderá ainda compreender melhor o que diz o teorema acima utilizado bem como observar outra aplicação dele).

SOLUÇÃO 2 (usando teoria dos grafos, de novo!):

Esta segunda solução é uma que, mais uma vez, utiliza a linguagem da teoria dos grafos: como cada construção pode ser vista como um grafo planar conexo, vale que

SG = 2A (##)

onde SG representa a soma dos graus e A representa o número de varetas (veja aqui uma explicação para a expressão (##)).

Considere agora o n-ésimo grafo. Ele possui n² + 1 regiões, das quais uma é a exterior. A região exterior tem grau igual a 4n (quatro "lados", cada um com n varetas) enquanto que todas as outras n² regiões têm grau exatamente igual a 4. Assim, a partir de (##), concluímos que

A = SG/2 = (4n + 4n²)/2 = 2n(n + 1)

Para maiores esclarecimentos sobre grau e região de um grafo, novamente remeto o leitor a esta postagem.

Note que nas duas soluções acima chamamos de "vareta" aquilo que tecnicamente se chama "aresta".

SOLUÇÃO 3 (usando ???): desafio para o leitor!

SOLUÇÃO 4 (usando ???): desafio para o leitor!

SOLUÇÃO 5 (usando ???): desafio para o leitor!

As soluções 3, 4 e 5 não foram "descobertas" por mim. Elas me foram apresentadas na aula em que o problema foi proposto. Desafiamos, então, o leitor a descobrí-las e o convidamos a apresentá-la na área dos comentários.

Obs. 1: Em postagem posterior publicaremos as demais soluções, incluindo as possíveis soluções dos comentários dos leitores (o fato de eu ter deixado três soluções em branco indica que existem pelo menos mais três diferentes abordagens para este problema).

Obs. 2: eu categorizei esta postagem como Raciocínio Lógico pois acredito que a solução mais direta deste problema envolve mais uma "boa sacada" do que algum conhecimento muito específico.

Obs. 3: Veja outro problema com várias soluções no blog Fatos Matemáticos.

ATUALIZAÇÃO: confira aqui a continuação desta postagem, com as soluções prometidas.

Referência: notas de aula.
Erros podem ser relatados aqui.

- Aprenda A Fazer Vestibular Com O Método Pega-varetas
Lembra daquele jogo pega-varetas? Bastava lançar algumas varetas no chão e você tinha de pegar o máximo possível sem movimentar as outras varetas. A primeira coisa a fazer era sempre pegar aquelas que estavam mais fáceis, mesmo, para só depois...

- Alguns Exercícios Resolvidos De Álgebra Linear
A pedido de um leitor apresento, logo abaixo, soluções para algumas questões de Matemática da Prova 7 - Grupo F - Nível Superior - Área Ambiental - 2010 do PROMINP (Programa de Mobilização da Indústria Nacional de Petróleo...

- Solucionando O Problema Das 3 Casas Através Da Teoria Do Grafos - Final
[veja o problema aqui] [veja a 1ª parte da solução aqui] [veja a 2ª parte da solução aqui] Eis o desfecho da solução: Se cada região tem no mínimo grau 4 e se há 5 regiões, então a soma dos graus (SG) será no mínimo 5.4=20, logo o grafo...

- Solucionando O Problema Das 3 Casas Através Da Teoria Do Grafos - Parte 2
[veja o problema aqui] [veja a 1ª parte da solução aqui] Vamos então à solução. O texto dizia: ...deixamos os seguintes desafios para o leitor interessado e curioso: Achar a solução para o caso de duas casas ... Achar a solução...

- Solucionando O Problema Das 3 Casas Através Da Teoria Do Grafos - Parte 1
[veja o problema aqui] Este texto é uma introdução à solução que apresentaremos para o problema das três casas. O que é um grafo? Um grafo é um conjunto de pontos com linhas contínuas (retas ou não) que unem alguns desses pares de pontos....

Matemática