Matemática
O cilindro é um sólido geométrico classificado como corpo redondo por conter uma de suas faces arredondadas. Podemos observar a utilização do cilindro na indústria de embalagens, reservatórios de combustíveis e líquidos em geral. Em virtude da sua grande utilização no cotidiano, é importante conhecer seus elementos e saber realizar o cálculo de seu volume
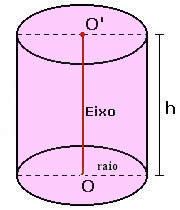Considere um cilindro circular reto de altura h e raio da base r. O volume do cilindro é obtido realizando o produto entre a área da base e a altura h. Ou seja,
r → o raio da base.
h → a altura do cilindro.
Vejamos alguns exemplos de aplicação da fórmula do volume do cilindro.
Exemplo 1. Considere um cilindro circular reto de 8 cm de altura e raio da base medindo 5 cm. Determine a capacidade desse cilindro. (Utilize π = 3,14)
Solução: De acordo com o enunciado do problema, temos que:
h = 8 cm
r = 5 cm
Calcular a capacidade é o mesmo que determinar o volume do cilindro.
Utilizando a fórmula do volume, obtemos:
V = π∙r2∙h
V = 3,14 ∙ 52∙8
V = 3,14 ∙ 25 ∙ 8
V = 628 cm3
Portanto, esse cilindro apresenta capacidade de 628 cm3.
Exemplo 2. Um reservatório de combustíveis apresenta o formato de um cilindro circular reto de 15 metros de diâmetro e 6 metros de altura. Determine a capacidade, em litros, desse reservatório. (Utilize π=3,14)
Solução: Temos que:
r = d/2 = 15/2 = 7,5 m
h = 6 m
Utilizando a fórmula do volume, obtemos:
V = π∙r2∙h
V = 3,14 ∙ (7,5)2 ∙ 6
V = 3,14 ∙ 56,25 ∙ 6
V = 1059,75 m3
O exercício quer a capacidade em litros. Devemos lembrar que:
1dm3 = 1 litro ou 1m3 = 1000 litros
Assim, o volume, em litros, desse reservatório será de:
V = 1059,75 ∙ 1000 = 1.059.750 litros
Exemplo 3. Uma indústria de embalagens deseja fabricar uma lata de tinta cilíndrica com raio da base medindo 5 cm de comprimento e com capacidade para 1 litro. Qual deverá ser o comprimento da altura dessa embalagem? (Use π = 3,1)
Solução: De acordo com o problema, o volume desse cilindro deverá ser de 1 litro ou 1 dm3. Sabemos que o raio da base será de 5 cm, que equivale a 0,5 dm. Utilizando a fórmula do volume, teremos:
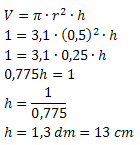
Portanto, a lata deverá ter uma altura de, aproximadamente, 13 cm.
- Questão 57 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
Um tonel de vinho tem a forma de um cilindro, cuja base interna tem 60 cm de raio e altura interna 0,8 m. É correto afirmar que a capacidade desse tonel é (A) menor que 500 litros. (B) maior ou igual a 500 litros e menor que 750 litros. (C) maior...
- Seção Meridiana E Cilindro Equilátero
Seção Meridiana e Cilindro Eqüilátero Seção meridiana de um cilindro circular reto é a interseção deste com um plano que contém o eixo. A seção meridiana de um cilindro reto é um retângulo. Aplicação (Mack–SP) Um cilindro tem área...
- Cilindro
O cilindro é um corpo redondo com duas bases opostas e paralelas. Podem ser classificados, de acordo com a inclinação da geratriz em relação aos planos das bases, em: cilindro circular oblíquo (a geratriz é oblíqua às bases) e cilindro circular...
- Área Total Do Cilindro
CilindrosO cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas faces arredondadas. Em razão dessa característica, o cálculo...
- Área Total Do Cilindro
Área total do cilindroMarcelo Rigonatto CilindrosO cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas...
Matemática
Volume do cilindro
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Volume do cilindro
Marcelo Rigonatto Cilindro
V = (área da base) × (altura)
Como a base do cilindro é uma circunferência de raio r, temos que:(área da base) = π∙r2
Sabemos que a altura do cilindro é h. Assim, a fórmula para o cálculo do volume do cilindro é dada por:V = π∙r2∙h
Sendor → o raio da base.
h → a altura do cilindro.
Vejamos alguns exemplos de aplicação da fórmula do volume do cilindro.
Exemplo 1. Considere um cilindro circular reto de 8 cm de altura e raio da base medindo 5 cm. Determine a capacidade desse cilindro. (Utilize π = 3,14)
Solução: De acordo com o enunciado do problema, temos que:
h = 8 cm
r = 5 cm
Calcular a capacidade é o mesmo que determinar o volume do cilindro.
Utilizando a fórmula do volume, obtemos:
V = π∙r2∙h
V = 3,14 ∙ 52∙8
V = 3,14 ∙ 25 ∙ 8
V = 628 cm3
Portanto, esse cilindro apresenta capacidade de 628 cm3.
Exemplo 2. Um reservatório de combustíveis apresenta o formato de um cilindro circular reto de 15 metros de diâmetro e 6 metros de altura. Determine a capacidade, em litros, desse reservatório. (Utilize π=3,14)
Solução: Temos que:
r = d/2 = 15/2 = 7,5 m
h = 6 m
Utilizando a fórmula do volume, obtemos:
V = π∙r2∙h
V = 3,14 ∙ (7,5)2 ∙ 6
V = 3,14 ∙ 56,25 ∙ 6
V = 1059,75 m3
O exercício quer a capacidade em litros. Devemos lembrar que:
1dm3 = 1 litro ou 1m3 = 1000 litros
Assim, o volume, em litros, desse reservatório será de:
V = 1059,75 ∙ 1000 = 1.059.750 litros
Exemplo 3. Uma indústria de embalagens deseja fabricar uma lata de tinta cilíndrica com raio da base medindo 5 cm de comprimento e com capacidade para 1 litro. Qual deverá ser o comprimento da altura dessa embalagem? (Use π = 3,1)
Solução: De acordo com o problema, o volume desse cilindro deverá ser de 1 litro ou 1 dm3. Sabemos que o raio da base será de 5 cm, que equivale a 0,5 dm. Utilizando a fórmula do volume, teremos:
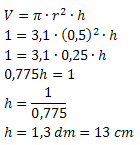
Portanto, a lata deverá ter uma altura de, aproximadamente, 13 cm.
- Questão 57 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
Um tonel de vinho tem a forma de um cilindro, cuja base interna tem 60 cm de raio e altura interna 0,8 m. É correto afirmar que a capacidade desse tonel é (A) menor que 500 litros. (B) maior ou igual a 500 litros e menor que 750 litros. (C) maior...
- Seção Meridiana E Cilindro Equilátero
Seção Meridiana e Cilindro Eqüilátero Seção meridiana de um cilindro circular reto é a interseção deste com um plano que contém o eixo. A seção meridiana de um cilindro reto é um retângulo. Aplicação (Mack–SP) Um cilindro tem área...
- Cilindro
O cilindro é um corpo redondo com duas bases opostas e paralelas. Podem ser classificados, de acordo com a inclinação da geratriz em relação aos planos das bases, em: cilindro circular oblíquo (a geratriz é oblíqua às bases) e cilindro circular...
- Área Total Do Cilindro
CilindrosO cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas faces arredondadas. Em razão dessa característica, o cálculo...
- Área Total Do Cilindro
Área total do cilindroMarcelo Rigonatto CilindrosO cilindro é um sólido geométrico bastante utilizado na indústria de embalagens e na armazenagem de líquidos em geral. É considerado um corpo redondo por conter uma de suas...