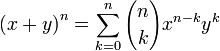Matemática
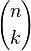 são chamados coeficientes binomiais e são definidos como:
são chamados coeficientes binomiais e são definidos como:
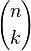 corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.
corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.


- Questão 9 ? Professor De Matemática ? Seap ? Paraná ? 2.013
Considere a seqüência an = logb1 ?5 + logb2 ?5 + ... + logbn ?5 onde b1 = a (a > 1) e bk+1 = ( bk )2 , k = 1 , ... , n ? 1. Determine o valor de a para o qual a10 =...
- ...::definição De Função Do 1º Grau E Zero De Uma Função Do 1º Grau::...
FUNÇÃO DO 1º GRAU Prof. Esp. Deivison da Silva e Silvae-mail:[email protected]...
- Post De Número 260
É com muita felicidade, que nós do Clave de Pi chgamos a marca de nosso post de numero 260. Agradecemos a todos que acessam nosso blog, pois sem vocês nada existiria. Também agradecemos a todos que comentam em nosso blog, aos nossos parceiros e todos...
- Termos Semelhantes
Dois ou mais termos são semelhantes quando têm a mesma parte literal.Exemplos:a) 5m e -7 m são termos semelhantesb) 2xy³ e 9y³x São termos semelhantesObs: veja que não...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...
Matemática
binômio de Newton
Notação e fórmula
O teorema do binômio de Newton se escreve como segue: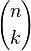 são chamados coeficientes binomiais e são definidos como:
são chamados coeficientes binomiais e são definidos como: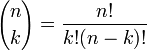 , onde
, onde 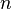 e
e 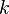 são inteiros,
são inteiros, 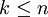 e
e 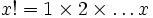 é o fatorial de x.
é o fatorial de x.
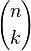 corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.
corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.A fórmula do binômio de Newton é a fórmula que dá o desenvolvimento de (x+y)n
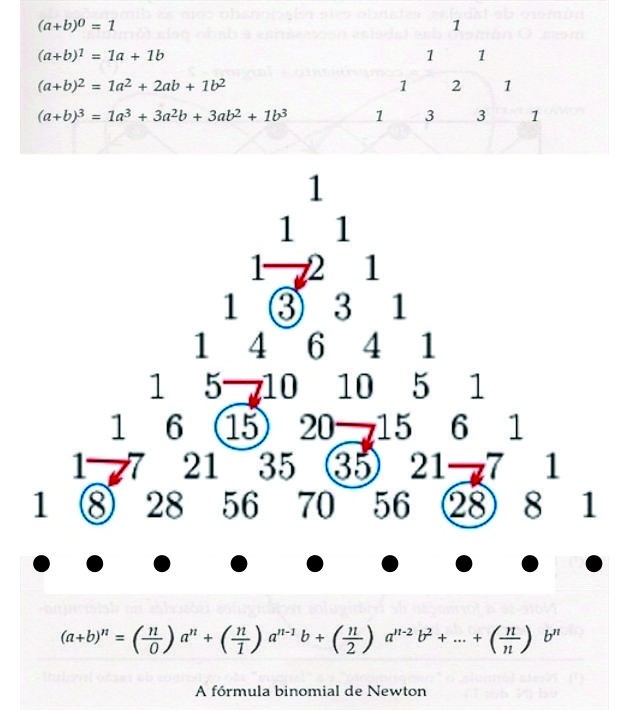
Desenvolvendo o binômio (x + y)n, n ? ?, encontramos: (x+y)n =

Toda potência da forma (x+y)n , com x,y ? ? e n ? ?, é conhecido como binômio de Newton. O desenvolvimento do binômio de Newton é simples em casos como os seguintes, que você já estudou no ensino fundamental.
Você aprendeu que:
a) (x+y)0 = 1 -1 termo.
b) (x+y)1 = 1x + 1y -2 termos.
c) (x+y)2 = 1x² + 2xy + 1y² -3 termos.
d) (x+y)3 = 1x3 + 3x2y+3xy2 +1y3 -4 termos.
e) (x+y)4 = ?
.
.
.
Um dos processos para determinar (x+y)4 é efetuar o produto (x+y)3 (x+y) que você já conhece e sabe que muita ?mão de obra?.
E se continuar aumentando o expoente do binômio. Como fica?
Em casos como (x+y)7 , (2x-y)5 , (x+2)10 e tantos outros, vamos recorrer à
análise combinatória.
análise combinatória.
Observe os exemplos:

-
O número de termos é dado pelo n+1 termos
- O n é o valor do expoente do binômio
- O expoente de x decresce de n até 0
- O expoente de y cresce de 0 até n.
- O desenvolvimento do binômio (x + y)n é um polinômio.
- O desenvolvimento de (x + y)n possui (n + 1) termos.
- Os coeficientes dos termos eqüidistantes dos extremos, no desenvolvimento de (x + y)n são iguais.
- A soma dos coeficientes de (x + y)n é igual a 2n.
Triângulo de Pascal e o binomio de Newton
Triângulo de Pascal e o binomio de Newton
A matemática tem a particularidade de relacionar ideias que, à primeira vista, parecem completamente independentes. É o que se passa com o triângulo de Pascal e com a fórmula binomial de Newton.
Cada linha do triângulo de Pascal representa os coeficientes do desenvolvimento de uma determinada potência do binómio (a+b).
REFERÊNCIAS:
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. ? A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. ? Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. ? A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. ? Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.
- Questão 9 ? Professor De Matemática ? Seap ? Paraná ? 2.013
Considere a seqüência an = logb1 ?5 + logb2 ?5 + ... + logbn ?5 onde b1 = a (a > 1) e bk+1 = ( bk )2 , k = 1 , ... , n ? 1. Determine o valor de a para o qual a10 =...
- ...::definição De Função Do 1º Grau E Zero De Uma Função Do 1º Grau::...
FUNÇÃO DO 1º GRAU Prof. Esp. Deivison da Silva e Silvae-mail:[email protected]...
- Post De Número 260
É com muita felicidade, que nós do Clave de Pi chgamos a marca de nosso post de numero 260. Agradecemos a todos que acessam nosso blog, pois sem vocês nada existiria. Também agradecemos a todos que comentam em nosso blog, aos nossos parceiros e todos...
- Termos Semelhantes
Dois ou mais termos são semelhantes quando têm a mesma parte literal.Exemplos:a) 5m e -7 m são termos semelhantesb) 2xy³ e 9y³x São termos semelhantesObs: veja que não...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...