Matemática

Ilustrações geométricas para alguns fatos algébricos [Parte 1]

Iniciaremos uma série de postagens que pretende ilustrar geometricamente alguns fatos algébricos. Comecemos com a propriedade distributiva:

Em álgebra, uma das técnicas de fatoração bem conhecida consiste em colocar um fator comum em evidência:

ab + ac + ad = a(b + c + d)

Na expressão acima temos uma soma de três parcelas. Cada parcela é um produto. Os três produtos tem o a como um de seus fatores, por isso se diz que ele é um "fator comum".

Este procedimento é uma consequência da "distributividade da multiplicação com relação a soma". Em se tratando das operações de multiplicação e de adição, a propriedade distributiva diz que se a, b e c são números reais quaisquer, então:

a(b + c) = ab + ac

Esta propriedade (que pode ser estendida para mais de duas parcelas dentro dos parenteses - e que sendo lida da esquerda para a direita constitui justamente o caso da fatoração por evidência) geralmente é ensinada, no fundamental, por meio de alguns pequenos arcos:

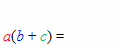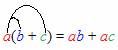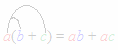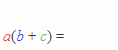Em estudos posteriores é comum vermos a propriedade distributiva (as vezes chamada "lei" distributiva) ser apresentada como um axioma (ou seja, como uma proposição que não precisa ter sua validade demonstrada para ser aceita). Contudo, vamos restringir nosso estudo ao conjunto {1, 2, 3, ..., n, ...} dos números naturais e ver como ela pode ser geometricamente demonstrada. O argumento é de tal modo simples que mesmo crianças podem compreendê-lo.

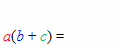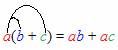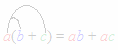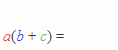
Considere então que a, b, c e d são números naturais. Vejamos em uma interpretação geométrica que, de fato, vale a seguinte igualdade:

ab + ac + ad = a(b + c + d)

Inicialmente lembre-se que a área de um retângulo é o produto da base pela altura. Agora:

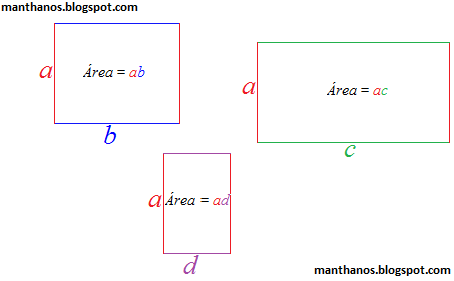
Interprete o termo ab como sendo a área de um retângulo de altura a e base b;

Interprete o termo ac como sendo a área de um retângulo de altura a e base c;

Interprete o termo ad como sendo a área de um retângulo de altura a e base d, conforme as figuras abaixo:

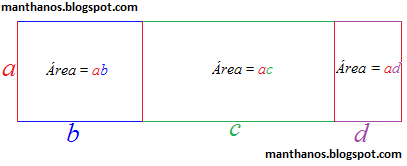
Note que justapondo os três retângulos acima podemos obter um novo retângulo de altura a e base (b + c + d):

Agora, tudo o que temos que fazer é responder a seguinte questão: Qual é a área do retângulo grande acima - que é formado pelos três retângulos menores? (vamos chamar esta área de Ar).

Há pelo menos duas maneiras de responder a esta pergunta:

A primeira delas é notando que Ar (a área do retângulo maior) é a soma das áreas dos três retângulos menores que o forma, ou seja:

Ar = ab + ac + ad

A segunda maneira é fazendo uso do que já dissemos (que a área de um retângulo é o produto da base pela altura):

Ar = a(b + c + d)

A conclusão é imediata:

ab + ac + ad = a(b + c + d)

Ou se preferir:

a(b + c + d) = ab + ac + ad

Assim ficam geometricamente demonstradas tanto a propriedade distributiva quanto a técnica de fatoração por evidência (que são cosias equivalentes) para os casos em que a, b, c e d são todos números positivos.

Observações:___________________________________________________

As figuras acima supõe, evidentemente, que d < a < b < c. Mas o raciocínio é válido independentemente da relação entre as medidas a, b, c e d.

O termo que é colocado em evidência (neste caso o a) foi interpretado como sendo a altura de cada retângulo, mas nada impede que ele seja interpretado como sendo a base de cada um deles (daí a altura seria (b + c + d)).

Pode-se fazer esta demonstração com papel e tesoura - o que pode ser bastante atrativo para as crianças. Basta construir, por exemplo, três retângulos de mesma altura e então, com eles (como se fossem peças de um quebra-cabeça) montar um quarto retângulo, fazendo as observações necessárias.

Por volta de dois mil anos atrás Euclides de Alexandria apresentou na primeira proposição do Livro II da obra Os Elementos sua versão do enunciado e da demonstração da propriedade tratada acima. Na verdade, para significar que ab + ac + ad = a(b + c + d) o que ele disse (numa linguagem totalmente geométrica e, talvez, pouco compreensível) foi o seguinte:

Caso existam duas retas, e uma delas seja cortada em segmentos, quantos quer que sejam, o retângulo contido pelas duas retas é igual aos retângulos contidos tanto pela não cortada quanto por cada um dos segmentos.

A demonstração dele consiste em construir uma figura parecida com o último retângulo mostrado acima e concluir que o retângulo maior é igual à soma dos retângulos menores (pois eles coincidem). Para isso ele usa algumas proposições já demonstradas no Livro I (a saber, as proposições 3, 11, 31 e 34).

_______________________________________________________________

[veja parte 2]

Referência: Livros de álgebra; Os Elementos de Euclides.

Erros podem ser relatados aqui.

- Questão 38 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Deseja-se construir uma calçada contornando dois lados consecutivos de um jardim, cuja forma é retangular, conforme mostra a figura: Sabe-se que o terreno de 12 m por 8 m é também retangular. Assim, se a área da calçada em torno do jardim for igual...

- Questão 50 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Uma caixa no formato de um paralelepípedo reto retângulo, com dimensões 3, 2 e 5 centímetros, possui o mesmo volume de uma caixa no formato de uma pirâmide de base quadrada e 5 centímetros de altura. A área da base dessa pirâmide, em cm2, é (A)...

- Post De Número 260
É com muita felicidade, que nós do Clave de Pi chgamos a marca de nosso post de numero 260. Agradecemos a todos que acessam nosso blog, pois sem vocês nada existiria. Também agradecemos a todos que comentam em nosso blog, aos nossos parceiros e todos...

- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...

- Área Do Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...

Matemática