A Lei da Gravitação Universal e o Campo Gravitacional
A Gravitação Universal
Johanes Kepler (1571-1630) foi um grande conhecedor de Matemática e dedicou parte de sua vida à análise sobre as posições dos planetas.
Através de cálculos matemáticos, Kepler fez diversas tentativas para comprovar as órbitas planetárias circulares descritas pelo seu mestre Tycho Brahe, conseguindo somente aproximações. Por fim, chegou às órbitas elípticas e às leis que fizeram avançar a Astronomia.
1ª Lei - Lei das Órbitas: Cada Planeta descreve uma órbita elíptica em torno do Sol, onde este é um dos focos da elipse:
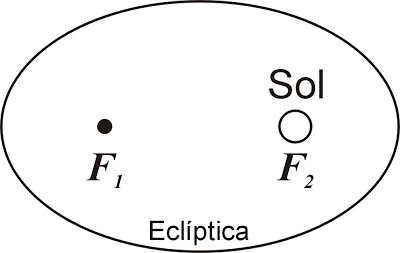 2ª Lei - Lei das Áreas: A reta que liga o Sol ao Planeta, descreve áreas iguais para intervalos de tempo iguais:
2ª Lei - Lei das Áreas: A reta que liga o Sol ao Planeta, descreve áreas iguais para intervalos de tempo iguais:
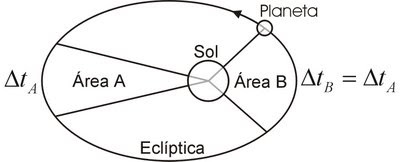
3ª Lei - Lei dos Períodos: O quadrado do período do movimento do Planeta ao redor do Sol, dividido pela distância média do Planeta ao Sol elevado ao cubo é uma constante para todos os Planetas:


onde:
T é o período de revolução do Planeta ao redor do Sol;
K é a constante de proporcionalidade;
R é a distância média do Planeta ao Sol.
Apesar das Leis de Kepler permitirem grandes avanços na Astronomia, havia uma pergunta sem resposta: "Que espécie de força o Sol exerce sobre os Planetas obrigando-os a movimentarem-se de acordo com as Leis descobertas por Kepler?"
Newton respondeu essa questão, orientando-se pelas próprias Leia de Kepler e aplicando ao movimento da Lua as três Leis que Newton mesmo descobrira, chegou à Lei da Gravitação Universal, cujo enunciado pode ser expresso da seguinte forma:
"Matéria atrai matéria com uma força diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância entre elas."
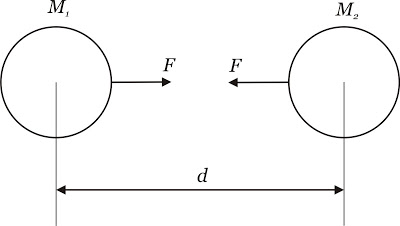
![clip_image002[6] clip_image002[6]](matematica/matematica-57ac275402448.gif?imgmax=800)
onde:
F é a força em Newtons (N)
M é a massa em quilogramas (kg)
d é a distância em metros (m)
G é a constante gravitacional em Newtons metro quadrado por quilograma quadrado (Nm2 / kg2).
Para transformar uma proporcionalidade em uma igualdade, temos que inserir uma constante de proporcionalidade, que, no caso da gravitação, é a constante G, também chamada de Constante de Gravitação Universal.
A constante G tem um valor muito pequeno e não foi descoberto seu valor por Newton, somente algum tempo depois Cavendish, através de um experimento em laboratório, encontrou numericamente seu valor:
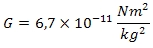
Sua unidade de medida é dada por:
![clip_image002[10] clip_image002[10]](matematica/matematica-57ac275404f49.gif?imgmax=800)
![clip_image004[4] clip_image004[4]](matematica/matematica-57ac275406537.gif?imgmax=800)

Exemplo 1: Duas pessoas de massas respectivamente iguais a 80kg e 60kg estão 6m distantes uma da outra. Determinar a força de atração gravitacional entre elas.
Sabemos que:
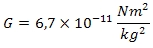
![clip_image002[12] clip_image002[12]](matematica/matematica-57ac27540a17f.gif?imgmax=800)
![clip_image004[6] clip_image004[6]](matematica/matematica-57ac27540b4bf.gif?imgmax=800)
![clip_image006[4] clip_image006[4]](matematica/matematica-57ac27540c71c.gif?imgmax=800)
Pela fórmula da Gravitação Universal temos:
![clip_image002[10] clip_image002[10]](matematica/matematica-57ac275404f49.gif?imgmax=800)
![clip_image002[14] clip_image002[14]](matematica/matematica-57ac27540ed02.gif?imgmax=800)
![clip_image004[8] clip_image004[8]](matematica/matematica-57ac27540ff9c.gif?imgmax=800)
Como podemos notar, a força de atração entre duas pessoas é muito pequena.
Exemplo 2: Calcular a força de atração entre a Terra e a Lua, considerando:

![clip_image004[12] clip_image004[12]](matematica/matematica-57ac2754123f9.gif?imgmax=800)
![clip_image006[8] clip_image006[8]](matematica/matematica-57ac275413573.gif?imgmax=800)
![clip_image002[10] clip_image002[10]](matematica/matematica-57ac275404f49.gif?imgmax=800)
![clip_image002[20] clip_image002[20]](matematica/matematica-57ac2754157ee.gif?imgmax=800)
![clip_image004[14] clip_image004[14]](matematica/matematica-57ac2754168b3.gif?imgmax=800)
![clip_image006[10] clip_image006[10]](matematica/matematica-57ac275417a38.gif?imgmax=800)
Como podemos notar, a Lei da Gravitação de Newton só tem sentido com corpos de massa muito grande, encontrando uma força de atração de F = 2,03 X 1020 N, diferentemente da força encontrada no exemplo 1, que é desprezível.
Exemplo 3: Calcular a força de atração entre o Sol e a Terra, considerando:
![clip_image002[22] clip_image002[22]](matematica/matematica-57ac275418a76.gif?imgmax=800)
![clip_image004[16] clip_image004[16]](matematica/matematica-57ac275419b07.gif?imgmax=800)
![clip_image006[12] clip_image006[12]](matematica/matematica-57ac27541ab21.gif?imgmax=800)
![clip_image002[10] clip_image002[10]](matematica/matematica-57ac275404f49.gif?imgmax=800)
![clip_image002[24] clip_image002[24]](matematica/matematica-57ac27541cb25.gif?imgmax=800)
![clip_image004[18] clip_image004[18]](matematica/matematica-57ac27541da7c.gif?imgmax=800)
![clip_image006[14] clip_image006[14]](matematica/matematica-57ac27541eaca.gif?imgmax=800)
O Campo Gravitacional
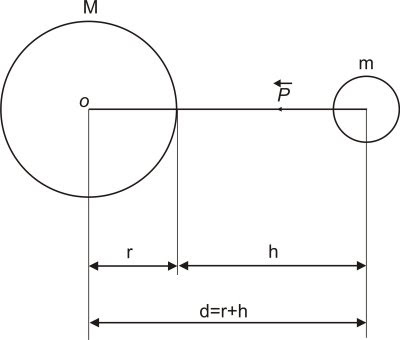
A intensidade do campo gravitacional em um ponto, a uma certa distância d do centro da Terra, pode ser calculada através de algumas relações:
 Pela segunda Lei de Newton, temos que:
Pela segunda Lei de Newton, temos que:
![clip_image002[26] clip_image002[26]](matematica/matematica-57ac2754209b0.gif?imgmax=800)
Pela Lei da Gravitação Universal, temos que:
![clip_image002[28] clip_image002[28]](matematica/matematica-57ac2754218ab.gif?imgmax=800)
Substituindo (1) em (2), temos:
![clip_image002[30] clip_image002[30]](matematica/matematica-57ac2754227d0.gif?imgmax=800)
![clip_image002[32] clip_image002[32]](matematica/matematica-57ac275423651.gif?imgmax=800)
![clip_image004[20] clip_image004[20]](matematica/matematica-57ac27542450a.gif?imgmax=800)
A aceleração da gravidade em um ponto é a Força G multiplicada pela massa do Planeta dividido pelo quadrado da distância.
Mas, d = r + h, então:
![clip_image002[34] clip_image002[34]](matematica/matematica-57ac275425333.gif?imgmax=800)
Vejam que g depende de uma altura h e do raio r do planeta. Se a altura h tende a zero, a distância será o próprio raio r do Planeta:
![clip_image002[36] clip_image002[36]](matematica/matematica-57ac2754261ac.gif?imgmax=800)
onde g0 é a aceleração da gravidade na superfície do Planeta.
Ainda assim dependemos da massa M do Planeta e da constante G. Se dividirmos (3) por (4), teremos:
![clip_image002[38] clip_image002[38]](matematica/matematica-57ac275426fa8.gif?imgmax=800)
![clip_image004[22] clip_image004[22]](matematica/matematica-57ac275427d70.gif?imgmax=800)
![clip_image006[16] clip_image006[16]](matematica/matematica-57ac275428b35.gif?imgmax=800)

Com esta equação não dependemos da massa do Planeta, somente da aceleração na superfície.
Exemplo 4: A aceleração da superfície da Lua é de aproximadamente gL = 2m / s2, na superfície da Terra é aproximadamente gT = 10m / s2. Sabendo que a razão entre os raios da Lua e da Terra 1/4, calcular as massas da Lua e da Terra.
![clip_image002[42] clip_image002[42]](matematica/matematica-57ac27542a67d.gif?imgmax=800)
![clip_image004[26] clip_image004[26]](matematica/matematica-57ac27542b3cc.gif?imgmax=800)
![clip_image006[20] clip_image006[20]](matematica/matematica-57ac27542c110.gif?imgmax=800)
![clip_image008[6] clip_image008[6]](matematica/matematica-57ac27542ce3f.gif?imgmax=800)
![clip_image010[4] clip_image010[4]](matematica/matematica-57ac27542dbd0.gif?imgmax=800)
![clip_image012[4] clip_image012[4]](matematica/matematica-57ac27542e930.gif?imgmax=800)
![clip_image014[4] clip_image014[4]](matematica/matematica-57ac27542f632.gif?imgmax=800)
![clip_image016[4] clip_image016[4]](matematica/matematica-57ac27543033b.gif?imgmax=800)
![clip_image018[4] clip_image018[4]](matematica/matematica-57ac275430ffe.gif?imgmax=800)
![clip_image020[4] clip_image020[4]](matematica/matematica-57ac275431d1c.gif?imgmax=800)
![clip_image022[4] clip_image022[4]](matematica/matematica-57ac2754329d7.gif?imgmax=800)
![clip_image024[4] clip_image024[4]](matematica/matematica-57ac27543363a.gif?imgmax=800)
![clip_image026[4] clip_image026[4]](matematica/matematica-57ac275434311.gif?imgmax=800)
Concluímos que a Terra é cerca de 80 vezes a massa da Lua.
Veja mais: A Gravitação Universal Além do Sistema Solar
As Quatro Forças Básicas da Natureza
As Velocidades da Terra
- O Sistema Solar
O Sistema Solar O sistema solar é um conjunto de planetas, asteróides e cometas que giram ao redor do sol. Cada um se mantém em sua respectiva órbita em virtude da intensa força gravitacional exercida pelo astro, que possui massa muito maior que...
- Determinando A Massa Da Terra
Uma das consequências das Leis de Newton, Galileu e Kepler é a determinação da Massa da Terra. Vamos estimar sua massa usando para isso apenas equações simples, tão conhecidas de alunos do ensino médio. Newton publicou em sua obra Philosophiae...
- As Velocidades Da Terra
Sabemos que a Terra executa alguns movimentos no decorrer de sua órbita ao redor do Sol. Vamos destacar os principais: Rotação e Translação. Vamos determinar as velocidades em que a Terra desenvolve em cada um desses movimentos. Movimento de RotaçãoA...
- Aceleração
A aceleração é a taxa de variação da velocidade em relação ao tempo. Analogamente à velocidade instantânea, temos: Ou seja, a aceleração instantânea é a derivada em relação ao tempo da velocidade instantânea: que é a derivada segunda...
- Cálculo Do Centro De Massa Do Binário Terra-lua
Para calcular o baricentro, ou centro de massa, do binário Terra-Lua, primeiramente vamos considerar: (RT) sendo o raio médio da Terra = 6.378km (RL) sendo o raio da Lua = 1.738km (MT) sendo a massa da Terra = 5,98 x 1024kg (ML) sendo a massa...
