Matemática

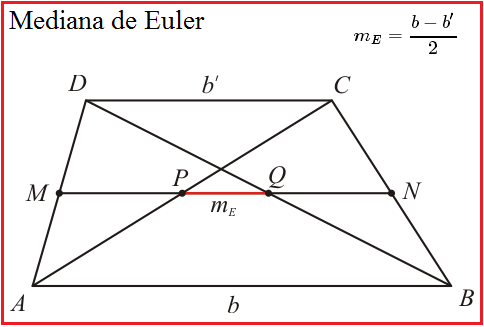
A Mediana de Euler

Leonhard Euler $(1707-1783)$ foi um dos maiores matemáticos (ou o maior) do século $XVIII$, pois sua obra é impressionante, pela quantidade e pela diversidade. Dentre algumas áreas em que Euler contribuiu, podemos citar a Álgebra, Teoria dos Números, Trigonometria, Cálculo Infinitesimal, Óptica e Geometria. Desta última, especificamente em Geometria Plana, Euler também deixou sua marca num estudo sobre quadriláteros.

Definição $1$: Mediana de Euler é o segmento que une os pontos médios das diagonais de um trapézio e fica localizada sobre sua base média, expressa por:

\begin{equation}
m_E=\frac{b-b'}{2}
\end{equation}

onde $m_E$ é a Mediana de Euler e $b$ e $b'$ são as bases maior e menor, respectivamente, do trapézio.

Ao traçarmos as duas diagonais do trapézio, estas cortam a base média nos pontos $P$ e $Q$. A Mediana de Euler é o segmento $\overline{PQ}$.

A demonstração não é muito complicada, pois remete a temas já estudados, como a base média de um triângulo e a base média de um trapézio.

Do triângulo $ABD$, temos que sua base média é o segmento $\overline{MQ}$, dada por:

\begin{equation}
\overline{MQ}=\frac{\overline{AB}}{2}=\frac{b}{2}
\end{equation}

E do triângulo $ACD$, temos que sua base média é o segmento $\overline{MP}$, dada por:

\begin{equation}
\overline{MP}=\frac{\overline{CD}}{2}=\frac{b'}{2}
\end{equation}

A Mediana de Euler é o segmento $\overline{PQ}$, que pode ser expresso por:

\begin{equation}
\overline{PQ}=\overline{MQ}-\overline{MP}
\end{equation}

Substiruindo $(2)$ e $(3)$ em $(5)$, obtemos:

\begin{equation}
\overline{PQ}=m_E=\frac{b}{2}-\frac{b'}{2}=\frac{b-b'}{2}
\end{equation}

Exemplo $1$: Seja o trapézio $ABCD$ de bases $b=\overline{AB}=12cm$ e $b'=\overline{CD}=8cm$. Calcular a Mediana de Euler.

Aplicando a fórmula dada em $(5)$, temos que:

$$m_E=\frac{b-b'}{2}=\frac{12-8}{2}=2cm$$

Veja mais:

Base Média de um Trapézio
Base Média de um Triângulo
Demonstração da Identidade de Euler

- Baricentro
As três medianas de um triângulo interceptam-se num mesmo ponto que divide cada mediana em duas partes tais que a parte que contém o vértice é o dobro da outra. Se $$\overline{AM_1}\text{,}\overline{BM_2}\text{,}\overline{CM_3}$$ são as medianas...

- Razão De Secção
Consideremos três pontos: $A(x_a,y_a)$, $B(x_b,y_b)$ e $C(x_c,y_c)$, pertencentes a uma mesma reta $r$, oblíqua aos eixos $x$ e $y$ e ainda sendo $B$ e $C$ distintos. Definição:A razão $k$ das medidas algébricas de $\overline{AC}$ e $\overline{CB}$...

- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...

- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...

- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...

Matemática