Matemática
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras.
Considere o círculo trigonométrico abaixo de raio unitário:
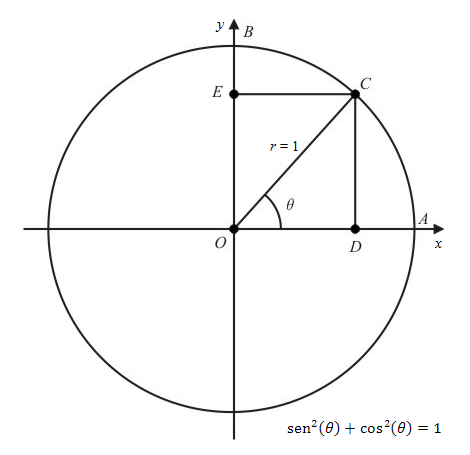
O ponto $C$ é um ponto genérico sobre a circunferência e o segmento $\overline{OC}$ forma um ângulo $\theta$ com o eixo dos $x$.
O segmento $\overline{OD}$ é a projeção do segmento $\overline{OC}$ sobre eixo dos $x$ que é o cosseno do ângulo $\theta$; e o segmento $\overline{OE}$ é a projeção do segmento $\overline{OC}$ sobre o eixo dos $y$ que é o seno do ângulo $\theta$.
Assim, podemos destacar as seguintes relações:
\begin{equation}
\overline{OD}^2 + \overline{DC}^2 = \overline{OC}^2
\end{equation}
\begin{equation}
\overline{OD} = \cos(\theta)
\end{equation}
\begin{equation}
\overline{DC} = \text{sen}(\theta)
\end{equation}
\begin{equation}
\overline{OC} = 1 \quad \text{(raio de tamanho unitário)}
\end{equation}
Substituindo $(2)$, $(3)$ e $(4)$ na relação $(1)$, obtemos:
\begin{equation}
\text{sen}^2 (\theta) + \cos^2(\theta) = 1
\end{equation}
Esta relação é válida para qualquer ângulo $\theta$.
Usamos a relação fundamental:
\begin{equation*}
\text{sen}^2 (\theta) + \cos^2(\theta) = 1\\
\left(\frac{1}{2}\right)^2 + \cos^2(\theta) = 1\\
\cos^2(\theta) = 1 - \frac{1}{4}\\
\cos^2(\theta) = \frac{3}{4}\\
\cos(\theta) = \frac{\sqrt{3}}{2}
\end{equation*}
O ângulo cujo seno vale $1/2$ e o cosseno vale $\sqrt{3}/2$ é o ângulo $\theta = 30°$.
Tabela Trigonométrica dos Ângulos do Primeiro Quadrante
Demonstração de Funções Trigonométricas do Semi-Arco
Demonstração de Funções Trigonométricas do Arco-Duplo

- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
Matemática
Demonstração da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras.
Considere o círculo trigonométrico abaixo de raio unitário:

O ponto $C$ é um ponto genérico sobre a circunferência e o segmento $\overline{OC}$ forma um ângulo $\theta$ com o eixo dos $x$.
O segmento $\overline{OD}$ é a projeção do segmento $\overline{OC}$ sobre eixo dos $x$ que é o cosseno do ângulo $\theta$; e o segmento $\overline{OE}$ é a projeção do segmento $\overline{OC}$ sobre o eixo dos $y$ que é o seno do ângulo $\theta$.
Assim, podemos destacar as seguintes relações:
\begin{equation}
\overline{OD}^2 + \overline{DC}^2 = \overline{OC}^2
\end{equation}
\begin{equation}
\overline{OD} = \cos(\theta)
\end{equation}
\begin{equation}
\overline{DC} = \text{sen}(\theta)
\end{equation}
\begin{equation}
\overline{OC} = 1 \quad \text{(raio de tamanho unitário)}
\end{equation}
Substituindo $(2)$, $(3)$ e $(4)$ na relação $(1)$, obtemos:
\begin{equation}
\text{sen}^2 (\theta) + \cos^2(\theta) = 1
\end{equation}
Esta relação é válida para qualquer ângulo $\theta$.
Exemplo:
Dado $\displaystyle \text{sen}(\theta) = \frac{1}{2}$, determinar $\cos (\theta)$.Usamos a relação fundamental:
\begin{equation*}
\text{sen}^2 (\theta) + \cos^2(\theta) = 1\\
\left(\frac{1}{2}\right)^2 + \cos^2(\theta) = 1\\
\cos^2(\theta) = 1 - \frac{1}{4}\\
\cos^2(\theta) = \frac{3}{4}\\
\cos(\theta) = \frac{\sqrt{3}}{2}
\end{equation*}
O ângulo cujo seno vale $1/2$ e o cosseno vale $\sqrt{3}/2$ é o ângulo $\theta = 30°$.
Veja mais:
Demonstração dos Ângulos NotáveisTabela Trigonométrica dos Ângulos do Primeiro Quadrante
Demonstração de Funções Trigonométricas do Semi-Arco
Demonstração de Funções Trigonométricas do Arco-Duplo

- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
