Matemática
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade.
\begin{equation}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\end{equation}
de modo que satisfaz a relação:
\begin{equation}
a^2=b^2+c^2
\end{equation}
Sua excentricidade é definida por:
\begin{equation}
e=\frac{c}{a}
\end{equation}
Para determinarmos o comprimento desta elipse, usaremos a fórmula para o cálculo de um segmento de curva, cuja dedução pode ser vista neste link:
\begin{equation}
L = \int dl = \int_a^b \sqrt{1+(y^\prime)^2}\ dx
\end{equation}
Derivando implicitamente a relação $(1)$, em relação a $x$, obtemos:
\begin{equation*}
\frac{2x}{a^2} + \frac{2y}{b^2}\ y^{\prime} = 0\\
y^{\prime} = -\frac{b^2x}{a^2y}
\end{equation*}
Elevando ambos os lados ao quadrado e depois somando $1$ em cada lado, obtemos:
\begin{equation}
1+(y^{\prime})^2 = 1+\frac{b^4x^2}{a^4y^2}
\end{equation}
Isolando $y^2$ da relação $(1)$, obtemos:
\begin{equation}
y^2 = b^2\left(1-\frac{x^2}{a^2}\right)
\end{equation}
Substituindo a relação $(6)$ na $(5)$ e simplificando, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{a^4 - (a^2-b^2)x^2}{a^2(a^2-x^2)}
\end{equation}
Substituindo a relação $(2)$ na relação $(7)$, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{a^4-c^2x^2}{a^2(a^2-x^2)}
\end{equation}
Dividindo o numerado e o denominador do segundo membro da relação acima, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{\displaystyle a^2 - \frac{c^2x^2}{a^2}}{a^2-x^2}
\end{equation}
Substituindo a relação $(3)$, na relação acima, obtemos:
\begin{equation}
1 + (y^{\prime})^2 = \frac{a^2 - e^2x^2}{a^2-x^2}
\end{equation}
Substituindo a relação $(9)$ em $(4)$, obtemos:
\begin{equation}
L= 4 \int_0^a \sqrt{\frac{a^2 - e^2x^2}{a^2-x^2}} dx
\end{equation}
Fazendo uma substituição trigonométrica onde $x=a\ \text{sen}(\theta)$, temos que $dx=a\ \cos (\theta)\ d\theta$. Para $x=0$, temos $\theta=0$ e para $x=a$, temos $\displaystyle \theta = \frac{\pi}{2}$. Assim:
\begin{equation*}
L = 4\int_0^{\pi/2} \sqrt{\frac{a^2-e^2a^2\text{sen}^2(\theta)}{a^2-a^2\text{sen}^2(\theta)}}\cdot a\ \cos(\theta) d\theta\\
\ \\
L = 4 \int_0^{\pi/2} \sqrt{\frac{1-e^2 \text{sen}^2(\theta)}{\cos^2(\theta)}}\cdot a\ \cos(\theta) d\theta
\end{equation*}
\begin{equation}
L = 4a\int_0^{\pi/2} \sqrt{1-e^2 \text{sen}^2(\theta)}\ d\theta
\end{equation}
Observe que se $e=0$, a elipse representa uma circunferência de raio a e segue da expressão $(12)$ que $L=2\pi a$ como era esperado.
A integral dada em $(12)$ é uma integral elíptica e já foi amplamente estudada por grandes matemáticos que mostraram não ser possível que expressar a integral acima em termos de funções elementares. Deste modo, para obter uma fórmula para comprimento da elipse, iremos expandir o integrando através do binômio de Newton, ou seja:
\begin{equation*}
(1+x)^n = 1+nx+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+\cdots
\end{equation*}
Fazendo $\displaystyle n=\frac{1}{2}$ e $x=-e^2\text{sen}^2(\theta)$, obtemos:
\begin{equation*}
\left( 1-e^2\text{sen}^2(\theta) \right)^{1/2}\simeq 1 - \frac{e^2\text{sen}^2(\theta)}{2} - \frac{e^4\text{sen}^4(\theta)}{8} - \frac{e^6\text{sen}^6(\theta)}{16}
\end{equation*}
Substituindo a relação a cima em $(12)$ e integrando termo a termo, obtemos a fórmula aproximada para calcular o comprimento de uma elipse em função de sua excentricidade e do seu eixo maior, isto é:
\begin{equation}
L \simeq \pi a \left(2-\frac{e^2}{2} - \frac{3e^4}{32} - \frac{5e^6}{128} \right)
\end{equation}
Resolução: Note que o semieixo maior é $a=25m$ e o semieixo menor é $b=20m$, de modo que $\displaystyle c=\sqrt{25^2-20^2}=15m$ e a excentricidade é $\displaystyle e=\frac{c}{a}=\frac{15}{25}=0,6$. Usando a fórmula dada em $(13)$ segue que o comprimento de arame para dar uma volta é:
\begin{equation*}
L \simeq \pi \cdot 25 \left(2-\frac{0,6^2}{2} - \frac{3\cdot 0,6^4}{32}-\frac{5\cdot 0,6^6}{128} \right) = 141,8451m
\end{equation*}
Portanto, o comprimento mínimo necessário de arame para cercar o canteiro elíptico é:
\begin{equation*}
141,851 \times 3 \simeq 425,5m
\end{equation*}
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Triângulos de áreas constantes na elipse
A equação da elipse

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Uma fórmula para calcular o comprimento da elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade.

Dedução
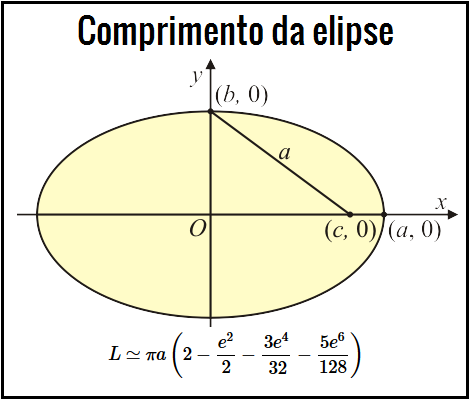
Seja a elipse de semieixo maior $a$ e semieixo menor $b$, centrada na origem, conforme a figura acima. Sejam os pontos $(\pm c ,0)$ os focos elipse de equação reduzida dada por:\begin{equation}
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\end{equation}
de modo que satisfaz a relação:
\begin{equation}
a^2=b^2+c^2
\end{equation}
Sua excentricidade é definida por:
\begin{equation}
e=\frac{c}{a}
\end{equation}
Para determinarmos o comprimento desta elipse, usaremos a fórmula para o cálculo de um segmento de curva, cuja dedução pode ser vista neste link:
\begin{equation}
L = \int dl = \int_a^b \sqrt{1+(y^\prime)^2}\ dx
\end{equation}
Derivando implicitamente a relação $(1)$, em relação a $x$, obtemos:
\begin{equation*}
\frac{2x}{a^2} + \frac{2y}{b^2}\ y^{\prime} = 0\\
y^{\prime} = -\frac{b^2x}{a^2y}
\end{equation*}
Elevando ambos os lados ao quadrado e depois somando $1$ em cada lado, obtemos:
\begin{equation}
1+(y^{\prime})^2 = 1+\frac{b^4x^2}{a^4y^2}
\end{equation}
Isolando $y^2$ da relação $(1)$, obtemos:
\begin{equation}
y^2 = b^2\left(1-\frac{x^2}{a^2}\right)
\end{equation}
Substituindo a relação $(6)$ na $(5)$ e simplificando, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{a^4 - (a^2-b^2)x^2}{a^2(a^2-x^2)}
\end{equation}
Substituindo a relação $(2)$ na relação $(7)$, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{a^4-c^2x^2}{a^2(a^2-x^2)}
\end{equation}
Dividindo o numerado e o denominador do segundo membro da relação acima, obtemos:
\begin{equation}
1+(y^{\prime})^2 = \frac{\displaystyle a^2 - \frac{c^2x^2}{a^2}}{a^2-x^2}
\end{equation}
Substituindo a relação $(3)$, na relação acima, obtemos:
\begin{equation}
1 + (y^{\prime})^2 = \frac{a^2 - e^2x^2}{a^2-x^2}
\end{equation}
Substituindo a relação $(9)$ em $(4)$, obtemos:
\begin{equation}
L= 4 \int_0^a \sqrt{\frac{a^2 - e^2x^2}{a^2-x^2}} dx
\end{equation}
Fazendo uma substituição trigonométrica onde $x=a\ \text{sen}(\theta)$, temos que $dx=a\ \cos (\theta)\ d\theta$. Para $x=0$, temos $\theta=0$ e para $x=a$, temos $\displaystyle \theta = \frac{\pi}{2}$. Assim:
\begin{equation*}
L = 4\int_0^{\pi/2} \sqrt{\frac{a^2-e^2a^2\text{sen}^2(\theta)}{a^2-a^2\text{sen}^2(\theta)}}\cdot a\ \cos(\theta) d\theta\\
\ \\
L = 4 \int_0^{\pi/2} \sqrt{\frac{1-e^2 \text{sen}^2(\theta)}{\cos^2(\theta)}}\cdot a\ \cos(\theta) d\theta
\end{equation*}
\begin{equation}
L = 4a\int_0^{\pi/2} \sqrt{1-e^2 \text{sen}^2(\theta)}\ d\theta
\end{equation}
Observe que se $e=0$, a elipse representa uma circunferência de raio a e segue da expressão $(12)$ que $L=2\pi a$ como era esperado.
A integral dada em $(12)$ é uma integral elíptica e já foi amplamente estudada por grandes matemáticos que mostraram não ser possível que expressar a integral acima em termos de funções elementares. Deste modo, para obter uma fórmula para comprimento da elipse, iremos expandir o integrando através do binômio de Newton, ou seja:
\begin{equation*}
(1+x)^n = 1+nx+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+\cdots
\end{equation*}
Fazendo $\displaystyle n=\frac{1}{2}$ e $x=-e^2\text{sen}^2(\theta)$, obtemos:
\begin{equation*}
\left( 1-e^2\text{sen}^2(\theta) \right)^{1/2}\simeq 1 - \frac{e^2\text{sen}^2(\theta)}{2} - \frac{e^4\text{sen}^4(\theta)}{8} - \frac{e^6\text{sen}^6(\theta)}{16}
\end{equation*}
Substituindo a relação a cima em $(12)$ e integrando termo a termo, obtemos a fórmula aproximada para calcular o comprimento de uma elipse em função de sua excentricidade e do seu eixo maior, isto é:
\begin{equation}
L \simeq \pi a \left(2-\frac{e^2}{2} - \frac{3e^4}{32} - \frac{5e^6}{128} \right)
\end{equation}
Exemplo
Um jardineiro é contratado para construir um canteiro no formato de uma elipse de eixos iguais $40 m$ e $50 m$ respectivamente. Para delimitá-lo, o jardineiro construirá uma cerca com estacas e $3$ voltas de arame. Determine a quantidade de arame necessário para este projeto.Resolução: Note que o semieixo maior é $a=25m$ e o semieixo menor é $b=20m$, de modo que $\displaystyle c=\sqrt{25^2-20^2}=15m$ e a excentricidade é $\displaystyle e=\frac{c}{a}=\frac{15}{25}=0,6$. Usando a fórmula dada em $(13)$ segue que o comprimento de arame para dar uma volta é:
\begin{equation*}
L \simeq \pi \cdot 25 \left(2-\frac{0,6^2}{2} - \frac{3\cdot 0,6^4}{32}-\frac{5\cdot 0,6^6}{128} \right) = 141,8451m
\end{equation*}
Portanto, o comprimento mínimo necessário de arame para cercar o canteiro elíptico é:
\begin{equation*}
141,851 \times 3 \simeq 425,5m
\end{equation*}
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Referências:
[1] Uma fórmula para calcular o comprimento da elipse no blog Fatos MatemáticosVeja mais:
Fórmula para calcular um segmento de curvaTriângulos de áreas constantes na elipse
A equação da elipse

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
