Matemática
m_1\cdot m_2=-1
\end{equation}
\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}\left(\theta+\frac{\pi}{2}\right)}{\cos{\left(\theta+\frac{\pi}{2}\right)}}
\end{equation}
Pela fórmula da soma de arcos, segue que:
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}(\theta)\cos \left ( \frac{\pi}{2} \right )+\text{sen}\left ( \frac{\pi}{2} \right )\cos(\theta)}{\cos(\theta)\cos\left ( \frac{\pi}{2} \right )-\text{sen}(\theta)\text{sen}\left ( \frac{\pi}{2} \right )}$$
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}(\theta)\cdot 0+1\cdot \cos(\theta)}{\cos(\theta)\cdot 0-\text{sen}(\theta)\cdot 1}$$
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=- \frac{\cos(\theta)}{\text{sen}(\theta)}$$
\begin{equation}
\text{tg}\left(\theta+\frac{\pi}{2}\right)=-\text{cotg}(\theta)=-\frac{1}{\text{tg}(\theta)}
\end{equation}
Como $m_1=\text{tg}(\theta)$ e $\displaystyle m_2=\text{tg}\left(\theta+\frac{\pi}{2}\right)=-\frac{1}{\text{tg}(\theta)}$, podemos dizer que:
\begin{equation}
\begin{matrix}
m_2=-\frac{1}{m_1}\\
\text{ou}\\
m_1\cdot m_2=-1\\
\end{matrix}
\end{equation}
Exemplos: Verifique se as retas são perpendiculares.
a) $r_1:x+2y-1=0$ e $r_2:2x-y+3=0$
O coeficiente angular de uma reta é dada por:
\begin{equation}
y-y_0=m(x-x_0)
\end{equation}
Utilizando a fórmula dada em $(4)$, temos:
$$m_2=-\frac{1}{m_1}$$
De fato, temos:
$$2=-\frac{1}{-1/2} \Rightarrow -1=-1$$
O que mostra que as retas são perpendiculares. Graficamente:
 b) $r_1:x+3y-1=0$ e $r_2:-x-y+4=0$.
b) $r_1:x+3y-1=0$ e $r_2:-x-y+4=0$.
Determinamos os coeficientes angulares das retas:
\begin{matrix}
r_1: y-y_A=m_1(x-x_A)\\
4-3=m_1(-1-0)\\
m_1=-1\\
\end{matrix}
e
\begin{matrix}
r_2: y-y_B=m_2(x-x_B)\\
3-4=m_2(0-1)\\
m_2=1\\
\end{matrix}
Temos que:
\begin{matrix}
m_1 \cdot m_2=-1\\
-1\cdot 1=-1\\
-1=-1\\
\end{matrix}
O que é uma verdade e as retas realmente são perpendiculares. Graficamente:
Veja mais:
Valor Absoluto e a Desigualdade Triangular
Fórmula das Coordenadas de um Triângulo
Reta Tangente a uma Curva

- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.

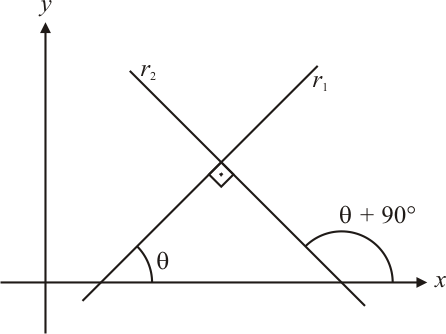
Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das retas $r_1$ e $r_2$, respectivamente. As retas $r_1$ e $r_2$ serão perpendiculares entre si se, e somente se, o ângulo formado entre elas for igual a $90^\circ$.
Teorema $1$: Duas retas são perpendiculares entre si se o coeficiente angular de uma delas for igual ao oposto do inverso da outra, ou seja:
\begin{equation}m_1\cdot m_2=-1
\end{equation}
Demonstração: Sejam $m_1$ o coeficiente angular da reta $r_1$ denotado por $m_1=\text{tg}(\theta)$ e $m_2$ o coeficiente angular da reta $r_2$ denotado por $\displaystyle m_2=\text{tg}\left(\theta + \frac{\pi}{2}\right)$. Temos que:
\begin{equation}\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}\left(\theta+\frac{\pi}{2}\right)}{\cos{\left(\theta+\frac{\pi}{2}\right)}}
\end{equation}
Pela fórmula da soma de arcos, segue que:
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}(\theta)\cos \left ( \frac{\pi}{2} \right )+\text{sen}\left ( \frac{\pi}{2} \right )\cos(\theta)}{\cos(\theta)\cos\left ( \frac{\pi}{2} \right )-\text{sen}(\theta)\text{sen}\left ( \frac{\pi}{2} \right )}$$
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=\frac{\text{sen}(\theta)\cdot 0+1\cdot \cos(\theta)}{\cos(\theta)\cdot 0-\text{sen}(\theta)\cdot 1}$$
$$\text{tg}\left(\theta+\frac{\pi}{2}\right)=- \frac{\cos(\theta)}{\text{sen}(\theta)}$$
\begin{equation}
\text{tg}\left(\theta+\frac{\pi}{2}\right)=-\text{cotg}(\theta)=-\frac{1}{\text{tg}(\theta)}
\end{equation}
Como $m_1=\text{tg}(\theta)$ e $\displaystyle m_2=\text{tg}\left(\theta+\frac{\pi}{2}\right)=-\frac{1}{\text{tg}(\theta)}$, podemos dizer que:
\begin{equation}
\begin{matrix}
m_2=-\frac{1}{m_1}\\
\text{ou}\\
m_1\cdot m_2=-1\\
\end{matrix}
\end{equation}
Exemplos: Verifique se as retas são perpendiculares.
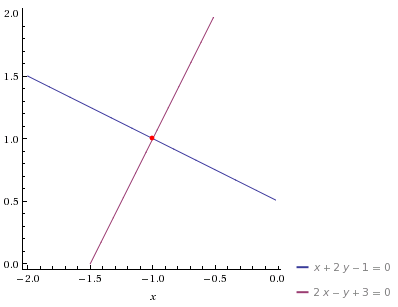
a) $r_1:x+2y-1=0$ e $r_2:2x-y+3=0$
O coeficiente angular de uma reta é dada por:
\begin{equation}
y-y_0=m(x-x_0)
\end{equation}
As equações das retas dadas estão na forma geral: $ax+by+c=0$. Isolando $y$ colocamos-as na forma reduzida: $y=mx+q$, onde $m=-a/b$ e $q=-c/b$, sendo $m$ o coeficiente angular da reta. Assim, temos: $\displaystyle r_1:y=-\frac{1}{2}x+\frac{1}{2}$ e $\displaystyle r_2:y=2x-3$. Assim, $m_1=-1/2$ e $m_2=2$.
Utilizando a fórmula dada em $(4)$, temos:
$$m_2=-\frac{1}{m_1}$$
De fato, temos:
$$2=-\frac{1}{-1/2} \Rightarrow -1=-1$$
O que mostra que as retas são perpendiculares. Graficamente:

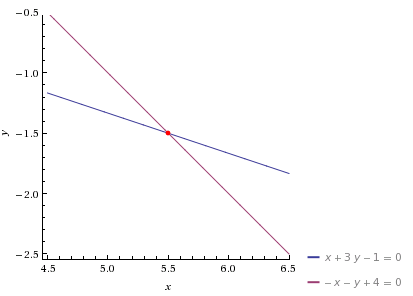
Escrevendo as retas na forma reduzida, temos: $r_1:x+3y-1=0$ e $r_2:-x-y+4=0$ e os respectivos coeficientes angulares são $m_1=-1/3$ e $m_2=-1$. Vemos que as retas não são perpendiculares, já que ambos os coeficientes angulares são negativos, onde o produto será um número positivo. Graficamente:

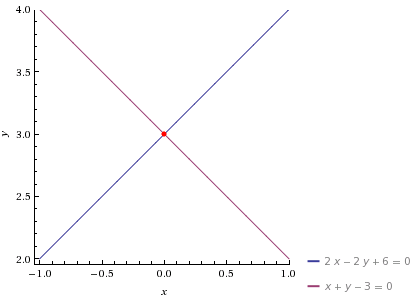
c) Sejam as retas $r_1$ passa pelo ponto $A_1(0,3)$ e $A_2(-1,4)$ e a reta $r_2$ passa pelo ponto $B_1(1,4)$ e $B_2(0,3)$.
Determinamos os coeficientes angulares das retas:
\begin{matrix}
r_1: y-y_A=m_1(x-x_A)\\
4-3=m_1(-1-0)\\
m_1=-1\\
\end{matrix}
e
\begin{matrix}
r_2: y-y_B=m_2(x-x_B)\\
3-4=m_2(0-1)\\
m_2=1\\
\end{matrix}
Temos que:
\begin{matrix}
m_1 \cdot m_2=-1\\
-1\cdot 1=-1\\
-1=-1\\
\end{matrix}
O que é uma verdade e as retas realmente são perpendiculares. Graficamente:

Veja mais:
Valor Absoluto e a Desigualdade Triangular
Fórmula das Coordenadas de um Triângulo
Reta Tangente a uma Curva

- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
