Matemática
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios.
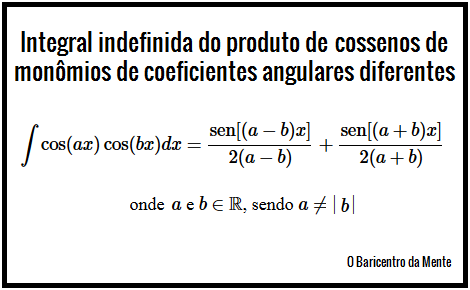
Vamos demonstrar que:
\begin{equation}
\int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}
\end{equation}
onde $a$ e $b$ são constantes, tal que $a$ e $b$ $\in \mathbb{R}$ e $a \neq |b|$.
\begin{equation}
I=\int \cos(ax) \cos(bx)dx
\end{equation}
Das fórmulas de adição e subtração de arcos, obtemos uma identidade trigonométrica que transforma um produto de cossenos em uma soma:
\begin{equation}
\cos(m+n) = \cos(m)\cos(n) - \text{sen}(m)\text{sen}(n)
\end{equation}
e
\begin{equation}
\cos(m-n) = \cos(m)\cos(n) + \text{sen}(m)\text{sen}(n)
\end{equation}
Somando $(3)$ e $(4)$, obtemos:
\begin{equation}
\cos(m-n)+\cos(m+n)= 2\cos(m)\cos(n)
\end{equation}
O que nos leva a:
\begin{equation}
\cos(m)\cos(n) = \frac{1}{2} \cos(m-n) + \frac{1}{2} \cos(m+n)
\end{equation}
Fazendo $m=ax$ e $n=bx$, temos que:
\begin{equation}
\cos(ax)\cos(bx) = \frac{1}{2} \cos[(a-b)x] + \frac{1}{2} \cos[(a+b)x]
\end{equation}
Substituindo na integral $(2)$, obtemos:
\begin{equation}
I = \frac{1}{2} \int \left[ \cos[(a-b)x] + \cos[(a+b)x] \right] dx
\end{equation}
Integrando termo a termo:
\begin{equation}
I = \frac{1}{2} \int \cos[(a-b)x] dx + \frac{1}{2} \int \cos[(a+b)x] dx
\end{equation}
Para o integrando $\cos[(a-b)x]$, fazemos a substituição $u=(a-b)x$. Assim, $du=(a-b)dx$ e $\displaystyle dx=\frac{du}{a-b}$. E para o integrando $cos[(a+b)x]$, fazemos a substituição $v=(a+b)x$. Assim $dv=(a+b)dx$ e $\displaystyle dx=\frac{dv}{a+b}$.
A integral fica:
\begin{equation}
I = \frac{1}{2(a-b)}\int \cos(u)du + \frac{1}{2(a+b)} \int \cos(v)dv
\end{equation}
A integral de $\cos(\theta) = \text{sen}(\theta)$. Assim:
\begin{gather}
I = \frac{1}{2(a-b)} \cdot \text{sen}(u) + \frac{1}{2(a+b)} \text{sen}(v) +C\\
I = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)} + C
\end{gather}
Método de integração por substituição
Adição e subtração de arcos

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
Matemática
Integral indefinida do produto de cossenos de monômios de coeficientes angulares diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios.

Vamos demonstrar que:
\begin{equation}
\int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}
\end{equation}
onde $a$ e $b$ são constantes, tal que $a$ e $b$ $\in \mathbb{R}$ e $a \neq |b|$.
Demonstração:
Seja a integral:\begin{equation}
I=\int \cos(ax) \cos(bx)dx
\end{equation}
Das fórmulas de adição e subtração de arcos, obtemos uma identidade trigonométrica que transforma um produto de cossenos em uma soma:
\begin{equation}
\cos(m+n) = \cos(m)\cos(n) - \text{sen}(m)\text{sen}(n)
\end{equation}
e
\begin{equation}
\cos(m-n) = \cos(m)\cos(n) + \text{sen}(m)\text{sen}(n)
\end{equation}
Somando $(3)$ e $(4)$, obtemos:
\begin{equation}
\cos(m-n)+\cos(m+n)= 2\cos(m)\cos(n)
\end{equation}
O que nos leva a:
\begin{equation}
\cos(m)\cos(n) = \frac{1}{2} \cos(m-n) + \frac{1}{2} \cos(m+n)
\end{equation}
Fazendo $m=ax$ e $n=bx$, temos que:
\begin{equation}
\cos(ax)\cos(bx) = \frac{1}{2} \cos[(a-b)x] + \frac{1}{2} \cos[(a+b)x]
\end{equation}
Substituindo na integral $(2)$, obtemos:
\begin{equation}
I = \frac{1}{2} \int \left[ \cos[(a-b)x] + \cos[(a+b)x] \right] dx
\end{equation}
Integrando termo a termo:
\begin{equation}
I = \frac{1}{2} \int \cos[(a-b)x] dx + \frac{1}{2} \int \cos[(a+b)x] dx
\end{equation}
Para o integrando $\cos[(a-b)x]$, fazemos a substituição $u=(a-b)x$. Assim, $du=(a-b)dx$ e $\displaystyle dx=\frac{du}{a-b}$. E para o integrando $cos[(a+b)x]$, fazemos a substituição $v=(a+b)x$. Assim $dv=(a+b)dx$ e $\displaystyle dx=\frac{dv}{a+b}$.
A integral fica:
\begin{equation}
I = \frac{1}{2(a-b)}\int \cos(u)du + \frac{1}{2(a+b)} \int \cos(v)dv
\end{equation}
A integral de $\cos(\theta) = \text{sen}(\theta)$. Assim:
\begin{gather}
I = \frac{1}{2(a-b)} \cdot \text{sen}(u) + \frac{1}{2(a+b)} \text{sen}(v) +C\\
I = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)} + C
\end{gather}
Veja mais:
Integral indefinida do produto de senos de monômios de coeficientes angulares diferentesMétodo de integração por substituição
Adição e subtração de arcos

- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
