Matemática

Algumas Observações Sobre a Notação de Derivada

No Cálculo, notações diferentes para a derivada é um fato e cada uma delas é de uso comum e as utilizamos conforme as circunstâncias em que os símbolos estão sendo usados. Então o que nos importa quais símbolos utilizamos se todos servem para o mesma coisa? Essa é uma questão de grande importância. Pois boas notações podem suavizar o caminho e realizar boa parte de nosso trabalho, enquanto notações ruins imobilizam, sendo quase impossível uma movimentação fácil.

A derivada de uma função $f(x)$ pode ser denotada por $f \prime (x)$:

$\displaystyle f^ \prime (x)=\lim_{\Delta x \rightarrow0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $

Essa notação tem o mérito de enfatizar que a derivada $f(x)$ é uma outra função de $x$ que está associada de certa maneira com a função dada. Se a função é dada na forma $y=f(x)$, com a variável dependente explícita, então o símbolo $y^\prime$ é utilizado no lugar de $f^\prime (x)$.

A principal desvantagem da notação prima $ \left (^\prime \right )$ para derivadas é que ela não sugere a natureza do processo pelo qual $f^\prime (x)$ foi obtida de $f(x)$, A notação de Leibniz é melhor nesse aspecto bem como em outros.

Para explicar a notação de Leibniz, começamos com uma função $y=f(x)$ e escrevemos o quociente de diferenças

$\displaystyle \frac{f(x+\Delta x)-f(x)}{\Delta x}$

na forma

$\displaystyle \frac{\Delta y}{\Delta x}$

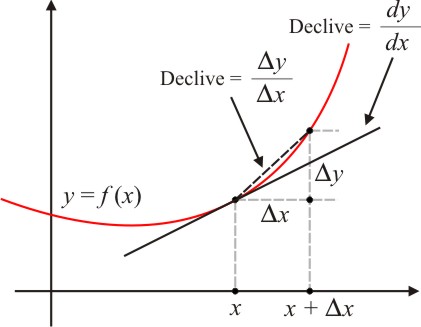
Onde $\Delta y=f(x+\Delta x)-f(x)$. Aqui $\Delta y$ não é simplesmente uma mudança qualquer em $y$; ela é a mudança específica que resulta quando a variável independente muda de $x$ para $x+\Delta x$. O quociente de diferenças $\Delta y / \Delta x$ pode ser interpretado como a razão da variação de $y$ pela variação de $x$ ao longo de uma curva $y=f(x)$, que representada o declive da secante.

[Figura 1]

Leibniz escreveu o limite desse quociente de diferenças, que naturalmente é a derivada $f^\prime (x)$, na forma $dy/dx$ (Leia “$dy$” sobre “$dx$” ou simplesmente “$dy,dx$”). Nesta notação, a definição de derivada assume a forma:

$\displaystyle \frac{dy}{dx} = \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} \qquad (1)$

e este é o coeficiente angular (declive) da tangente na figura 1. Outras duas formas equivalentes um pouco diferentes de $dy/dx$ são:

$\displaystyle \frac{df(x)}{dx}$ e $\displaystyle \frac{d}{dx}f(x)$

O símbolo $d/dx$ pode ser lido como “a derivada em relação a $x$ de ...”, qualquer que seja a função $x$ que siga.

Devemos compreender que $dy/dx$ dado em (1) é um símbolo individual e não um quociente entre duas quantidades, porque $dy$ e $dx$ não foram definidas e não tem existência independente.

Na notação de Leibniz, a formação do limite à direita de (1) é simbolicamente expressa substituindo a letra $\Delta$ pela letra $d$. Desse ponto de vista, o símbolo $dy/dx$ para a derivada tem a vantagem psicológica de nos fazer lembrar rapidamente de todo o processo de se formar o quociente de diferenças $\Delta y/\Delta x$ e calcular seu limite quando $\Delta \rightarrow 0$. A vantagem prática da notação de Leibniz é que para certas fórmulas fundamentais são mais fáceis de serem lembradas.

Mas por melhor que seja esta notação, não é perfeita. Suponha que queiramos escrever o valor numérico da derivada num ponto específico, como por exemplo 1. Como a notação $dy/dx$ não mostra a variável $x$ de maneira conveniente, como acontece quando usamos a notação $f^\prime (x)$, como forçados a usar uma notação desajeitada, como:

$\displaystyle \left ( \frac{dy}{dx} \right )_{x=1}$ ou $\displaystyle \frac{dy}{dx}\mid _{x=1}$

O símbolo ideal para esta representação é $f^\prime (1)$.

Cada notação é boa à sua maneira, dependendo do contexto na qual está inserida. Todas são amplamente utilizadas na Matemática e nas Ciências adjacentes.

Referências:

[1] Cálculo com Geometria Analítica V1 - Simmons - Editora McGraw Hill

Veja mais:

Os Mitos Leibzinianos a Respeito das Curvas Diferenciais
Leibniz e as Diferenciais
Curvas Contínuas Sem Derivadas

- Funções Compostas E A Regra Da Cadeia
A regra da cadeia é uma fórmula para a derivada da função composta de duas ou mais funções. Desenvolvida por Gottfried Leibniz, a regra da cadeia teve grande importância para o avanço do cálculo diferencial. Seu desenvolvimento foi devido à...

- Usando Derivadas Para Aproximar Funções
O simples fato geométrico de que a tangente a uma curva é uma boa aproximação da curva próximo ao ponto de tangência $P$, pode ser usado para obter valores aproximados de funções. [Figura 1] Vamos estimar o valor de uma função $f(x)$ quando...

- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...

- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...

- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...

Matemática