Matemática
Os egípcios antigos já empregavam linguagem simbólica para representar duas operações aritméticas: a soma era representada por duas pernas caminhando na direção da escrita e a subtração por pernas no sentido oposto.
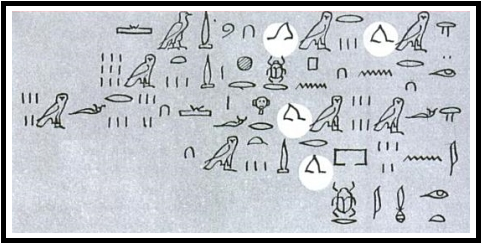
Ahmes ensina como calcular a área do círculo. Sem justificar, ele diz que tal área é igual à área de um quadrado cujo lado é $8/9$ do diâmetro do círculo. Em linguagem moderna é o mesmo que dizer que $\pi = 3,1605$, uma ótima aproximação para a época.
A figura que Ahmes utilizou não foi um círculo, mas sim um octógono:

O lado do quadrado circunscrito ao octógono mede $D$, que também é o diâmetro do círculo circunscrito ao mesmo quadrado e sobreposto ao octógono.
Então, a área do quadrado será dada por:
\begin{equation}
A_{Quadrado} = D^2
\end{equation}
Dividindo-se cada lado do quadrado em $3$ partes, podemos formar um octógono. A área de cada triângulo formado pelos vértices do quadrado será dada por:
\begin{equation}
A_{Triângulo} = \frac{\displaystyle \frac{1}{3}D \cdot \frac{1}{3}D}{2}= \frac{1}{18}D^2
\end{equation}
Assim, a área do octógono é a diferença entre a área do quadrado e dos quatro triângulos:
\begin{equation}
A_{Octógono} = D^2- 4\cdot \frac{1}{18}D^2\\
A_{Octógono} = \frac{7}{9}D^2
\end{equation}
Se o círculo tem diâmetro $D = 9$, logo a área do octógono será igual a $63$. Ahmes, então, aproximou este valor para $64$, que é um quadrado perfeito:
\begin{equation*}
63 \approx 64
\end{equation*}
Em notações modernas, temos que a área do círculo é dada por:
\begin{equation}
A_C = \pi r^2
\end{equation}
E assim, a área do octógono de diâmetro $D = 9$, cuja área se aproxima a de um quadrado de lado igual a $8$, pode ser escrita como:
\begin{equation}
A_C = \pi r^2\\
64 \approx \pi \left(\frac{9}{2}\right)^2\\
\pi \approx 3,1605
\end{equation}
Que é foi uma ótima aproximação para a época. Desta forma, os egípcios anteciparam-se aos gregos em mais de um milênio na ideia correta de aproximar um círculo por meio de polígonos. Na introdução de seu papiro, Ahmes diz basear-se em antigos escritos que hoje os historiadores acreditam ser datados de $1900 a.C.$.
[2] Notas de aula
Uma Breve Cronologia de PI
O Seqt de uma Pirâmide

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int \frac{1}{ax+b}\ Dx$
Nesta postagem vermos que: \begin{equation*} \int \frac{1}{ax+b}\ dx = \frac{1}{a}\ln |ax+b| + C \end{equation*} onde $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq 0$. [Família de funções integráveis do tipo $\displaystyle \frac{1}{ax+b}$] Seja a integral:...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
Matemática
Aproximação de PI pelos Egípcios
Os egípcios antigos já empregavam linguagem simbólica para representar duas operações aritméticas: a soma era representada por duas pernas caminhando na direção da escrita e a subtração por pernas no sentido oposto.

Ahmes ensina como calcular a área do círculo. Sem justificar, ele diz que tal área é igual à área de um quadrado cujo lado é $8/9$ do diâmetro do círculo. Em linguagem moderna é o mesmo que dizer que $\pi = 3,1605$, uma ótima aproximação para a época.
A figura que Ahmes utilizou não foi um círculo, mas sim um octógono:

O lado do quadrado circunscrito ao octógono mede $D$, que também é o diâmetro do círculo circunscrito ao mesmo quadrado e sobreposto ao octógono.
Então, a área do quadrado será dada por:
\begin{equation}
A_{Quadrado} = D^2
\end{equation}
Dividindo-se cada lado do quadrado em $3$ partes, podemos formar um octógono. A área de cada triângulo formado pelos vértices do quadrado será dada por:
\begin{equation}
A_{Triângulo} = \frac{\displaystyle \frac{1}{3}D \cdot \frac{1}{3}D}{2}= \frac{1}{18}D^2
\end{equation}
Assim, a área do octógono é a diferença entre a área do quadrado e dos quatro triângulos:
\begin{equation}
A_{Octógono} = D^2- 4\cdot \frac{1}{18}D^2\\
A_{Octógono} = \frac{7}{9}D^2
\end{equation}
Se o círculo tem diâmetro $D = 9$, logo a área do octógono será igual a $63$. Ahmes, então, aproximou este valor para $64$, que é um quadrado perfeito:
\begin{equation*}
63 \approx 64
\end{equation*}
Em notações modernas, temos que a área do círculo é dada por:
\begin{equation}
A_C = \pi r^2
\end{equation}
E assim, a área do octógono de diâmetro $D = 9$, cuja área se aproxima a de um quadrado de lado igual a $8$, pode ser escrita como:
\begin{equation}
A_C = \pi r^2\\
64 \approx \pi \left(\frac{9}{2}\right)^2\\
\pi \approx 3,1605
\end{equation}
Que é foi uma ótima aproximação para a época. Desta forma, os egípcios anteciparam-se aos gregos em mais de um milênio na ideia correta de aproximar um círculo por meio de polígonos. Na introdução de seu papiro, Ahmes diz basear-se em antigos escritos que hoje os historiadores acreditam ser datados de $1900 a.C.$.
Referências:
[1] Introdução à História da Matemática - Howard Eves - Ed. Unicamp[2] Notas de aula
Veja mais:
Newton e a Série Infinita para PIUma Breve Cronologia de PI
O Seqt de uma Pirâmide

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int \frac{1}{ax+b}\ Dx$
Nesta postagem vermos que: \begin{equation*} \int \frac{1}{ax+b}\ dx = \frac{1}{a}\ln |ax+b| + C \end{equation*} onde $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq 0$. [Família de funções integráveis do tipo $\displaystyle \frac{1}{ax+b}$] Seja a integral:...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
