Matemática
\overline{MN}=b_M=\frac{b+b'}{2}=\frac{\overline{AB}+\overline{CD}}{2}
\end{equation}
\overline{PN}=\frac{1}{2} \overline{AB}
\end{equation}
Analogamente, no triângulo $ACD$, temos que $\overline{MP}$ é sua base média, dada por:
\begin{equation}
\overline{MP}=\frac{1}{2} \overline{CD}
\end{equation}
Veja aqui a demonstração da base média de um triângulo.
Temos ainda que:
\begin{equation}
\overline{MN}=\overline{MP}+\overline{PN}
\end{equation}
Substituindo $(2)$ e $(3)$ em $(4)$, obtemos:
\begin{equation}
\overline{MN}=\frac{1}{2}\overline{AB}+\frac{1}{2}\overline{CD}=\frac{\overline{AB}+\overline{CD}}{2}
\end{equation}
Aplicando a fórmula da base média do trapézio, dada em $(5)$, temos:
$$\overline{MN}=\frac{12+8}{2}=10cm$$

Vamos representar a escada com o diagrama simplificado abaixo:
Com os dados iniciais do problema, os segmentos $\overline{AA'}=45cm$ e $\overline{II'}=30cm$. Notem que o segmento $\overline{EE'}$ é a base média do trapézio $AA'I'I$. Assim:
$$\overline{EE'}=\frac{\overline{AA'}+\overline{II'}}{2}=\frac{45+30}{2}=37,5cm$$
Agora, vamos aplicar a fórmula para determinar as medidas dos demais degraus.
$$\overline{CC'}=\frac{\overline{AA'}+\overline{CC'}}{2}=\frac{45+37,5}{2}=41,25cm$$
$$\overline{BB'}=\frac{\overline{AA'}+\overline{CC'}}{2}=\frac{45+41,25}{2}=43,125cm$$
$$\overline{DD'}=\frac{\overline{CC'}+\overline{EE'}}{2}=\frac{41,25+37,5}{2}=39,375cm$$
$$\overline{GG'}=\frac{\overline{EE'}+\overline{II'}}{2}=\frac{37,5+30}{2}=33,75cm$$
$$\overline{FF'}=\frac{\overline{EE'}+\overline{GG'}}{2}=\frac{37,5+33,75}{2}=35,625cm$$
$$\overline{HH'}=\frac{\overline{GG'}+\overline{II'}}{2}=\frac{33,75+30}{2}=31,875cm$$
Referências:
[1] Geometria 1 - Morgado
[2] Elementos de Geometria e Desenho Geométrico V1 - Putnoki
[3] Fundamentos de Matemática Elementar V9 - Geometria Plana - Osvaldo Dolce & Nicolau Pompeo
Veja mais:
Organograma dos Quadriláteros Notáveis
Base Média de um Triângulo
Quadriláteros Notáveis

- Baricentro
As três medianas de um triângulo interceptam-se num mesmo ponto que divide cada mediana em duas partes tais que a parte que contém o vértice é o dobro da outra. Se $$\overline{AM_1}\text{,}\overline{BM_2}\text{,}\overline{CM_3}$$ são as medianas...
- Teorema Do Quadrilátero Circunscritível
Este artigo trata do quadrilátero circunscrito a uma circunferência. Veremos a condição necessária e suficiente, algumas propriedades e teoremas interessantes e alguns exercícios resolvidos. Teorema $1$:Se conduzirmos por um ponto $P$ os segmentos...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Base Média de um Trapézio
O trapézio é um quadrilátero plano convexo e é considerado notável por possuir algumas propriedades interessantes. Uma delas é a propriedade da base média do trapézio, que é a semi-soma das bases do trapézio.

Definição $1$: Trapézio é todo quadrilátero que possui um par, e somente um par, de lados opostos paralelos.
Os lados opostos paralelos são denominados por bases e os lados opostos transversos são denominados apenas por lados.
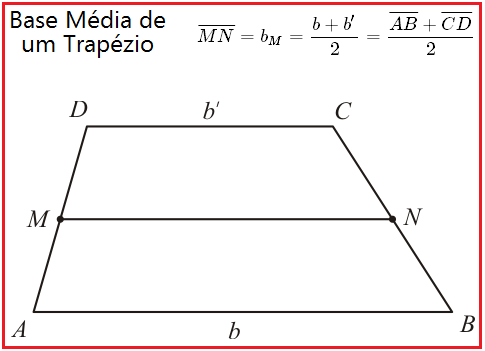
Definição $2$: Base média de um trapézio é o segmento que une os pontos médios dos lados do trapézio.
Seja o trapézio $ABCD$, cujos segmentos $\overline{AB}$ e $\overline{CD}$ são suas bases paralelas. Sejam $M$ e $N$ os pontos médios dos lados do trapézio. O segmento $\overline{MN}$ é a base média do trapézio e é expresso por:
\begin{equation}\overline{MN}=b_M=\frac{b+b'}{2}=\frac{\overline{AB}+\overline{CD}}{2}
\end{equation}
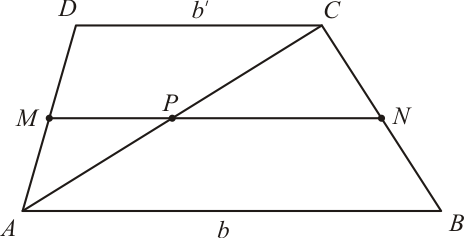
Para demonstrar esta propriedade, vamos partir do pressuposto que os pontos $M$ e $N$ são os pontos médios do lados do trapézio.
Traçando a diagonal $\overline{AC}$, cortando o segmento $\overline{MN}$ em $P$, obtemos os triângulos $ABC$ e $ACD$. Do triângulo $ABC$, o segmento $\overline{PN}$ é paraleo à $\overline{AB}$. Sendo $N$ o ponto médio de $\overline{BC}$, $P$ é o ponto médio de $\overline{AC}$. Logo $\overline{PN}$ é a base média do triângulo $ABC$ e é dada por:
\begin{equation}\overline{PN}=\frac{1}{2} \overline{AB}
\end{equation}
Analogamente, no triângulo $ACD$, temos que $\overline{MP}$ é sua base média, dada por:
\begin{equation}
\overline{MP}=\frac{1}{2} \overline{CD}
\end{equation}
Veja aqui a demonstração da base média de um triângulo.
Temos ainda que:
\begin{equation}
\overline{MN}=\overline{MP}+\overline{PN}
\end{equation}
Substituindo $(2)$ e $(3)$ em $(4)$, obtemos:
\begin{equation}
\overline{MN}=\frac{1}{2}\overline{AB}+\frac{1}{2}\overline{CD}=\frac{\overline{AB}+\overline{CD}}{2}
\end{equation}
Exemplo $1$: Em um trapézio de bases $\overline{AB}=12cm$ e $\overline{CD}=8cm$, calcule sua base média $\overline{MN}$, sendo $M$ e $N$ os pontos médis de seus lados.
Aplicando a fórmula da base média do trapézio, dada em $(5)$, temos:
$$\overline{MN}=\frac{12+8}{2}=10cm$$
Exemplo $2$: Uma aplicação interessante é em escadas. Considere a escada da imagem abaixo com $9$ degraus, sendo o primeiro degrau com $45cm$ de largura e o último degrau com $30cm$ de largura. Calcular as larguras dos demais degraus.

Uma escada pode ser considerada como um trapézio. Se esta contiver um número ímpar de degraus, basta sabermos quanto mede o primeiro e o último para calcularmos a medida do degrau médio (informação extremamente útil para os matemáticos!), desde que as distâncias entre os degraus sejam constantes. A escada que tenho em minha casa, tem $7$ degraus com $25cm$ de distância entre eles, mas vi na internet outras com $30cm$.
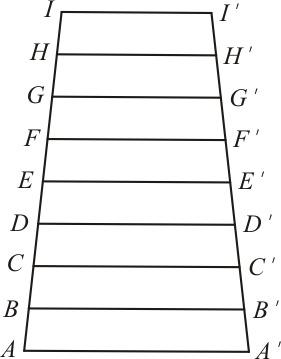
Vamos representar a escada com o diagrama simplificado abaixo:

Com os dados iniciais do problema, os segmentos $\overline{AA'}=45cm$ e $\overline{II'}=30cm$. Notem que o segmento $\overline{EE'}$ é a base média do trapézio $AA'I'I$. Assim:
$$\overline{EE'}=\frac{\overline{AA'}+\overline{II'}}{2}=\frac{45+30}{2}=37,5cm$$
Agora, vamos aplicar a fórmula para determinar as medidas dos demais degraus.
$$\overline{CC'}=\frac{\overline{AA'}+\overline{CC'}}{2}=\frac{45+37,5}{2}=41,25cm$$
$$\overline{BB'}=\frac{\overline{AA'}+\overline{CC'}}{2}=\frac{45+41,25}{2}=43,125cm$$
$$\overline{DD'}=\frac{\overline{CC'}+\overline{EE'}}{2}=\frac{41,25+37,5}{2}=39,375cm$$
$$\overline{GG'}=\frac{\overline{EE'}+\overline{II'}}{2}=\frac{37,5+30}{2}=33,75cm$$
$$\overline{FF'}=\frac{\overline{EE'}+\overline{GG'}}{2}=\frac{37,5+33,75}{2}=35,625cm$$
$$\overline{HH'}=\frac{\overline{GG'}+\overline{II'}}{2}=\frac{33,75+30}{2}=31,875cm$$
Referências:
[1] Geometria 1 - Morgado
[2] Elementos de Geometria e Desenho Geométrico V1 - Putnoki
[3] Fundamentos de Matemática Elementar V9 - Geometria Plana - Osvaldo Dolce & Nicolau Pompeo
Veja mais:
Organograma dos Quadriláteros Notáveis
Base Média de um Triângulo
Quadriláteros Notáveis

- Baricentro
As três medianas de um triângulo interceptam-se num mesmo ponto que divide cada mediana em duas partes tais que a parte que contém o vértice é o dobro da outra. Se $$\overline{AM_1}\text{,}\overline{BM_2}\text{,}\overline{CM_3}$$ são as medianas...
- Teorema Do Quadrilátero Circunscritível
Este artigo trata do quadrilátero circunscrito a uma circunferência. Veremos a condição necessária e suficiente, algumas propriedades e teoremas interessantes e alguns exercícios resolvidos. Teorema $1$:Se conduzirmos por um ponto $P$ os segmentos...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
