Matemática

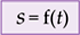

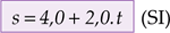

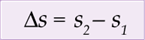
- Cinética Escalar
A cinética escalar é um ramo das partes da mecânica que estuda o movimento dos corpos sem se importar com suas causas. Ela está dividida em: Ponto Material: são os corpos que possuem dimensões incapazes de interferir em estudos de determinado fenômeno....
- Cinematica Parte Ii
Vimos que, quando um objeto está em movimento, ele muda de posição ao longo de sua trajetória. A cada posição do objeto, associamos um espaço (s), e a variação de espaço representa o deslocamento escalar (s). A tal variação de espaço ocorre...
- Movimento RetilÍneo Uniforme (mru)
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com...
- Movimento Uniformemente Variado
O movimento uniformemente variado é o movimento no qual a velocidade escalar varia uniformemente no decorrer do tempo. Quando se observa que a velocidade de uma partícula é uniforme, independentemente de sua trajetória, diz-se que a partícula possui...
- Movimento Uniforme
Pense em um automóvel que está em uma determinada estrada se movendo a uma velocidade constante tal que seu velocímetro indica 60 km/h. Tal situação não parece ser realidade, pois todo automóvel muda sua velocidade constantemente, seja para ultrapassar...
Matemática
Cinematica parte I
1. Localização
Para localizarmos um móvel num determinado instante, construímos um sistema de referência cartesiana, que pode apresentar uma, duas ou três dimensões.
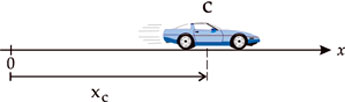
Para darmos a posição de um automóvel em trajetória retilínea, basta um único eixo (movimento unidimensional), já que uma abcissa x desse eixo o localizará num certo instante.

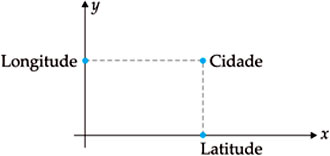
Para identificarmos uma cidade no nosso planeta, precisamos de um sistema cartesiano com dois eixos, x e y, determinando a sua latitude e longitude.

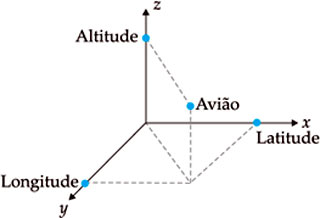
Agora, para identificarmos a posição de um avião em movimento na atmosfera, num determinado instante, precisamos de um sistema cartesiano com três eixos, x, y e z, determinando sua latitude, longitude e altitude.

2. Espaço
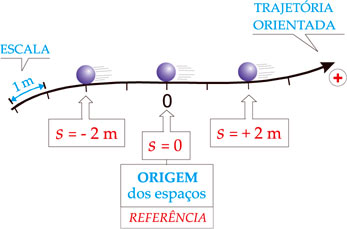
Quando conhecemos a trajetória descrita por um móvel, segundo um referencial, podemos dispensar o uso de eixos cartesianos e definir a posição do móvel ao longo da trajetória, tomando um ponto desta como referência. Este ponto de referência é denominado origem (O) e a posição do móvel, espaço (s).


O espaço (s) de um móvel nos fornece a sua localização na trajetória, em relação à origem dos espaços (s = 0). A distância do móvel à origem (O), medida ao longo da trajetória, é precedida de um sinal algébrico (+) ou (–) para indicar a região da trajetória: à direita ou à esquerda da origem, conforme a orientação escolhida para essa trajetória.
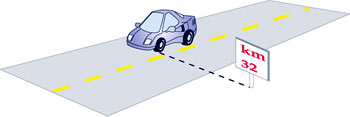
Um marco quilométrico de uma rodovia corresponde, na prática, à grandeza espaço.

Quando se diz que um carro está no km 32, isto indica que ele se posiciona a 32 km da origem (km 0) da rodovia.
3. Função Horária do Espaço
Durante o movimento de um ponto material, a sua posição varia com o decorrer do tempo. A maneira como a posição varia com o tempo é a lei do movimento ou função horária.
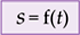
Na expressão acima, devemos ler:

As variáveis s e t têm unidades, que devem ser indicadas quando se representa a função. Normalmente são utilizadas as unidades do Sistema Internacional (SI), ou seja:
• espaço  metros (m)
metros (m)
 metros (m)
metros (m) • tempo  segundos (s)
segundos (s)
 segundos (s)
segundos (s) Exemplo
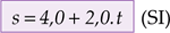
s e t são as variáveis, isto significa que para cada valor de t temos um valor de s.
No instante t = 0, o espaço s é denominado s0 (espaço inicial).
Assim:

4. Sentidos de Tráfego
| Quando o móvel caminha no sentido da orientação da trajetória, seus espaços (s) são crescentes no decorrer do tempo. Denominamos este sentido de tráfego de progressivo. | 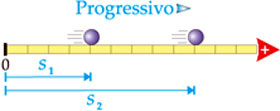 |
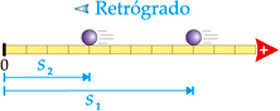 | Quando o móvel retrocede, caminhando contra a orientação da trajetória, seus espaços (s) são decrescentes. Este sentido de tráfego é classificado como retrógrado. |
5. Deslocamento Escalar
A grandeza física que indica, entre dois instantes, a variação de espaço do móvel é denominada deslocamento escalar ( s).
s).
 s).
s). 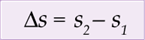

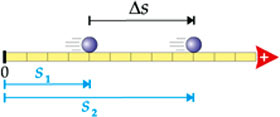
A figura abaixo apresenta os espaços ocupados por um móvel numa trajetória em dois instantes diferentes.
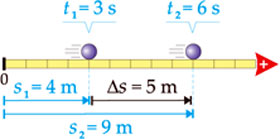 | Pela figura anterior, temos que, no instante t1 = 3s, o móvel encontra-se na posição s1 = 4 m, e, no instante t2 = 6 s, sua posição é s2 = 9 m. Podemos afirmar que, entre os instantes 3 s e 6 s, o espaço do móvel variou de 5 m, ou seja, de 4 para 9 m. Essa variação de espaço recebe o nome de deslocamento escalar (  s). s).Quando o movimento for progressivo, o deslocamento escalar será positivo (  s > 0). Quando retrógrado, será negativo ( s > 0). Quando retrógrado, será negativo ( s < 0). s < 0). |
6. Distância Percorrida
Distância percorrida (d) é a grandeza que nos informa quanto o móvel efetivamente percorreu entre dois instantes.
Quando o sentido de tráfego do móvel se mantém, seja progressivo ou retrógrado, a distância percorrida coincide com o módulo do deslocamento escalar ocorrido.
Na figura a seguir, considerando-se o movimento como progressivo, a distância percorrida entre os instantes t1 e t2 foi de 5 m. Ou seja: d = | s| = | 5 m | = 5 m s| = | 5 m | = 5 m | 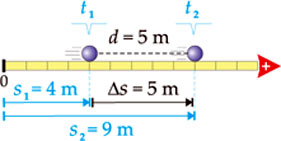 |
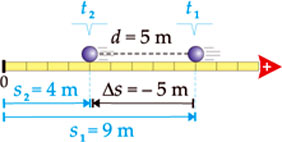 | Caso o sentido de tráfego entre t1 e t2 fosse retrógrado, como ilustra a figura ao lado, o deslocamento escalar seria de - 5 m e a distância percorrida: d = |  s| = | – 5 m | = 5 m. s| = | – 5 m | = 5 m. |
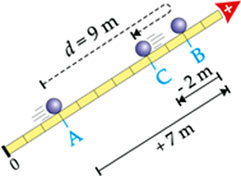
Quando há inversão de sentido no tráfego, a distância total percorrida é calculada somando-se os módulos dos deslocamentos parciais (em cada sentido). O trajeto ABC sobre a rampa abaixo exemplifica este caso, sendo B o ponto de inversão de tráfego.

www.vestibulandoweb.com.br
- Cinética Escalar
A cinética escalar é um ramo das partes da mecânica que estuda o movimento dos corpos sem se importar com suas causas. Ela está dividida em: Ponto Material: são os corpos que possuem dimensões incapazes de interferir em estudos de determinado fenômeno....
- Cinematica Parte Ii
Vimos que, quando um objeto está em movimento, ele muda de posição ao longo de sua trajetória. A cada posição do objeto, associamos um espaço (s), e a variação de espaço representa o deslocamento escalar (s). A tal variação de espaço ocorre...
- Movimento RetilÍneo Uniforme (mru)
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com...
- Movimento Uniformemente Variado
O movimento uniformemente variado é o movimento no qual a velocidade escalar varia uniformemente no decorrer do tempo. Quando se observa que a velocidade de uma partícula é uniforme, independentemente de sua trajetória, diz-se que a partícula possui...
- Movimento Uniforme
Pense em um automóvel que está em uma determinada estrada se movendo a uma velocidade constante tal que seu velocímetro indica 60 km/h. Tal situação não parece ser realidade, pois todo automóvel muda sua velocidade constantemente, seja para ultrapassar...
