Matemática
 Pontos exteriores: Os pontos exteriores a um círculo são os pontos localizados fora do círculo.
Pontos exteriores: Os pontos exteriores a um círculo são os pontos localizados fora do círculo.
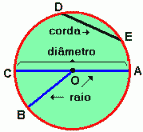 Corda: Corda de uma circunferência é um segmento de reta cujas extremidades pertencem à circunferência. Na figura, os segmentos de reta AC e DE são cordas.
Corda: Corda de uma circunferência é um segmento de reta cujas extremidades pertencem à circunferência. Na figura, os segmentos de reta AC e DE são cordas.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência. Na figura, o segmento de reta AC é um diâmetro.
 Reta tangente: Uma reta tangente a uma circunferência é uma reta que intercepta a circunferência em um único ponto P. Este ponto é conhecido como ponto de tangência ou ponto de contato. Na figura ao lado, o ponto P é o ponto de tangência e a reta que passa pelos pontos E e F é uma reta tangente à circunferência.
Reta tangente: Uma reta tangente a uma circunferência é uma reta que intercepta a circunferência em um único ponto P. Este ponto é conhecido como ponto de tangência ou ponto de contato. Na figura ao lado, o ponto P é o ponto de tangência e a reta que passa pelos pontos E e F é uma reta tangente à circunferência.
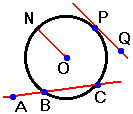 Tangentes e secantes são nomes de retas, mas também são usados para denotar segmentos de retas ou semi-retas. Por exemplo, "A tangente PQ" pode significar a reta tangente à circunferência que passa pelos pontos P e Q mas também pode ser o segmento de reta tangente à circunferência que liga os pontos P e Q. Do mesmo modo, a "secante AC" pode significar a reta que contém a corda BC e também pode ser o segmento de reta ligando o ponto A ao ponto C.
Tangentes e secantes são nomes de retas, mas também são usados para denotar segmentos de retas ou semi-retas. Por exemplo, "A tangente PQ" pode significar a reta tangente à circunferência que passa pelos pontos P e Q mas também pode ser o segmento de reta tangente à circunferência que liga os pontos P e Q. Do mesmo modo, a "secante AC" pode significar a reta que contém a corda BC e também pode ser o segmento de reta ligando o ponto A ao ponto C.
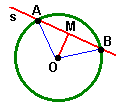 Se uma reta s, secante a uma circunferência de centro O, intercepta a circunferência em dois pontos distintos A e B, a perpendicular à reta s que passa pelo centro O da circunferência, passa também pelo ponto médio da corda AB.
Se uma reta s, secante a uma circunferência de centro O, intercepta a circunferência em dois pontos distintos A e B, a perpendicular à reta s que passa pelo centro O da circunferência, passa também pelo ponto médio da corda AB.
 Seja OP um raio de uma circunferência, onde O é o centro e P um ponto da circunferência. Toda reta perpendicular ao raio OP é tangente à circunferência no ponto de tangência P.
Seja OP um raio de uma circunferência, onde O é o centro e P um ponto da circunferência. Toda reta perpendicular ao raio OP é tangente à circunferência no ponto de tangência P.
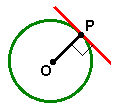 Toda reta tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
Toda reta tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
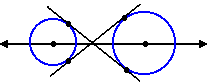
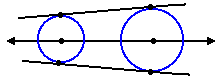
Ao traçar uma reta ligando os centros de duas circunferências no plano, esta reta separa o plano em dois semi-planos. Se os pontos de tangência, um em cada circunferência, estão no mesmo semi-plano, temos uma reta tangente comum externa. Se os pontos de tangência, um em cada circunferência, estão em semi-planos diferentes, temos uma reta tangente comum interna.

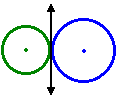
 As circunferências são tangentes externas uma à outra se os seus centros estão em lados opostos da reta tangente comum e elas são tangentes internas uma à outra se os seus centros estão do mesmo lado da reta tangente comum.
As circunferências são tangentes externas uma à outra se os seus centros estão em lados opostos da reta tangente comum e elas são tangentes internas uma à outra se os seus centros estão do mesmo lado da reta tangente comum.
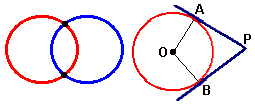 Circunferências secantes: são aquelas que possuem somente dois pontos distintos em comum.
Circunferências secantes: são aquelas que possuem somente dois pontos distintos em comum.
Segmentos tangentes: Se AP e BP são segmentos de reta tangentes à circunferência nos ponto A e B, então esses segmentos AP e BP são congruentes.
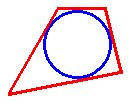
 Propriedade dos quadriláteros circunscritos: Se um quadrilátero é circunscrito a uma circunferência, a soma de dois lados opostos é igual a soma dos outros dois lados.
Propriedade dos quadriláteros circunscritos: Se um quadrilátero é circunscrito a uma circunferência, a soma de dois lados opostos é igual a soma dos outros dois lados.


 A medida da semicircunferência é 180 graus ou Pi radianos.
A medida da semicircunferência é 180 graus ou Pi radianos.
Em circunferências congruentes ou em uma simples circunferência, arcos que possuem medidas iguais são arcos congruentes.
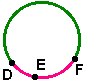 Em uma circunferência, se um ponto E está entre os pontos D e F, que são extremidades de um arco menor, então: m(DE)+m(EF)=m(DF).
Em uma circunferência, se um ponto E está entre os pontos D e F, que são extremidades de um arco menor, então: m(DE)+m(EF)=m(DF).
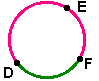 Se o ponto E está entre os pontos D e F, extremidades de um arco maior: m(DE)+m(EF)=m(DEF).
Se o ponto E está entre os pontos D e F, extremidades de um arco maior: m(DE)+m(EF)=m(DEF).
Apenas esta última relação faz sentido para as duas últimas figuras apresentadas.
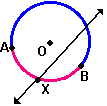
Para obter a distância de um ponto O a uma reta r, traçamos uma reta perpendicular à reta dada passando pelo ponto O. O ponto T obtido pela interseção dessas duas retas é o ponto que determinará um extremo do segmento OT cuja medida representa a distância entre o ponto e a reta.
Em uma mesma circunferência ou em circunferências congruentes, cordas congruentes possuem arcos congruentes e arcos congruentes possuem cordas congruentes. (Situação 1).
Um diâmetro que é perpendicular a uma corda é bissetor da corda e também de seus dois arcos. (Situação 2).
Em uma mesma circunferência ou em circunferências congruentes, cordas que possuem a mesma distância do centro são congruentes. (Situação 3).

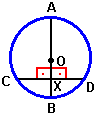




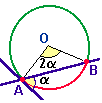
m = n/2 = (1/2) m(AB)

Pelo ponto A, trace uma reta t formando com o segmento AB um ângulo congruente a k (mesma medida que o ângulo k);
Traçar uma reta p perpendicular à reta t passando pelo ponto A;
Determinar o ponto médio M do segmento AB;
Traçar a reta mediatriz m ao segmento AB;
Obter o ponto O que é a interseção entre a reta p e a mediatriz m.
Com o compasso centrado no ponto O e abertura OA, traçar o arco de circunferência localizado acima do segmento AB.
O arco que aparece em vermelho no gráfico ao lado é o arco capaz.
Observação: Todo ângulo inscrito no arco capaz AB, com lados passando pelos pontos A e B são congruentes e isto significa que, o segmento de reta AB é sempre visto sob o mesmo ângulo de visão se o vértice deste ângulo está localizado no arco capaz. Na figura abaixo à esquerda, os ângulos que passam por A e B e têm vértices em V1, V2, V3, ..., são todos congruentes (a mesma medida).
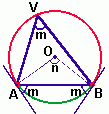
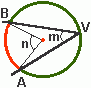
 Na figura acima à direita, o arco capaz relativo ao ângulo semi-inscrito m de vértice em A é o arco AVB. Se n é ângulo central então a medida de m é o dobro da medida de n, isto é:
Na figura acima à direita, o arco capaz relativo ao ângulo semi-inscrito m de vértice em A é o arco AVB. Se n é ângulo central então a medida de m é o dobro da medida de n, isto é:
m(arco AB) = 2 medida(m) = medida(n)
 Na sequência, usaremos a notação (PZ) para representar a medida do segmento PZ, em função das dificuldades que a linguagem HTML proporciona para a apresentação de materiais de Matemática.
Na sequência, usaremos a notação (PZ) para representar a medida do segmento PZ, em função das dificuldades que a linguagem HTML proporciona para a apresentação de materiais de Matemática.
Cordas interceptando dentro da circunferência: Se duas cordas de uma mesma circunferência se interceptam em um ponto P dentro da circunferência, então o produto das medidas das duas partes de uma corda é igual ao produto das medidas das duas partes da outra corda.

Se uma das retas passa pelos pontos A e B e a outra reta passa pelos pontos C e D da circunferência, então o produto da medida do segmento secante PA pela medida da sua parte exterior PB é igual ao produto da medida do segmento secante PC pela medida da sua parte exterior PD.


Desse modo, (PD).(PC)=(PA).(PB) e podemos escrever que x(14-x)=5×8, de onde segue que x²-14x+40=0. Resolvendo esta equação do segundo grau, obtemos: x=4 ou x=10, o que significa que se uma das partes do segmento medir 4cm, a outra medirá 10cm. Pela figura anexada, observamos que o segmento PD é maior que o segmento PC e concluímos que (PD)=10cm e (PC)=4cm.
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferência
CircunferênciaMarcos Noé Circunferência e seus elementosNo cotidiano identificamos objetos e construções que lembram uma circunferência, um contorno ou regiões circulares. A circunferência possui propriedades e definições...
- Posição Relativa Entre Uma Reta E Uma Circunferência
Posição relativa entre uma reta e uma circunferênciaMarcelo Rigonatto CircunferênciaConsidere uma circunferência no plano de cento O(xo, yo) e raio r. Dada uma reta s de equação ax + by +c = 0, também do mesmo plano. A reta...
- Circunferência
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br A importância da circunferênciaA...
- Construções Geométricas De Tangentes Com Régua E Compasso (parte 2)
Nesta segunda parte sobre construção de tangentes, vamos resolver três problemas clássicos sobre traçados de tangentes utilizando régua e compasso. 1) São dados dois pontos O e P e uma distância d. Conduzir uma reta por P que diste d de O. [Figura...
Matemática
CÍRCULO, CIRCUNFERÊNCIA E ARCOS
Circunferência e Círculo
Circunferência: A circunferência é o lugar geométrico de todos os pontos de um plano que estão localizados a uma mesma distância r de um ponto fixo denominado o centro da circunferência. Esta talvez seja a curva mais importante no contexto das aplicações.
Raio, corda e diâmetro
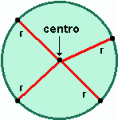
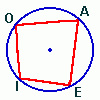
Raio: Raio de uma circunferência (ou de um círculo) é um segmento de reta com uma extremidade no centro da circunferência e a outra extremidade num ponto qualquer da circunferência. Na figura, os segmentos de reta OA, OB e OC são raios.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência. Na figura, o segmento de reta AC é um diâmetro.
Posições relativas de uma reta e uma circunferência
Reta secante: Uma reta é secante a uma circunferência se essa reta intercepta a circunferência em dois pontos quaisquer, podemos dizer também que é a reta que contém uma corda
Observações:
Raios e diâmetros são nomes de segmentos de retas mas às vezes são também usados como os comprimentos desses segmentos. Por exemplo, podemos dizer que ON é o raio da circunferência, mas é usual dizer que o raio ON da circunferência mede 10cm ou que o raio ON tem 10cm.
Propriedades das secantes e tangentes
Se uma reta s, secante a uma circunferência de centro O, intercepta a circunferência em dois pontos distintos A e B e se M é o ponto médio da corda AB, então o segmento de reta OM é perpendicular à reta secante s.


Posições relativas de duas circunferências
Reta tangente comum: Uma reta que é tangente a duas circunferências ao mesmo tempo é denominada uma tangente comum. Há duas possíveis retas tangentes comuns: a interna e a externa.Tangente comum interna

Tangente comum externa
Circunferências internas
Uma circunferência C1 é interna a uma circunferência C2, se todos os pontos do círculo C1 estão contidos no círculo C2. Uma circunferência é externa à outra se todos os seus pontos são pontos externos à outra.
Circunferências concêntricas
Duas ou mais circunferências com o mesmo centro mas com raios diferentes são circunferências concêntricas.Circunferências tangente
Duas circunferências que estão no mesmo plano, são tangentes uma à outra, se elas são tangentes à mesma reta no mesmo ponto de tangência.Circunf. tangentes externas

Circunf. tangentes internas


Segmentos tangentes: Se AP e BP são segmentos de reta tangentes à circunferência nos ponto A e B, então esses segmentos AP e BP são congruentes.
Polígonos circunscritos
Polígono circunscrito a uma circunferência é o que possui seus lados tangentes à circunferência. Ao mesmo tempo, dizemos que esta circunferência está inscrita no polígono.Quadrilátero circunscrito

Triângulo circunscrito

Arco de circunferência e ângulo central
Seja a circunferência de centro O traçada ao lado. Pela definição de circunferência temos que OP=OQ=OR=... e isto indica que os raios de uma circunferência são segmentos congruentes.Circunferências congruentes
São circunferências que possuem raios congruentes. Aqui a palavra raio refere-se ao segmento de reta e não a um número.
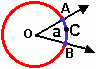
Ângulo central
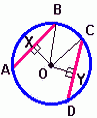
Em uma circunferência, o ângulo central é aquele cujo vértice coincide com o centro da circunferência. Na figura, o ângulo a é um ângulo central. Se numa circunferência de centro O, um ângulo central determina um arco AB, dizemos que AB é o arco correspondente ao ângulo AÔB.
Arco menor
É um arco que reúne dois pontos da circunferência que não são extremos de um diâmetro e todos os pontos da circunferência que estão dentro do ângulo central cujos lados contém os dois pontos. Na figura, a linha vermelha indica o arco menor AB ou arco menor ACB.Arco maior
É um arco que liga dois pontos da circunferência que não são extremos de um diâmetro e todos os pontos da circunferência que estão fora do ângulo central cujos lados contém os dois pontos. Na figura a parte azul é o arco maior, o ponto D está no arco maior ADB enquanto o ponto C não está no arco maior mas está no arco menor AB, assim é frequentemente usado três letras para representar o arco maior.
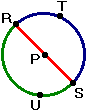
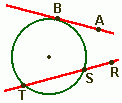
Semicircunferência
É um arco obtido pela reunião dos pontos extremos de um diâmetro com todos os pontos da circunferência que estão em um dos lados do diâmetro. O arco RTS é uma semicircunferência da circunferência de centro P e o arco RUS é outra.
Observações: Em uma circunferência dada, temos que:
A medida do arco menor é a medida do ângulo central correspondente a m(AÔB) e a medida do arco maior é 360 graus menos a medida do arco menor m(AÔB).
Em circunferências congruentes ou em uma simples circunferência, arcos que possuem medidas iguais são arcos congruentes.


Apenas esta última relação faz sentido para as duas últimas figuras apresentadas.
Propriedades de arcos e cordas
Uma corda de uma circunferência é um segmento de reta que une dois pontos da circunferência. Se os extremos de uma corda não são extremos de um diâmetro eles são extremos de dois arcos de circunferência sendo um deles um arco menor e o outro um arco maior. Quando não for especificada, a expressão arco de uma corda se referirá ao arco menor e quanto ao arco maior sempre teremos que especificar.
Observações
Se um ponto X está em um arco AB e o arco AX é congruente ao arco XB, o ponto X é o ponto médio do arco AB. Além disso, qualquer segmento de reta que contém o ponto X é um segmento bissetor do arco AB. O ponto médio do arco não é o centro do arco, o centro do arco é o centro da circunferência que contém o arco.Para obter a distância de um ponto O a uma reta r, traçamos uma reta perpendicular à reta dada passando pelo ponto O. O ponto T obtido pela interseção dessas duas retas é o ponto que determinará um extremo do segmento OT cuja medida representa a distância entre o ponto e a reta.
Em uma mesma circunferência ou em circunferências congruentes, cordas congruentes possuem arcos congruentes e arcos congruentes possuem cordas congruentes. (Situação 1).
Um diâmetro que é perpendicular a uma corda é bissetor da corda e também de seus dois arcos. (Situação 2).
Em uma mesma circunferência ou em circunferências congruentes, cordas que possuem a mesma distância do centro são congruentes. (Situação 3).
Situação 1

Situação 2

Situação 3

Polígonos inscritos na circunferência
Um polígono é inscrito em uma circunferência se cada vértice do polígono é um ponto da circunferência e neste caso dizemos que a circunferência é circunscrita ao polígono.


Propriedade dos quadriláteros inscritos
Se um quadrilátero está inscrito em uma circunferência então os ângulos opostos são suplementares, isto é a soma dos ângulos opostos é 180 graus e a soma de todos os quatro ângulos é 360 graus. + Î = 180 graus
Ê + Ô = 180 graus
 + Ê + Î + Ô = 360 graus
Ê + Ô = 180 graus
 + Ê + Î + Ô = 360 graus

Ângulos inscritos
Ângulo inscrito
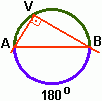
Relativo a uma circunferência é um ângulo com o vértice na circunferência e os lados secantes a ela. Na figura à esquerda abaixo, o ângulo AVB é inscrito e AB é o arco correspondente.

Medida do ângulo inscrito
A medida de um ângulo inscrito em uma circunferência é igual à metade da respectiva medida do ângulo central, ou seja, a metade de seu arco correspondente, isto é:m = n/2 = (1/2) m(AB)
Ângulo reto inscrito na circunferência
O arco correspondente a um ângulo reto inscrito em uma circunferência é a semi-circunferência. Se um triângulo inscrito numa semi-circunferência tem um lado igual ao diâmetro, então ele é um triângulo retângulo e esse diâmetro é a hipotenusa do triângulo.
Ângulo semi-inscrito e arco capaz
Ângulo semi-inscrito: Ângulo semi-inscrito ou ângulo de segmento é um ângulo que possui um dos lados tangente à circunferência, o outro lado secante à circunferência e o vértice na circunferência. Este ângulo determina um arco (menor) sobre a circunferência. No gráfico ao lado, a reta secante passa pelos pontos A e B e o arco correspondente ao ângulo semi-inscrito BAC é o arco AXB onde X é um ponto sobre o arco.

Observação
A medida do ângulo semi-inscrito é a metade da medida do arco interceptado. Na figura, a medida do ângulo BÂC é igual a metade da medida do arco AXB.Arco capaz
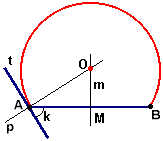
Dado um segmento AB e um ângulo k, pergunta-se: Qual é o lugar geométrico de todos os pontos do plano que contém os vértices dos ângulos cujos lados passam pelos pontos A e B sendo todos os ângulos congruentes ao ângulo k? Este lugar geométrico é um arco de circunferência denominado arco capaz.
Construção do arco capaz com régua e compasso:
Traçar um segmento de reta AB;Pelo ponto A, trace uma reta t formando com o segmento AB um ângulo congruente a k (mesma medida que o ângulo k);
Traçar uma reta p perpendicular à reta t passando pelo ponto A;
Determinar o ponto médio M do segmento AB;
Traçar a reta mediatriz m ao segmento AB;
Obter o ponto O que é a interseção entre a reta p e a mediatriz m.
Com o compasso centrado no ponto O e abertura OA, traçar o arco de circunferência localizado acima do segmento AB.
O arco que aparece em vermelho no gráfico ao lado é o arco capaz.
Observação: Todo ângulo inscrito no arco capaz AB, com lados passando pelos pontos A e B são congruentes e isto significa que, o segmento de reta AB é sempre visto sob o mesmo ângulo de visão se o vértice deste ângulo está localizado no arco capaz. Na figura abaixo à esquerda, os ângulos que passam por A e B e têm vértices em V1, V2, V3, ..., são todos congruentes (a mesma medida).


m(arco AB) = 2 medida(m) = medida(n)
Outras propriedades com cordas e segmentos
Agora apresentaremos alguns resultados que fazem a conexão entre segmentos e cordas, que não são evidentes à primeira vista. Se a reta AB é tangente à circunferência no ponto B então o segmento AB é o segmento tangente de A até a circunferência. Se a reta RT é uma reta secante que intercepta a circunferência em S e T e R é um ponto exterior a circunferência, então RT é um segmento secante e RS é a parte externa do segmento secante.
Cordas interceptando dentro da circunferência: Se duas cordas de uma mesma circunferência se interceptam em um ponto P dentro da circunferência, então o produto das medidas das duas partes de uma corda é igual ao produto das medidas das duas partes da outra corda.

(AP).(PB) = (CP).(PD)
Potência de ponto (1)
A partir de um ponto fixo P dentro de uma circunferência, tem-se que (PA).(PB) é constante qualquer que seja a corda AB passando por este ponto P. Este produto (PA).(PB) é denominado a potência do ponto P em relação a esta circunferência.Secantes interceptando fora da circunferência
Consideremos duas retas secantes a uma mesma circunferência que se interceptam em um ponto P localizado fora da circunferência.Se uma das retas passa pelos pontos A e B e a outra reta passa pelos pontos C e D da circunferência, então o produto da medida do segmento secante PA pela medida da sua parte exterior PB é igual ao produto da medida do segmento secante PC pela medida da sua parte exterior PD.

(PA).(PB)=(PC).(PD)
Potência de ponto (2)
Se P é um ponto fixo fora da circunferência, o produto (PA).(PB) é constante qualquer que seja a reta secante à circunferência passando por P. Este produto (PA).(PB) é também denominado a potência do ponto P em relação à circunferência.Secante e tangente interceptando fora da circunferência
Se uma reta secante e uma reta tangente a uma mesma circunferência se interceptam em um ponto P fora da circunferência, a reta secante passando pelos pontos A e B e a reta tangente passando pelo ponto T de tangência à circunferência, então o quadrado da medida do segmento tangente PT é igual ao produto da medida do segmento secante PA pela medida da sua parte exterior PB.
(PT)2 = (PA).(PB)
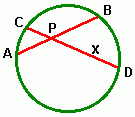
Exemplo: Consideremos a figura ao lado com as cordas AB e CD tendo interseção no ponto P, com (AP) = 5cm, (PB) = 8cm, (CD) = 14cm. Iremos obter a medida do segmento PD. Tomaremos (PD)=x, para podermos escrever que (CP) = 14-x e somente utilizaremos a unidade de medida no final.Desse modo, (PD).(PC)=(PA).(PB) e podemos escrever que x(14-x)=5×8, de onde segue que x²-14x+40=0. Resolvendo esta equação do segundo grau, obtemos: x=4 ou x=10, o que significa que se uma das partes do segmento medir 4cm, a outra medirá 10cm. Pela figura anexada, observamos que o segmento PD é maior que o segmento PC e concluímos que (PD)=10cm e (PC)=4cm.

Fonte: pessoal.sercomtel.com.br
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferência
CircunferênciaMarcos Noé Circunferência e seus elementosNo cotidiano identificamos objetos e construções que lembram uma circunferência, um contorno ou regiões circulares. A circunferência possui propriedades e definições...
- Posição Relativa Entre Uma Reta E Uma Circunferência
Posição relativa entre uma reta e uma circunferênciaMarcelo Rigonatto CircunferênciaConsidere uma circunferência no plano de cento O(xo, yo) e raio r. Dada uma reta s de equação ax + by +c = 0, também do mesmo plano. A reta...
- Circunferência
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br A importância da circunferênciaA...
- Construções Geométricas De Tangentes Com Régua E Compasso (parte 2)
Nesta segunda parte sobre construção de tangentes, vamos resolver três problemas clássicos sobre traçados de tangentes utilizando régua e compasso. 1) São dados dois pontos O e P e uma distância d. Conduzir uma reta por P que diste d de O. [Figura...