Matemática
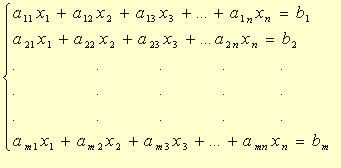
Vamos abordar a classificação de um sistema de duas equações do 1º grau com duas incógnitas. Ao resolver os sistemas pelo método da adição ou da substituição, verificaremos três condições de classificação:
Sistema Determinado – SD
Sistema Possível Indeterminado – SID
Sistema Impossível – SI
Sistema Determinado
Um sistema de equações é considerado determinado quando apresenta uma única solução, isto é, no caso de um sistema de duas equações do 1º grau com duas incógnitas, há um único par ordenado. Observe:
Ao resolvermos o sistema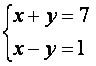
, obtemos uma única possível solução: (4, 3).
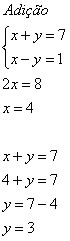
Sistema Possível Indeterminado
Esse sistema admite infinitas soluções, isto é, temos infinitos pares ordenados (x, y) que satisfazem ao sistema. Observe o sistema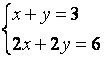
, ele possui infinitas soluções.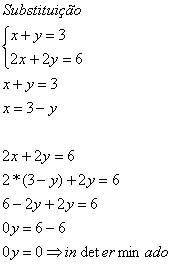
Observe que quando temos 0y = 0, podemos considerar qualquer valor para y que mesmo assim, a igualdade se mantém verdadeira.
Sistema Impossível
Nesse sistema dizemos que não existem soluções possíveis, isto é, ele não possui par ordenado que satisfaça à condição do sistema de equações. Na resolução do sistema ocorre uma condição inexistente na Matemática. Observe: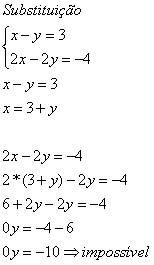
- Sistema De Equação
Gráfico de uma equação de 1º grau com duas variáveis Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções. Cada uma dessas soluções pode ser representada por um par ordenado (x, y). Dispondo de dois pares ordenados...
- Sistema De Duas Equações
Um sistema de equações do 1º grau com duas incógnitas é formado por duas equações, onde cada equação possui duas variáveis x e y. Veja o exemplo: A resolução de um sistema consiste em calcular o valor de x e y que satisfazem as equações...
- Sistema Linear Homogêneo
Um sistema linear é homogêneo quando os coeficientes, independente de todas as suas equações lineares, são iguais a zero. Esse tipo de sistema possui pelo menos uma solução possível, pois podemos obter como resultado o terno (0, 0, 0), chamamos...
- Sistemas
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Sistemas Lineares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
Matemática
Classificação de um Sistema de Equações:
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso www.accbarrosogestar.wordpress.com
email [email protected]
Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com
Classificação de um Sistema de Equações:
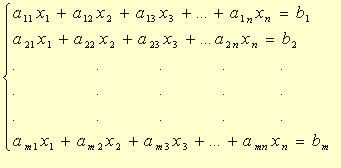
Sistemas
Sistema Determinado – SD
Sistema Possível Indeterminado – SID
Sistema Impossível – SI
Sistema Determinado
Um sistema de equações é considerado determinado quando apresenta uma única solução, isto é, no caso de um sistema de duas equações do 1º grau com duas incógnitas, há um único par ordenado. Observe:
Ao resolvermos o sistema
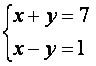, obtemos uma única possível solução: (4, 3).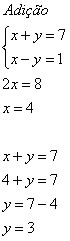Sistema Possível Indeterminado
Esse sistema admite infinitas soluções, isto é, temos infinitos pares ordenados (x, y) que satisfazem ao sistema. Observe o sistema
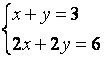, ele possui infinitas soluções.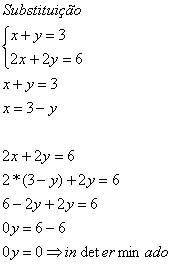Observe que quando temos 0y = 0, podemos considerar qualquer valor para y que mesmo assim, a igualdade se mantém verdadeira.
Sistema Impossível
Nesse sistema dizemos que não existem soluções possíveis, isto é, ele não possui par ordenado que satisfaça à condição do sistema de equações. Na resolução do sistema ocorre uma condição inexistente na Matemática. Observe:
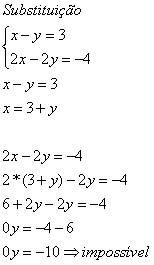
- Sistema De Equação
Gráfico de uma equação de 1º grau com duas variáveis Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções. Cada uma dessas soluções pode ser representada por um par ordenado (x, y). Dispondo de dois pares ordenados...
- Sistema De Duas Equações
Um sistema de equações do 1º grau com duas incógnitas é formado por duas equações, onde cada equação possui duas variáveis x e y. Veja o exemplo: A resolução de um sistema consiste em calcular o valor de x e y que satisfazem as equações...
- Sistema Linear Homogêneo
Um sistema linear é homogêneo quando os coeficientes, independente de todas as suas equações lineares, são iguais a zero. Esse tipo de sistema possui pelo menos uma solução possível, pois podemos obter como resultado o terno (0, 0, 0), chamamos...
- Sistemas
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Sistemas Lineares
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...