Matemática
Chamamos de sistema linear um conjunto de equações lineares. Esse conjunto pode ter m equações e n incógnitas. Resolver um sistema linear consiste em determinar o conjunto solução de suas incógnitas, isto é, encontrar os valores desconhecidos que tornem o sistema verdadeiro.
De acordo com a solução, um sistema pode ser classificado da seguinte forma:
Possível e determinado: uma única solução
Possível e indeterminado: infinitas soluções
Impossível: não possui soluções.
Observe o seguinte sistema linear com três equações e três incógnitas:
Exemplo 1
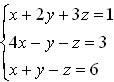
Devemos aplicar conhecimentos matemáticos relacionados à resolução de sistemas no intuito de descobrir os valores de x, y e z. Nessas situações, o cálculo mental se torna muito complexo. Observe o método de resolução oferecido para este sistema linear:
1ª equação – Isolar x
x + 2y + 3z = 1
x = 1 – 2y – 3z
2ª equação – Substituir x por 1 – 2y – 3z
4x – y – z = 3
4 * (1 – 2y – 3z) – y – z = 3
4 – 8y – 12z – y – z = 3
–9y – 13z = 3 – 4
–9y – 13z = – 1
3ª equação – Substituir x por 1 – 2y – 3z
x + y – z = 6
1 – 2y – 3z + y – z = 6
– y – 4z = 6 – 1
– y – 4z = 5
Resolver o novo sistema determinando os valores de z e y.
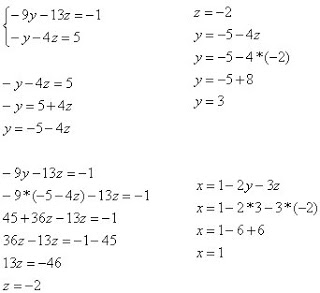
A solução do sistema linear é: x = 1, y = 3 e z = –2. Nesse caso, o sistema é possível e determinado.
Exemplo 2
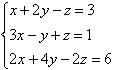
Isolar x na 1ª equação
x + 2y – z = 3
x = 3 – 2y + z
Substituir x na 2ª equação
3x – y + z = 1
3 * (3 – 2y + z) – y + z = 1
9 – 6y + 3z – y + z = 1
– 7y + 4z = – 8
Substituir x na 3ª equação
2x + 4y – 2z = 6
2 * (3 – 2y + z) + 4y – 2z = 6
6 – 4y + 2z + 4y – 2z = 6
0y + 0z = 6 – 6
0y + 0z = 0
Na ocorrência dessa situação dizemos que o sistema é possível e indeterminado, pois nesse caso as incógnitas admitem infinitas soluções. Por qualquer valor que trocarmos y e z na equação 0y + 0z = 0, tornamos a sentença verdadeira. Observe:
y = 3 e z = 4
0 * 3 + 0 * 4 = 0 → verdadeiro
y = 7 e z = – 4
0 * 7 + 0 * (–4) = 0 → verdadeiro
Um sistema será impossível quando na sua resolução ocorrer sentença semelhante a 0y = 4, pois nessas condições temos uma divisão impossível, 4 / 0.
www.bancodeconcursos.com
- Sistema Linear Homogêneo
Um sistema linear é homogêneo quando os coeficientes, independente de todas as suas equações lineares, são iguais a zero. Esse tipo de sistema possui pelo menos uma solução possível, pois podemos obter como resultado o terno (0, 0, 0), chamamos...
- Sistemas E Equações Lineares
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Sistemas
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Classificação De Um Sistema De Equações:
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso www.accbarrosogestar.wordpress.com email [email protected] HTTP://ensinodematemtica.blogspot.com...
- Sistema De Equações Do 1º Grau
Colégio Estadual Dinah gonçalves http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com Professor antonio carlos c Barroso apostila sobre sistema de 1º grau para 7ª série ou 8ª ano Para encontrarmos numa equação...
Matemática
Sistemas Lineares
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
WWW.profantoniocarneiro.com
Chamamos de sistema linear um conjunto de equações lineares. Esse conjunto pode ter m equações e n incógnitas. Resolver um sistema linear consiste em determinar o conjunto solução de suas incógnitas, isto é, encontrar os valores desconhecidos que tornem o sistema verdadeiro.
De acordo com a solução, um sistema pode ser classificado da seguinte forma:
Possível e determinado: uma única solução
Possível e indeterminado: infinitas soluções
Impossível: não possui soluções.
Observe o seguinte sistema linear com três equações e três incógnitas:
Exemplo 1
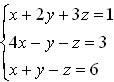
Devemos aplicar conhecimentos matemáticos relacionados à resolução de sistemas no intuito de descobrir os valores de x, y e z. Nessas situações, o cálculo mental se torna muito complexo. Observe o método de resolução oferecido para este sistema linear:
1ª equação – Isolar x
x + 2y + 3z = 1
x = 1 – 2y – 3z
2ª equação – Substituir x por 1 – 2y – 3z
4x – y – z = 3
4 * (1 – 2y – 3z) – y – z = 3
4 – 8y – 12z – y – z = 3
–9y – 13z = 3 – 4
–9y – 13z = – 1
3ª equação – Substituir x por 1 – 2y – 3z
x + y – z = 6
1 – 2y – 3z + y – z = 6
– y – 4z = 6 – 1
– y – 4z = 5
Resolver o novo sistema determinando os valores de z e y.
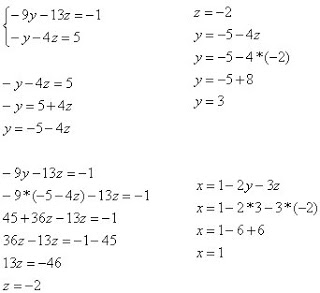
A solução do sistema linear é: x = 1, y = 3 e z = –2. Nesse caso, o sistema é possível e determinado.
Exemplo 2
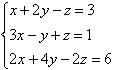
Isolar x na 1ª equação
x + 2y – z = 3
x = 3 – 2y + z
Substituir x na 2ª equação
3x – y + z = 1
3 * (3 – 2y + z) – y + z = 1
9 – 6y + 3z – y + z = 1
– 7y + 4z = – 8
Substituir x na 3ª equação
2x + 4y – 2z = 6
2 * (3 – 2y + z) + 4y – 2z = 6
6 – 4y + 2z + 4y – 2z = 6
0y + 0z = 6 – 6
0y + 0z = 0
Na ocorrência dessa situação dizemos que o sistema é possível e indeterminado, pois nesse caso as incógnitas admitem infinitas soluções. Por qualquer valor que trocarmos y e z na equação 0y + 0z = 0, tornamos a sentença verdadeira. Observe:
y = 3 e z = 4
0 * 3 + 0 * 4 = 0 → verdadeiro
y = 7 e z = – 4
0 * 7 + 0 * (–4) = 0 → verdadeiro
Um sistema será impossível quando na sua resolução ocorrer sentença semelhante a 0y = 4, pois nessas condições temos uma divisão impossível, 4 / 0.
www.bancodeconcursos.com
- Sistema Linear Homogêneo
Um sistema linear é homogêneo quando os coeficientes, independente de todas as suas equações lineares, são iguais a zero. Esse tipo de sistema possui pelo menos uma solução possível, pois podemos obter como resultado o terno (0, 0, 0), chamamos...
- Sistemas E Equações Lineares
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Sistemas
Equações Lineares As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente. A equação 4x – 3y + 5z = 31 é uma equação...
- Classificação De Um Sistema De Equações:
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso www.accbarrosogestar.wordpress.com email [email protected] HTTP://ensinodematemtica.blogspot.com...
- Sistema De Equações Do 1º Grau
Colégio Estadual Dinah gonçalves http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com Professor antonio carlos c Barroso apostila sobre sistema de 1º grau para 7ª série ou 8ª ano Para encontrarmos numa equação...
