Matemática

Comunicando-se por Computador em Linguagem Matemática

Introdução

A Matemática é uma ciência que possui seus próprios métodos. Mais do que isso, a Matemática possui uma linguagem própria, repleta de símbolos e notações especiais. Por exemplo, em álgebra elementar aprendemos que

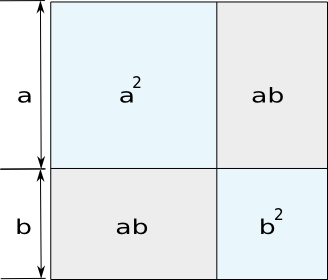
(a + b) 2 = a 2 + 2 a b + b 2 .

Vocês já pensaram como seria comunicar essa identidade algébrica sem auxílio da notação matemática que conhecemos? Antigamente, quando a notação matemática não havia se consolidado ainda, a identidade acima poderia ser comunicada com palavras, mais ou menos desta forma: "O quadrado da soma de dois números é igual a soma de seus quadrados mais duas vezes o produto do primeiro pelo segundo". Ou ainda com auxílio de uma figura como esta:

Enquanto essas maneiras alternativas de expressar a identidade tenham seu valor, é inegável que a primeira forma é muito mais precisa e econômica. Essa é a principal razão porque foi necessário desenvolver uma linguagem apropriada para a Matemática.

A notação tradicional é muito conveniente para ser escrita à mão, pois é assim que a Matemática ainda é comunicada em quadros e cadernos. Mas como escrever essas fórmulas complicadas usando o computador? Existem várias maneiras, mas a mais utilizada por matemáticos profissionais é o sistema TEX de composição (a pronúncia é "téqui").

O TEX foi desenvolvido pelo matemático e cientista da computação Donald Knuth com o propósito de facilitar a composição de textos científicos em computador. É o sistema mais usado hoje em dia nas áreas de Física e Matemática, sendo utilizado também em outras ciências. Trata-se de um sistema muito complexo, mas nós vamos nos concentrar só na parte de composição de fórmulas matemáticas do TEX. As fórmulas do TEX podem ser utilizadas em blogs e fóruns da internet, no gmail e no aplicativo GeoGebra. Podemos também testar as fórmulas interativamente no editor de equações.

Fórmulas em `TEX`

A ideia básica do TEX é utilizar somente os caracteres presentes em um teclado para representar todos os símbolos e convenções da Matemática. É claro que existem mais símbolos matemáticos do que caracteres em um teclado, assim alguns símbolos precisarão de mais de um caractere. Além disso, é necessário alguma marcação para indicar onde uma fórmula matemática se inicia e onde ela termina. Em geral, utilizamos cifrões para delimitar as fórmulas, na forma $ fórmula $, mas dependendo do sistema os delimitadores são implícitos.

Para ver como o TEX funciona, experimente digitar 2+2=4 no editor de equações. Vôce vai obter algo como

2 + 2 = 4

Note como os algarismos aparecem diferentes e como os símbolos para adição e igualdade estão maiores e mais bonitos. Perceba ainda o espaçamento entre os algarismos e os símbolos. Não foi necessário dizer nada sobre o espaçamento, o próprio TEX encontrou o ajuste que deixa a fórmula mais agradável de ser lida. Essa é a nossa primeira lição doTEX : o próprio TEX determina os espaçamentos adequados, portanto espaços não são necessários.

Fórmulas simples que envolvam apenas multiplicação, adição, subtração e igualdade de variáveis e algarismos são representadas em TEX da mesma forma que a usual. Ilustramos alguns exemplos na tabela abaixo, onde a primeira coluna contém a representação da fórmula em TEX e a segunda o resultado final. Experimente digitar algumas dessas fórmulas no editor de equações.

TEX	Resultado
x+2=3	x+2=3
a(b-c)=ab-ac	a(b−c)=ab−ac
ab=ba	ab=ba
a(bc)=(ab)c=abc	a(bc)=(ab)c=abc

Superescrito e Subscrito

Uma notação matemática muito comum é o superescrito, quando colocamos um símbolo ou expressão à direita e acima de uma outra expressão. O superescrito ocorre por exemplo na operação de exponenciação. Para representar o produto de um número a por si mesmo colocamos um 2 acima e à direita do a :

a \times a = a 2

Nesse caso dizemos que o 2 está superescrito ao a . No TEX , a notação de superescrito é obtida com o caractere ^ (circumflexo), que dá uma ideia de "acima". Veja na tabela abaixo alguns exemplos de superescrito.

TEX	Resultado
x^2+1=0	x2+1=0
(a+b)^2=a^2+2ab+b^2	(a+b)2=a2+2ab+b2
99^2=(100-1)^2=100^2-200+1=99801	992=(100−1)2=1002−200+1=99801

O subescrito é similar ao superescrito, só que agora o símbolo ou expressão em subescrito fica à direita e abaixo. Subescritos são muito usados para enumerações e índices. No TEXo subescrito é obtido com o caractere _ (sublinha), que dá uma ideia de "abaixo". Acompanhe os exemplos a seguir.

TEX	Resultado
a_1+a_2+a_3=0	a1+a2+a3=0
a_i-b_j=c_k	ai−bj=ck

Agrupamento e Macros

Às vezes uma expressão pode ser ambígua, ou seja, pode ter mais de uma interpretação. Por exemplo, se escrevemos 2^x-1, queremos dizer 2x−1 ou 2x−1 ? Para resolver problemas como esse, o TEX emprega a técnica de agrupamento que consiste em cercar uma expressão com chaves { } para que ela se comporte como um único caractere. Veja os exemplos abaixo.

TEX	Resultado
x^{10}+1=0	x10+1=0
2^{a+b}=2^a 2^b	2a+b=2a2b
a_{ij}=a_{ji}	aij=aji

Experimente digitar os exemplos acima no editor de equações sem as chaves para ver o que acontece.

Note que as chaves não aparecem, elas apenas servem para demarcar um grupo de símbolos. Mas como fazer para exibir as chaves? É como falamos antes, como o número de caracteres em um teclado é menor que o número de símbolos matemáticos, alguns símbolos devem ser representados por mais de um caractere. Para representar as chaves, por exemplo, usamos \{ e \}:

TEX	Resultado
A=\{1,2,3\}	A={1,2,3}
\{a+2[b+3(c+d)]\}	{a+2[b+3(c+d)]}

Outros símbolos são representados colocando-se uma barra invertida \ antes do nome em inglês do símbolo. Por exemplo, listamos na tabela abaixo a representação em TEX de algumas letras gregas mais frequentes:

\TeX	Resultado
\alpha	α
\beta	β
\gamma	γ
\delta	δ
\epsilon	ϵ
\phi	ϕ
\pi	π
\theta	θ
\omega	ω

De maneira geral, essas palavras precedidas de barra invertida são chamadas de macros. Macros possuem mil e uma utilidades que com o tempo vocês irão aprender. Por enquanto vamos listar algumas macros usadas para representar símbolos mais conhecidos.

TEX	Resultado	Significado
\times	×	vezes
\div	÷	dividido
\leq	≤	menor ou igual
\geq	≥	maior ou igual
\in	∈	pertence
\subset	⊂	está contido
\cup	∪	união
\cap	∩	interseção
\exists	∃	existe
\forall	∀	para todo
\Rightarrow	⇒	implica
\Leftrightarrow	⇔	é equivalente a
\cdots	⋯	reticências

Não se preocupem em decorar todas essas macros. Vocês vão naturalmente fixar o nome delas na medida em que for necessário. Vejam alguns exemplos onde as macros se misturam:

TEX	Resultado
\alpha+\beta+\gamma=\pi	α+β+γ=π
A\cap(B\cup C)=(A\cap B)\cup(A\cap C)	A∩(B∪C)=(A∩B)∪(A∩C)
A=a_1+a_2+\cdots+a_n	A=a1+a2+⋯+an
(x-1)^2\geq 0	(x+1)2≥0
a\leq 0 \Leftrightarrow -a\geq 0	a≤0⇔−a≥0

Frações e Raízes

Macros também são úteis em construções mais complexas. Por exemplo, para representar uma fração, colocamos o numerador e o denominador separados por uma barra. Usamos a macro \frac{numerador}{denominador} para obter este resultado.

TEX	Resultado
\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}	$a b + c d = a d + b c b d$
f(x)=2^{\frac{1}{x}}	$f (x) = 2 1 x$

Raízes também são notações complexas, pois uma barra horizontal deve cobrir todo o radicando. A raiz quadrada de uma expressão R tem a forma \sqrt{R}. Se quisermos a raiz n-ésima, a macro tem a forma \sqrt[n]{R}. Confira os exemplos abaixo.

TEX	Resultado
f(x)=\frac{1}{\sqrt{x}}	$f (x) = 1 x - \sqrt$
g(x)=\sqrt[3]{x^2-1}	$g (x) = x 2 - 1 - - - - - - \sqrt 3$

Conclusão

O TEX é um sistema muito poderoso de composição de textos, com muitos recursos além dos vistos acima. Mas essas construções básicas são suficientes para a maioria das fórmulas encontradas no ensino médio.

http://www.dmat.ufba.br/~vinicius.mello

- Equação Do Segundo Grau - Parte Ii - Fórmula De Bhaskara E Outros
Olá, gente. Há um tempo eu postei algo sobre equações do segundo grau (clique aqui para ver).Analisaremos o caso em que temos , onde x é a incógnita, e . Para este caso, há 3 formas principais de resolver tal equação, são elas: I- Completar...

- O Problema Dos Quatro Quatros
O objetivo do problema dos quatro quatros é formar números inteiros usando quatro algarismos 4 e operações aritméticas elementares. Por exemplo, para formar...

- LÓgica MatemÁtica
CÁLCULO PROPOSICIONAL Como primeira e indispensável parte da Lógica Matemática temos o CÁLCULO PROPOSICIONAL ou CÁLCULO SENTENCIAL ou ainda CÁLCULO DAS SENTENÇAS. CONCEITO DE PROPOSIÇÃO PROPOSIÇÃO: sentenças...

- NoÇÕes De LÓgica MatemÁtica
CÁLCULO PROPOSICIONAL Como primeira e indispensável parte da Lógica Matemática temos o CÁLCULO PROPOSICIONAL ou CÁLCULO SENTENCIAL ou ainda CÁLCULO DAS SENTENÇAS. CONCEITO DE PROPOSIÇÃO PROPOSIÇÃO: sentenças...

- Algumas Observações Sobre A Notação De Derivada
No Cálculo, notações diferentes para a derivada é um fato e cada uma delas é de uso comum e as utilizamos conforme as circunstâncias em que os símbolos estão sendo usados. Então o que nos importa quais símbolos utilizamos se todos servem para...

Matemática