Matemática
Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...}
É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá como resultado um número natural, já a subtração entre dois números naturais nem sempre é um número natural, como por exemplo 2 - 5, não pertence aos N, temos então o surgimento do conjunto dos números inteiros.
No conjunto dos inteiros destacamos os seguintes subconjuntos:
Z* = Z - {0} = {...-3,-2,-1,1,2,3...}
Z+ = {0,1,2,3,4...} (inteiros não negativos)
Z - = {0,-1,-2,-3,-4...} (inteiros não positivos)
Z*+ = {1,2,3,4...} (inteiros positivos)
Z*- = {-1,-2,-3,-4...} (inteiros não negativos)
Neste conjunto sempre é possível efetuar a adição, a multiplicação e a subtração entre números inteiros, isto é, sempre estas operações resultam em um número inteiro. Já a divisão nem sempre resulta em um número inteiro, como por exemplo, 7 : 2 ,não pertence aos inteiros surgindo assim o conjunto dos racionais.
O conjunto dos números racionais Q é a união do conjunto dos números naturais (N), inteiros (Z) e as frações positivas e negativas, como por exemplo:
Q = -5 ; - 4/3 ; - 1; 0; 0,25 ; 1/2 ; 3/4 ; 1; 6/5 ; 2
Obs: Um número racional pode aparecer em forma de dízima periódica, isto é, um numeral decimal, com a parte decimal formada por infinitos algarismos que se repetem periodicamente, como por exemplo: 4,5555 (período 5) , 10,878787 (período 87) e 9,8545454... (período 54, parte não periódica 8)
Exemplo: transformar em frações irredutíveis os números:
a) 0,1111....
x=0,111...
10x=1,111...
daí,
10x-x=1
x=1/9
portanto, 0,111...=1/9
b) 2,1343434...
x=2,1343434...
10x=21,3434...
1000x=2134,3434....
daí,
1000x-10x=2113
x=2113/990
portanto, 2,1343434...=2113/990
- raiz quadrada de três = 1,73...;
- dízimas não periódicas;
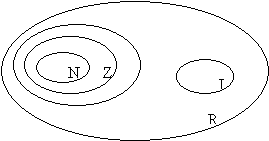
- Conjuntos Numéricos
Os números são indispensáveis no estudo da Matemática e, por isso, são organizados em conjuntos que possuem características próprias. Ao longo da evolução da Matemática, os números foram surgindo e sendo classificados como Naturais, Inteiros,...
- Conjuntos
Lucas Martins Conjunto dos Números Naturais São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N. Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar...
- Conjuntos
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comAlguns...
- Conjuntos Numéricos
Conjunto dos Números Naturais (IN) Um subconjunto importante de IN é o conjunto IN*: IN*={1, 2, 3, 4, 5,...} ► o zero foi excluído do conjunto IN. Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico...
- Conjunto Númerico
Conjuntos Numéricos I) Números Naturais N = { 0 , 1 , 2 , 3 , ... } II) Números Inteiros Z = { ... , -2 , -1 , 0 , 1 , 2, ... } Todo número natural é inteiro, isto é, N é um subconjunto de Z III) Números Racionais - São aqueles que podem...
Matemática
Conjuntos Numéricos
1- Naturais (IN)
N = {0,1,2,3,4,5...}Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...}
É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá como resultado um número natural, já a subtração entre dois números naturais nem sempre é um número natural, como por exemplo 2 - 5, não pertence aos N, temos então o surgimento do conjunto dos números inteiros.
2- Inteiros (Z)
Z = {...-3,-2,-1,0,1,2,3...}No conjunto dos inteiros destacamos os seguintes subconjuntos:
Z* = Z - {0} = {...-3,-2,-1,1,2,3...}
Z+ = {0,1,2,3,4...} (inteiros não negativos)
Z - = {0,-1,-2,-3,-4...} (inteiros não positivos)
Z*+ = {1,2,3,4...} (inteiros positivos)
Z*- = {-1,-2,-3,-4...} (inteiros não negativos)
Neste conjunto sempre é possível efetuar a adição, a multiplicação e a subtração entre números inteiros, isto é, sempre estas operações resultam em um número inteiro. Já a divisão nem sempre resulta em um número inteiro, como por exemplo, 7 : 2 ,não pertence aos inteiros surgindo assim o conjunto dos racionais.
3-Racionais (Q)
Q = {x tal que x = a/b (a sobre b) onde aÎ (pertence) Z a b E Z* (Z menos o zero)}.O conjunto dos números racionais Q é a união do conjunto dos números naturais (N), inteiros (Z) e as frações positivas e negativas, como por exemplo:
Q = -5 ; - 4/3 ; - 1; 0; 0,25 ; 1/2 ; 3/4 ; 1; 6/5 ; 2
Obs: Um número racional pode aparecer em forma de dízima periódica, isto é, um numeral decimal, com a parte decimal formada por infinitos algarismos que se repetem periodicamente, como por exemplo: 4,5555 (período 5) , 10,878787 (período 87) e 9,8545454... (período 54, parte não periódica 8)
Exemplo: transformar em frações irredutíveis os números:
a) 0,1111....
x=0,111...
10x=1,111...
daí,
10x-x=1
x=1/9
portanto, 0,111...=1/9
b) 2,1343434...
x=2,1343434...
10x=21,3434...
1000x=2134,3434....
daí,
1000x-10x=2113
x=2113/990
portanto, 2,1343434...=2113/990
4-Irracionais (I) - É todo número decimal não-exato e não periódico, bem como toda raiz não-exata.
- raiz quadrada de dois = 1,414...;- raiz quadrada de três = 1,73...;
- dízimas não periódicas;
5-Reais (IR)

Fonte: www.ficharionline.com
- Conjuntos Numéricos
Os números são indispensáveis no estudo da Matemática e, por isso, são organizados em conjuntos que possuem características próprias. Ao longo da evolução da Matemática, os números foram surgindo e sendo classificados como Naturais, Inteiros,...
- Conjuntos
Lucas Martins Conjunto dos Números Naturais São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N. Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar...
- Conjuntos
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comAlguns...
- Conjuntos Numéricos
Conjunto dos Números Naturais (IN) Um subconjunto importante de IN é o conjunto IN*: IN*={1, 2, 3, 4, 5,...} ► o zero foi excluído do conjunto IN. Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico...
- Conjunto Númerico
Conjuntos Numéricos I) Números Naturais N = { 0 , 1 , 2 , 3 , ... } II) Números Inteiros Z = { ... , -2 , -1 , 0 , 1 , 2, ... } Todo número natural é inteiro, isto é, N é um subconjunto de Z III) Números Racionais - São aqueles que podem...
