Matemática
O conjunto de todos os números naturais.
O conjunto dos números reais tal que x2-4=0.
Em geral, um conjunto é denotado por uma letra maiúscula do alfabeto: A, B, C, ..., Z.
1 é um elemento do conjunto dos números naturais.
-2 é um elemento do conjunto dos números reais que satisfaz à equação x2-4=0.
Em geral, um elemento de um conjunto, é denotado por uma letra minúscula do alfabeto: a, b, c, ..., z.
1 pertence ao conjunto dos números naturais.
-2 pertence ao conjunto de números reais que satisfaz à equação x2-4=0.
Se um elemento pertence a um conjunto utilizamos o símbolo
, que se lê: "pertence".
N
Para afirmar que 0 não é um número natural, escrevemos:
0N
Um símbolo matemático para a negação é a barra /.
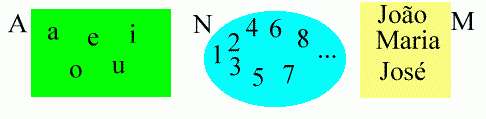
Apresentação: Os elementos do conjunto estão dentro de duas chaves { e }.
A = { a, e, i, o, u }
N = { 1, 2, 3, 4, ... }
M = { João, Maria, José }
Descrição: O conjunto é descrito por uma ou mais propriedades.
A = { x : x é uma vogal}
N = { x : x é um número natural}
M = { x : x é uma pessoa da família de Maria}
Diagrama de Venn-Euler (lê-se: "Ven-óiler"): Os conjuntos são mostrados graficamente
B, se todos os elementos de A também estão em B. Algumas vezes diremos que um conjunto A está propriamente contido em B, quando o conjunto B, além de conter os elementos de A, contém também outros elementos. O conjunto A é denominado subconjunto de B e o conjunto B é o superconjunto que contém A.
Conjunto universo: É um conjunto que contém todos os elementos do contexto no qual estamos trabalhando e também contém todos os conjuntos desse contexto. O conjunto universo é representado por uma letra U. Na sequência não mais usaremos o conjunto universo.
AB = { x: aA ou xB }
A
B = { x: aA e xB }
Quando a interseção de dois conjuntos A e B é o conjunto vazio, dizemos que estes conjuntos são disjuntos.
B e a interseção de A e B, denotada por AB, ainda são conjuntos no universo.
Reflexiva: Qualquer que seja o conjunto A, tem-se que:
AA = A e A A = A
1. Inclusão: Quaisquer que sejam os conjuntos A e B, tem-se que:
AAB, BAB, ABA, ABB
2. Inclusão relacionada: Quaisquer que sejam os conjuntos A e B, tem-se que:
AB equivale a AB = B
AB equivale a AB = A
3. Associativa: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A(BC) = (AB)C
A(BC) = (AB)C
4. Comutativa: Quaisquer que sejam os conjuntos A e B, tem-se que:
AB = BA
AB = BA
5. Elemento neutro para a reunião: O conjunto vazio Ø é o elemento neutro para a reunião de conjuntos, tal que para todo conjunto A, se tem:
AØ = A
6. Elemento "nulo" para a interseção: A interseção do conjunto vazio Ø com qualquer outro conjunto A, fornece o próprio conjunto vazio.
AØ = Ø
7. Elemento neutro para a interseção: O conjunto universo U é o elemento neutro para a interseção de conjuntos, tal que para todo conjunto A, se tem:
AU = A
8. Distributiva: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A( B C ) = ( A B ) ( A C )
A ( B C ) = ( A B ) (A C )
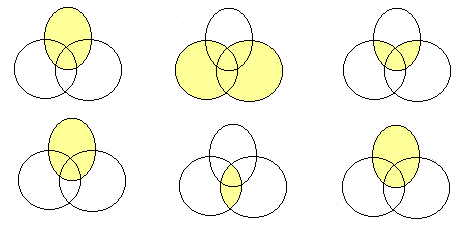
Os gráficos abaixo mostram a distributividade.
A-B = { x: a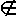
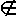e x B
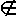C BA = A-B = { x: x A e x B }
Quando não existe dúvida sobre o universo U em que trabalhamos, simplesmente utilizamos a letra c posta como um expoente no conjunto, para indicar o complemento deste conjunto. Exemplos especiais são: Øc=U e Uc=Ø.
(AB)c = Ac Bc
O complementar da reunião de uma coleção finita de conjuntos é a interseção dos complementares desses conjuntos.
(A1 A2 ... An)c = A1c A2c ... Anc
O complementar da interseção de dois conjuntos é a reunião dos complementares desses conjuntos.
(AB)c = Ac Bc
AB = { x: xAB e xAB }
A situação gráfica para a diferença simétrica é:
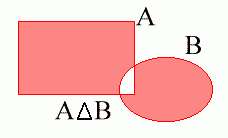Exercício: Dados os conjuntos A, B e C, mostrar que:
1. A=Ø se, e somente se, B=A
B.
2. O conjunto vazio é o elemento neutro para a operação de diferença simétrica. Usar o ítem anterior.
3. A diferença simétrica é comutativa.
4. A diferença simétrica é associativa.
5. AA=Ø (conjunto vazio).
6. A interseção entre A e BC é distributiva, isto é:
A(BC) = (AB)(AC)
7. AB está contida na reunião de AC e de BC, mas esta inclusão é própria, isto é:
AB (AC)(BC)
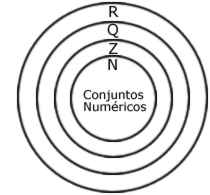
conjuntos numéricos
I) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
II) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
I) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
II) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
III) Números Racionais
- São aqueles que podem ser expressos na forma a/b, onde a e b são inteiros quaisquer, com b diferente de 0.
Assim como exemplo podemos citar o -1/2 , 1 , 2,5 ,...
-Números decimais exatos são racionais
Pois 0,1 = 1/10
2,3 = 23/10 ...
- Números decimais periódicos são racionais.
0,1111... = 1/9
0,3232 ...= 32/99
2,3333 ...= 21/9
0,2111 ...= 19/90
-Toda dízima periódica 0,9999 ... 9 ... é uma outra representação do número 1.
-São compostos por dízimas infinitas não periódicas.
Intervalo fechado nos extremos a e b:
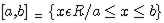Intervalo fechado em a e aberto em b:
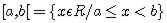Intervalo aberto em a e fechado em b:
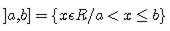Intervalo aberto em a e b:
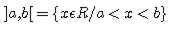Temos também:
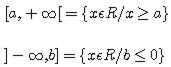
Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...}
É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá como resultado um número natural, já a subtração entre dois números naturais nem sempre é um número natural, como por exemplo 2 - 5, não pertence aos N, temos então o surgimento do conjunto dos números inteiros.
No conjunto dos inteiros destacamos os seguintes subconjuntos:
Z* = Z - {0} = {...-3,-2,-1,1,2,3...}
Z+ = {0,1,2,3,4...} (inteiros não negativos)
Z - = {0,-1,-2,-3,-4...} (inteiros não positivos)
Z*+ = {1,2,3,4...} (inteiros positivos)
Z*- = {-1,-2,-3,-4...} (inteiros não negativos)
Neste conjunto sempre é possível efetuar a adição, a multiplicação e a subtração entre números inteiros, isto é, sempre estas operações resultam em um número inteiro. Já a divisão nem sempre resulta em um número inteiro, como por exemplo, 7 : 2 ,não pertence aos inteiros surgindo assim o conjunto dos racionais.
O conjunto dos números racionais Q é a união do conjunto dos números naturais (N), inteiros (Z) e as frações positivas e negativas, como por exemplo:
Q = -5 ; - 4/3 ; - 1; 0; 0,25 ; 1/2 ; 3/4 ; 1; 6/5 ; 2
Obs: Um número racional pode aparecer em forma de dízima periódica, isto é, um numeral decimal, com a parte decimal formada por infinitos algarismos que se repetem periodicamente, como por exemplo: 4,5555 (período 5) , 10,878787 (período 87) e 9,8545454... (período 54, parte não periódica 8)
Exemplo: transformar em frações irredutíveis os números:
a) 0,1111....
x=0,111...
10x=1,111...
daí,
10x-x=1
x=1/9
portanto, 0,111...=1/9
b) 2,1343434...
x=2,1343434...
10x=21,3434...
1000x=2134,3434....
daí,
1000x-10x=2113
x=2113/990
portanto, 2,1343434...=2113/990
- raiz quadrada de três = 1,73...;
- dízimas não periódicas;
- Conjunto Dos Números Naturais
Representação dos números naturaisConjunto é a reunião de elementos que têm características em comum. Por exemplo: se pegarmos a reunião dos alunos do 6° ano de um colégio, irá pertencer a esse conjunto somente os alunos do 6° ano, qualquer...
- Conjuntos Teoria
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com No estudo de Conjuntos, trabalhamos com alguns conceitos primitivos, que ...
- Conjuntos
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comAlguns...
- Conjunto
Ele representa conjuntos da seguinte maneira: a) b) Relação de inclusão – SubconjuntoDados dois conjuntos A e B, diz que A está contido em B ou que A é subconjunto de B, somente se, todo elemento do conjunto A também for elemento de B. Isso será...
- Conjunto
►Conjunto unitário e conjunto vazio Por exemplo: A = { x | x é par e 4 < x < 8 } ou A = {6} B = { x | 2x + 1 = 7 e x é inteiro } ou B = {3} Os dois conjuntos acima são exemplos de conjuntos unitários. Pois possuem apenas um elemento. Dado...
Matemática
conjuntos
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
Blog HTTP://ensinodematemtica.blogspot.com.br
http://accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.com
http://accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.com
Alguns conceitos primitivos
Conjunto
O conjunto de todos os brasileiros.O conjunto de todos os números naturais.
O conjunto dos números reais tal que x2-4=0.
Em geral, um conjunto é denotado por uma letra maiúscula do alfabeto: A, B, C, ..., Z.
Elemento
José da Silva é um elemento do conjunto dos brasileiros.1 é um elemento do conjunto dos números naturais.
-2 é um elemento do conjunto dos números reais que satisfaz à equação x2-4=0.
Em geral, um elemento de um conjunto, é denotado por uma letra minúscula do alfabeto: a, b, c, ..., z.
Pertinência
José da Silva pertence ao conjunto dos brasileiros.1 pertence ao conjunto dos números naturais.
-2 pertence ao conjunto de números reais que satisfaz à equação x2-4=0.
Se um elemento pertence a um conjunto utilizamos o símbolo
, que se lê: "pertence".Para afirmar que 1 é um número natural, escrevemos:
1NPara afirmar que 0 não é um número natural, escrevemos:
0
NUm símbolo matemático para a negação é a barra /.
Algumas notações para conjuntos
Muitas vezes, um conjunto é representado com os seus elementos dentro de duas chaves { e } através de duas formas básicas e de uma terceira forma geométrica:Apresentação: Os elementos do conjunto estão dentro de duas chaves { e }.
A = { a, e, i, o, u }
N = { 1, 2, 3, 4, ... }
M = { João, Maria, José }
Descrição: O conjunto é descrito por uma ou mais propriedades.
A = { x : x é uma vogal}
N = { x : x é um número natural}
M = { x : x é uma pessoa da família de Maria}
Diagrama de Venn-Euler (lê-se: "Ven-óiler"): Os conjuntos são mostrados graficamente
Subconjuntos
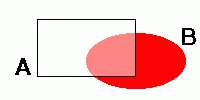
Dados os conjuntos A e B, diz-se que A está contido em B, denotado por AB, se todos os elementos de A também estão em B. Algumas vezes diremos que um conjunto A está propriamente contido em B, quando o conjunto B, além de conter os elementos de A, contém também outros elementos. O conjunto A é denominado subconjunto de B e o conjunto B é o superconjunto que contém A.Alguns conjuntos especiais
Conjunto vazio: É um conjunto que não possui elementos. É representado por { } ou por Ø. O conjunto vazio está contido em todos os conjuntos.Conjunto universo: É um conjunto que contém todos os elementos do contexto no qual estamos trabalhando e também contém todos os conjuntos desse contexto. O conjunto universo é representado por uma letra U. Na sequência não mais usaremos o conjunto universo.
Reunião de conjuntos
A reunião dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A ou ao conjunto B.A
B = { x: aA ou xB }Interseção de conjuntos
A interseção dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e ao conjunto B.A
B = { x: aA e xB }Quando a interseção de dois conjuntos A e B é o conjunto vazio, dizemos que estes conjuntos são disjuntos.
Propriedades dos conjuntos
Fechamento: Quaisquer que sejam os conjuntos A e B, a reunião de A e B, denotada por AB e a interseção de A e B, denotada por AB, ainda são conjuntos no universo.Reflexiva: Qualquer que seja o conjunto A, tem-se que:
A
A = A e A A = A1. Inclusão: Quaisquer que sejam os conjuntos A e B, tem-se que:
A
AB, BAB, ABA, ABB2. Inclusão relacionada: Quaisquer que sejam os conjuntos A e B, tem-se que:
A
B equivale a AB = BA
B equivale a AB = A 3. Associativa: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A
(BC) = (AB)CA
(BC) = (AB)C4. Comutativa: Quaisquer que sejam os conjuntos A e B, tem-se que:
A
B = BAA
B = BA5. Elemento neutro para a reunião: O conjunto vazio Ø é o elemento neutro para a reunião de conjuntos, tal que para todo conjunto A, se tem:
A
Ø = A6. Elemento "nulo" para a interseção: A interseção do conjunto vazio Ø com qualquer outro conjunto A, fornece o próprio conjunto vazio.
A
Ø = Ø7. Elemento neutro para a interseção: O conjunto universo U é o elemento neutro para a interseção de conjuntos, tal que para todo conjunto A, se tem:
A
U = A8. Distributiva: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A
( B C ) = ( A B ) ( A C )A
( B C ) = ( A B ) (A C )Os gráficos abaixo mostram a distributividade.
Diferença de conjuntos
A diferença entre os conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.A-B = { x: a
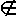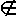e x BDo ponto de vista gráfico, a diferença pode ser vista como:
Complemento de um conjunto
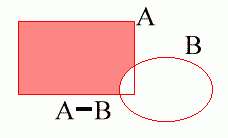
O complemento do conjunto B contido no conjunto A, denotado por C BA, é a diferença entre os conjuntos A e B, ou seja, é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.C BA = A-B = { x: x
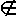A e x B }Graficamente, o complemento do conjunto B no conjunto A, é dado por:
Leis de Augustus De Morgan
O complementar da reunião de dois conjuntos é a interseção dos complementares desses conjuntos.(A
B)c = Ac BcO complementar da reunião de uma coleção finita de conjuntos é a interseção dos complementares desses conjuntos.
(A1
A2 ... An)c = A1c A2c ... AncO complementar da interseção de dois conjuntos é a reunião dos complementares desses conjuntos.
(A
B)c = Ac BcDiferença simétrica
A diferença simétrica entre os conjuntos A e B é o conjunto de todos os elementos que pertencem à reunião dos conjuntos A e B e não pertencem à interseção dos conjuntos A e B.A
B = { x: xAB e xAB }A situação gráfica para a diferença simétrica é:
1. A=Ø se, e somente se, B=A
B.2. O conjunto vazio é o elemento neutro para a operação de diferença simétrica. Usar o ítem anterior.
3. A diferença simétrica é comutativa.
4. A diferença simétrica é associativa.
5. A
A=Ø (conjunto vazio).6. A interseção entre A e B
C é distributiva, isto é:A
(BC) = (AB)(AC)7. A
B está contida na reunião de AC e de BC, mas esta inclusão é própria, isto é:A
B (AC)(BC)conjuntos numéricos
I) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
II) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
Fonte: pessoal.sercomtel.com.br
Conjuntos numéricos
Conjuntos NuméricosI) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
II) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
Todo número natural é inteiro, isto é, N é um subconjunto de Z |
- São aqueles que podem ser expressos na forma a/b, onde a e b são inteiros quaisquer, com b diferente de 0.
Q ={x/x = a/b com a e b pertencentes a Z com b diferente de 0 } |
-Números decimais exatos são racionais
Pois 0,1 = 1/10
2,3 = 23/10 ...
- Números decimais periódicos são racionais.
0,1111... = 1/9
0,3232 ...= 32/99
2,3333 ...= 21/9
0,2111 ...= 19/90
-Toda dízima periódica 0,9999 ... 9 ... é uma outra representação do número 1.
IV) Números Irracionais
- São aqueles que não podem ser expressos na forma a/b, com a e b inteiros e b diferente de 0.-São compostos por dízimas infinitas não periódicas.
Exs: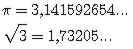 
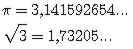
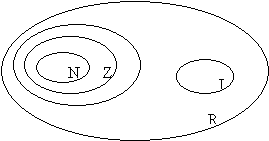
V) Números Reais
- É a reunião do conjunto dos números irracionais com o dos racionais.Resumindo:
Intervalos :
Sendo a e b dois números reais, com a <>Intervalo fechado nos extremos a e b:
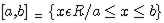
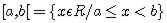
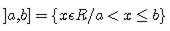
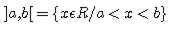
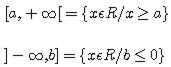
Fonte: www.exatas.hpg.ig.com.br
Conjuntos Numéricos
1- Naturais (IN)
N = {0,1,2,3,4,5...}Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...}
É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá como resultado um número natural, já a subtração entre dois números naturais nem sempre é um número natural, como por exemplo 2 - 5, não pertence aos N, temos então o surgimento do conjunto dos números inteiros.
2- Inteiros (Z)
Z = {...-3,-2,-1,0,1,2,3...}No conjunto dos inteiros destacamos os seguintes subconjuntos:
Z* = Z - {0} = {...-3,-2,-1,1,2,3...}
Z+ = {0,1,2,3,4...} (inteiros não negativos)
Z - = {0,-1,-2,-3,-4...} (inteiros não positivos)
Z*+ = {1,2,3,4...} (inteiros positivos)
Z*- = {-1,-2,-3,-4...} (inteiros não negativos)
Neste conjunto sempre é possível efetuar a adição, a multiplicação e a subtração entre números inteiros, isto é, sempre estas operações resultam em um número inteiro. Já a divisão nem sempre resulta em um número inteiro, como por exemplo, 7 : 2 ,não pertence aos inteiros surgindo assim o conjunto dos racionais.
3-Racionais (Q)
Q = {x tal que x = a/b (a sobre b) onde aÎ (pertence) Z a b E Z* (Z menos o zero)}.O conjunto dos números racionais Q é a união do conjunto dos números naturais (N), inteiros (Z) e as frações positivas e negativas, como por exemplo:
Q = -5 ; - 4/3 ; - 1; 0; 0,25 ; 1/2 ; 3/4 ; 1; 6/5 ; 2
Obs: Um número racional pode aparecer em forma de dízima periódica, isto é, um numeral decimal, com a parte decimal formada por infinitos algarismos que se repetem periodicamente, como por exemplo: 4,5555 (período 5) , 10,878787 (período 87) e 9,8545454... (período 54, parte não periódica 8)
Exemplo: transformar em frações irredutíveis os números:
a) 0,1111....
x=0,111...
10x=1,111...
daí,
10x-x=1
x=1/9
portanto, 0,111...=1/9
b) 2,1343434...
x=2,1343434...
10x=21,3434...
1000x=2134,3434....
daí,
1000x-10x=2113
x=2113/990
portanto, 2,1343434...=2113/990
4-Irracionais (I) - É todo número decimal não-exato e não periódico, bem como toda raiz não-exata.
- raiz quadrada de dois = 1,414...;- raiz quadrada de três = 1,73...;
- dízimas não periódicas;
5-Reais (IR)
Fonte: www.ficharionline.com
- Conjunto Dos Números Naturais
Representação dos números naturaisConjunto é a reunião de elementos que têm características em comum. Por exemplo: se pegarmos a reunião dos alunos do 6° ano de um colégio, irá pertencer a esse conjunto somente os alunos do 6° ano, qualquer...
- Conjuntos Teoria
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com No estudo de Conjuntos, trabalhamos com alguns conceitos primitivos, que ...
- Conjuntos
Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso Colégio Estadual Dinah Gonçalves email [email protected] HTTP://ensinodematemtica.blogspot.com.br http://accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.comAlguns...
- Conjunto
Ele representa conjuntos da seguinte maneira: a) b) Relação de inclusão – SubconjuntoDados dois conjuntos A e B, diz que A está contido em B ou que A é subconjunto de B, somente se, todo elemento do conjunto A também for elemento de B. Isso será...
- Conjunto
►Conjunto unitário e conjunto vazio Por exemplo: A = { x | x é par e 4 < x < 8 } ou A = {6} B = { x | 2x + 1 = 7 e x é inteiro } ou B = {3} Os dois conjuntos acima são exemplos de conjuntos unitários. Pois possuem apenas um elemento. Dado...