Matemática

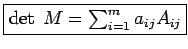 em que
em que 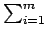 é o somatório de todos os termos de índice
é o somatório de todos os termos de índice  , variando de 1 até
, variando de 1 até 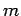 ,
, 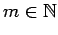 .
.
O primeiro teorema de Laplace afirma que “o determinante de uma matriz quadrada A é igual à soma dos elementos de qualquer linha de seus complementos algébricos”.
 para toda a linha.
para toda a linha.
Da mesma forma, o segundo teorema de Laplace afirma que “o determinante de uma matriz quadrada A é igual à soma dos elementos de qualquer coluna para o seu complemento algébrico”.
Assim, através da fórmula,

para qualquer coluna j
Conclui-se a partir daí que:
a) O determinante de uma matriz diagonal é o produto dos valores na diagonal.
b) O determinante de uma matriz triangular é ainda o produto da diagonal.
c) Os autovalores de uma matriz triangular são os elementos na diagonal.
Um caso concreto de aplicação do Teorema de Laplace refere-se ao produto vetorial partindo de dois vetores “u” e “v”:

temos então o produto vectorial de ambos como outro vetor:

Que se calcula com a seguinte determinante:

Desenvolvendo-se por meio do Teorema de Laplace:

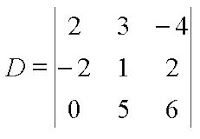
Aplicando o Teorema de Laplace na coluna 1, temos:
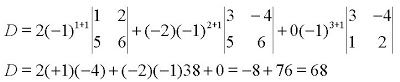
REFERÊNCIAS
http://www.mundofisico.joinville.udesc.br
http://w3.ualg.pt/~gmarques/Ficheiros/determinantes25-29-w.pdf
http://www.infoescola.com
- O Teorema De Laplace
O Teorema de LaplaceMarcelo Rigonatto DeterminanteO teorema de Laplace consiste num método de calcular o determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator. Lembrando que o cofator do elemento aij de uma matriz...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Determinantes Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn). A toda matriz quadrada está associado um número ao qual damos o nome de determinante. Dentre as várias aplicações dos...
- Propriedades Dos Determinantes
Propriedades dos determinantesMarcelo Rigonatto DeterminantesO cálculo dos determinantes pode ser facilitado se analisarmos as características e propriedades de algumas matrizes. Há algumas propriedades que, se bem observadas,...
- Determinante
a) Menor complementar O menor complementar de um elemento é o determinante da sua matriz quadrada. Para obtermos o menor complementar basta eliminar a linha e a coluna que o elemento pertence. Obs.: todos elementos de uma matriz possui um menor complementar....
Matemática
Determinantes: Teorema de Laplace

Pierre Simon, Marquis de Laplace (Beaumont-en-Auge, 23 de março de 1749 — Paris, 5 de março de 1827) foi um matemático, astrônomo e físico francês que organizou a astronomia matemática, sumarizando e ampliando o trabalho de seu predecessores nos cinco volumes do seu Mécanique Céleste (Mecânica celeste) (1799-1825). Esta obra-prima traduziu o estudo geométrico da mecânica clássica usada por Isaac Newton para um estudo baseado em cálculo, conhecido como mecânica física.
Ele também formulou a equação de Laplace. A transformada de Laplace aparece em todos os ramos da física matemática, campo em que teve um papel principal na formação. O operador diferencial de Laplace, da qual depende muito a matemática aplicada, também recebe seu nome.
Ele se tornou conde do Império em 1806 e foi nomeado marquês em 1817, depois da restauração dos Bourbons.
No campo da álgebra linear, o teorema de Laplace, é um teorema matemático utilizado para simplificar o cálculo de determinantes em matriz quadrada, proporcionando a possibilidade de decompô-lo em números menores.
Determinante é o número que se associa a uma matriz quadrada; de modo geral, um determinante é indicado escrevendo-se os elementos da matriz entre barras ou antepondo a matriz o símbolo “det”.
Para aplicar o teorema de Laplace é necessário escolher uma fila (linha ou coluna da matriz), adicionando desse modo os produtos dos elementos desta fila ao cofatores correspondentes.
O determinante de uma matriz quadrada ![$ M={[a_{ij}]}_{m \times n} \; (m \geq 2)$](matematica/matematica-57ac2482b95db.png) pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz 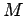 pelos respectivos cofatores.
pelos respectivos cofatores.
![$ M={[a_{ij}]}_{m \times n} \; (m \geq 2)$](matematica/matematica-57ac2482b95db.png) pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz 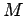 pelos respectivos cofatores.
pelos respectivos cofatores. Desta forma, fixando 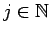 , tal que
, tal que 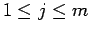 , temos:
, temos:
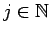 , tal que
, tal que 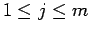 , temos:
, temos: 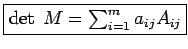
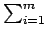 é o somatório de todos os termos de índice
é o somatório de todos os termos de índice  , variando de 1 até
, variando de 1 até 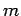 ,
, 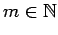 .
.Através do desenvolvimento do teorema de Laplace podemos desenvolver o determinante n X n-matriz depois de uma linha ou coluna. Assim, a seguir, teremos duas fórmulas.

Da mesma forma, o segundo teorema de Laplace afirma que “o determinante de uma matriz quadrada A é igual à soma dos elementos de qualquer coluna para o seu complemento algébrico”.
Assim, através da fórmula,

para qualquer coluna j
Conclui-se a partir daí que:
a) O determinante de uma matriz diagonal é o produto dos valores na diagonal.
b) O determinante de uma matriz triangular é ainda o produto da diagonal.
c) Os autovalores de uma matriz triangular são os elementos na diagonal.
Um caso concreto de aplicação do Teorema de Laplace refere-se ao produto vetorial partindo de dois vetores “u” e “v”:

temos então o produto vectorial de ambos como outro vetor:

Que se calcula com a seguinte determinante:

Desenvolvendo-se por meio do Teorema de Laplace:

Exemplo:
Calcule o determinante a seguir utilizando o Teorema de Laplace:
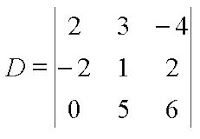
Aplicando o Teorema de Laplace na coluna 1, temos:
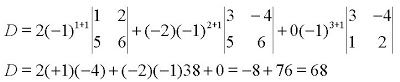
Observação
Se calcularmos o determinante utilizando a Regra de Sarrus, obteremos o mesmo número real.REFERÊNCIAS
http://www.mundofisico.joinville.udesc.br
http://w3.ualg.pt/~gmarques/Ficheiros/determinantes25-29-w.pdf
http://www.infoescola.com
- O Teorema De Laplace
O Teorema de LaplaceMarcelo Rigonatto DeterminanteO teorema de Laplace consiste num método de calcular o determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator. Lembrando que o cofator do elemento aij de uma matriz...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Determinantes Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo nxn). A toda matriz quadrada está associado um número ao qual damos o nome de determinante. Dentre as várias aplicações dos...
- Propriedades Dos Determinantes
Propriedades dos determinantesMarcelo Rigonatto DeterminantesO cálculo dos determinantes pode ser facilitado se analisarmos as características e propriedades de algumas matrizes. Há algumas propriedades que, se bem observadas,...
- Determinante
a) Menor complementar O menor complementar de um elemento é o determinante da sua matriz quadrada. Para obtermos o menor complementar basta eliminar a linha e a coluna que o elemento pertence. Obs.: todos elementos de uma matriz possui um menor complementar....
