Matemática
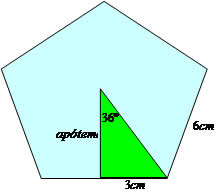tg 36º = 3/a
0,727 = 3/a
a = 3/0,727
a = 4,1
Perímetro do pentágono:
6 x 5 = 30
Aplicando a fórmula para área do pentágono A = (a*P)/2, temos:
A = (4,1*30)/2
A = 61,5 cm²
Área do dodecaedro que possui arestas medindo 6 cm:
61,5 x 12 = 738 cm²
A área do dodecaedro também pode ser dada pela expressão:
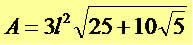
O volume é dado pela expressão:
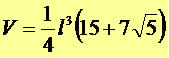
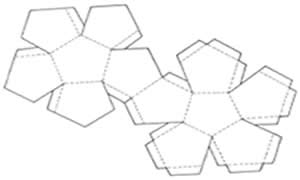
Planificação do dodecaedro
www.mundoeducacao.com.br
- Questão 42 ? Processo De Promoção ? Qm ? Professor De Matemática ? See/sp ? 2.015
Carl B. Boyer destina um dos capítulos de seu livro História da Matemática ao desenvolvimento dessa área do conhecimento no período correspondente à época de Aristóteles e de Platão. Nesse capítulo são apresentados os cinco sólidos platônicos...
- Por Que Só Existem 5 Sólidos Platônicos?
Essa pergunta pode ser comum para muitos estudantes durante sua vida, pelo menos para mim foi. Quando estudamos Geometria Espacial nos deparamos com esses sólidos bem peculiares descobrimos que só existem apenas cinco deles, mas por quê? É isso que...
- Poliedros
Poliedros são sólidos geométricos ou figuras geométricas espaciais formadas por três elementos básicos: faces, arestas e vértices. Os Poliedros podem ser convexos e não convexos. Ao estudarmos os poliedros convexos verificamos uma importante relação...
- Os Sólidos De Platão
Os sólidos de Platão também são denominados de poliedros, pois são formados por faces, arestas e vértices. As faces são constituídas por seções de planos, considerando que entre duas faces temos as arestas, as quais possuem em suas extremidades...
- Pirâmides
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados...
Matemática
Dodecaedro Regular
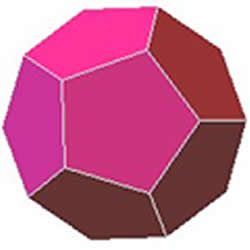
Dodecaedro: sólido platônico
O mais harmonioso e soberano dos sólidos Platônicos é o dodecaedro que, segundo Platão, representa o universo ou o cosmos. É constituído por doze pentágonos e não se divide em outros poliedros regulares. Possui 30 arestas, 20 vértices e 12 faces pentagonais.
Para calcularmos a área total de um dodecaedro precisamos levar em conta a área do pentágono, que é dada pela seguinte expressão A = (a*P)/2, onde a: medida do apótema do pentágono (depende do tamanho do lado) e P: perímetro do pentágono (depende do tamanho do lado). Calculada a área do pentágono, basta multiplicar por doze - que é o número de faces pentagonais do dodecaedro.
Para calcularmos a área total de um dodecaedro precisamos levar em conta a área do pentágono, que é dada pela seguinte expressão A = (a*P)/2, onde a: medida do apótema do pentágono (depende do tamanho do lado) e P: perímetro do pentágono (depende do tamanho do lado). Calculada a área do pentágono, basta multiplicar por doze - que é o número de faces pentagonais do dodecaedro.
0,727 = 3/a
a = 3/0,727
a = 4,1
Perímetro do pentágono:
6 x 5 = 30
Aplicando a fórmula para área do pentágono A = (a*P)/2, temos:
A = (4,1*30)/2
A = 61,5 cm²
Área do dodecaedro que possui arestas medindo 6 cm:
61,5 x 12 = 738 cm²
A área do dodecaedro também pode ser dada pela expressão:
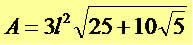
O volume é dado pela expressão:
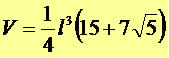
Planificação do dodecaedro
www.mundoeducacao.com.br
- Questão 42 ? Processo De Promoção ? Qm ? Professor De Matemática ? See/sp ? 2.015
Carl B. Boyer destina um dos capítulos de seu livro História da Matemática ao desenvolvimento dessa área do conhecimento no período correspondente à época de Aristóteles e de Platão. Nesse capítulo são apresentados os cinco sólidos platônicos...
- Por Que Só Existem 5 Sólidos Platônicos?
Essa pergunta pode ser comum para muitos estudantes durante sua vida, pelo menos para mim foi. Quando estudamos Geometria Espacial nos deparamos com esses sólidos bem peculiares descobrimos que só existem apenas cinco deles, mas por quê? É isso que...
- Poliedros
Poliedros são sólidos geométricos ou figuras geométricas espaciais formadas por três elementos básicos: faces, arestas e vértices. Os Poliedros podem ser convexos e não convexos. Ao estudarmos os poliedros convexos verificamos uma importante relação...
- Os Sólidos De Platão
Os sólidos de Platão também são denominados de poliedros, pois são formados por faces, arestas e vértices. As faces são constituídas por seções de planos, considerando que entre duas faces temos as arestas, as quais possuem em suas extremidades...
- Pirâmides
Dada uma região poligonal de n vértices e um ponto V fora da região (outro plano), ao traçarmos segmentos de retas entre os vértices da região poligonal e o ponto V, construímos uma pirâmide que será classificada de acordo com o número de lados...