Matemática
Em um plano cartesiano as retas podem ser paralelas ou coincidentes, se no ponto comum as duas retas formarem um ângulo de 90° graus podemos dizer que são perpendiculares, para que isso seja verdade os seus coeficientes deverão ser o oposto do inverso um do outro. Veja alguns exemplos onde aplicamos essa comparação dos coeficientes de duas retas coincidentes e perpendiculares.
Exemplo 1: obtenha a equação geral da reta t que passa pelo ponto P(9,-1) e é perpendicular à reta s: y = x/5 + 2.
Resolução
A reta s tem equação reduzida igual a y = x/5 + 2, nela podemos identificar o coeficiente angular de s: ms = 1/5. Como foi dito no enunciado que as retas s e t são perpendiculares, podemos considerar as seguintes informações pertencentes à reta t:
t: P(9,-1) e seu coeficiente será o oposto do inverso do coeficiente da reta s: mt = -5. Com essas informações e utilizando a definição de equação fundamental da reta podemos encontrar a equação geral da reta t.
y – y0 = m(x – x0)
y – (-1) = -5(x – 9)
y + 1 = - 5x + 45
5x + y – 45 = 0 é a equação geral da reta t.
Exemplo 2: Considerando o gráfico:
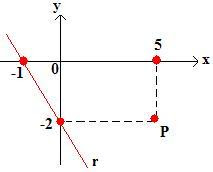
Responda:
a) Obtenha uma equação da reta r.
Com os pontos pertencentes à reta r, podemos calcular seu coeficiente que será igual à mr = -2, com esse valor mais um dos dois pontos e utilizando a definição de equação fundamental da reta, a reta r terá a seguinte equação:
y – y0 = m(x – x0)
y – 0 = - 2(x + 1)
2x – y – 2 = 0
b) Obtenha a equação da reta s que passa pelo ponto P e é perpendicular à reta r.
Como as retas r e s são perpendiculares e o coeficiente da reta r é mr = -2, podemos concluir pela definição de coeficiente de retas paralelas que o coeficiente da reta s será ms = 1/2, como o ponto P pertence à reta s, concluímos pela definição da equação fundamental da reta, que a reta s terá equação igual a:
y – y0 = m(x – x0)
y + 2 = 1/2 (x – 5)
y + 2 = x/2 – 5/2
x – 2y – 9 = 0
c) Determinar o ponto A (x,y) de interseção de r com a reta s obtida no item b.
O ponto A irá pertencer à reta r e para que esse mais os outros dois pontos pertençam à reta r eles deverão obedecer à condição de alinhamento de três pontos, que diz que os coeficientes angulares das semi-retas formadas pelos pontos deverão ser iguais. Assim iremos obter uma equação em função dos valores do ponto A (x,y).
-2x – y = 2
O ponto A e P pertencem à reta s, com eles é possível calcular o coeficiente angular da reta s:
y + 2 = 1
x – 5 2
x – 2y = 9
Com essas duas equações podemos formar um sistema que terá como solução o par ordenado (1,-4) que corresponde ao ponto A.
- Retas Paralelas
No estudo analítico da reta não podemos deixar de falar das posições relativas entre retas. Dadas duas ou mais retas do plano, elas podem ser paralelas, concorrentes, coincidentes ou concorrentes perpendiculares. Abordaremos aqui o paralelismo de...
- Equação Da Reta
A equação reduzida da reta deixa explícito o coeficiente angular e o ponto que a reta intercepta o eixo Oy. Essa nova equação da reta foi determinada a partir da equação fundamental da reta que é determinada por um ponto (x0, y0) pertencente a...
- Equação Da Reta
Toda reta não-vertical (reta que possui inclinação diferente de 90º) possui uma equação que representa todos os seus pontos. Essa equação é demonstrada através de um ponto pertencente a essa reta mais o seu coeficiente angular (m). Considere...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
- Equação Fundamental Da Reta
Com um ponto e um ângulo podemos indicar e construir uma reta. E se a reta formada não for vertical (reta vertical é perpendicular ao eixo Ox) com o ponto pertencente a ela mais o seu coeficiente angular (tangente do ângulo de inclinação) é possível...
Matemática
Equação da reta
Em um plano cartesiano as retas podem ser paralelas ou coincidentes, se no ponto comum as duas retas formarem um ângulo de 90° graus podemos dizer que são perpendiculares, para que isso seja verdade os seus coeficientes deverão ser o oposto do inverso um do outro. Veja alguns exemplos onde aplicamos essa comparação dos coeficientes de duas retas coincidentes e perpendiculares.
Exemplo 1: obtenha a equação geral da reta t que passa pelo ponto P(9,-1) e é perpendicular à reta s: y = x/5 + 2.
Resolução
A reta s tem equação reduzida igual a y = x/5 + 2, nela podemos identificar o coeficiente angular de s: ms = 1/5. Como foi dito no enunciado que as retas s e t são perpendiculares, podemos considerar as seguintes informações pertencentes à reta t:
t: P(9,-1) e seu coeficiente será o oposto do inverso do coeficiente da reta s: mt = -5. Com essas informações e utilizando a definição de equação fundamental da reta podemos encontrar a equação geral da reta t.
y – y0 = m(x – x0)
y – (-1) = -5(x – 9)
y + 1 = - 5x + 45
5x + y – 45 = 0 é a equação geral da reta t.
Exemplo 2: Considerando o gráfico:
Responda:
a) Obtenha uma equação da reta r.
Com os pontos pertencentes à reta r, podemos calcular seu coeficiente que será igual à mr = -2, com esse valor mais um dos dois pontos e utilizando a definição de equação fundamental da reta, a reta r terá a seguinte equação:
y – y0 = m(x – x0)
y – 0 = - 2(x + 1)
2x – y – 2 = 0
b) Obtenha a equação da reta s que passa pelo ponto P e é perpendicular à reta r.
Como as retas r e s são perpendiculares e o coeficiente da reta r é mr = -2, podemos concluir pela definição de coeficiente de retas paralelas que o coeficiente da reta s será ms = 1/2, como o ponto P pertence à reta s, concluímos pela definição da equação fundamental da reta, que a reta s terá equação igual a:
y – y0 = m(x – x0)
y + 2 = 1/2 (x – 5)
y + 2 = x/2 – 5/2
x – 2y – 9 = 0
c) Determinar o ponto A (x,y) de interseção de r com a reta s obtida no item b.
O ponto A irá pertencer à reta r e para que esse mais os outros dois pontos pertençam à reta r eles deverão obedecer à condição de alinhamento de três pontos, que diz que os coeficientes angulares das semi-retas formadas pelos pontos deverão ser iguais. Assim iremos obter uma equação em função dos valores do ponto A (x,y).
-2x – y = 2
O ponto A e P pertencem à reta s, com eles é possível calcular o coeficiente angular da reta s:
y + 2 = 1
x – 5 2
x – 2y = 9
Com essas duas equações podemos formar um sistema que terá como solução o par ordenado (1,-4) que corresponde ao ponto A.
- Retas Paralelas
No estudo analítico da reta não podemos deixar de falar das posições relativas entre retas. Dadas duas ou mais retas do plano, elas podem ser paralelas, concorrentes, coincidentes ou concorrentes perpendiculares. Abordaremos aqui o paralelismo de...
- Equação Da Reta
A equação reduzida da reta deixa explícito o coeficiente angular e o ponto que a reta intercepta o eixo Oy. Essa nova equação da reta foi determinada a partir da equação fundamental da reta que é determinada por um ponto (x0, y0) pertencente a...
- Equação Da Reta
Toda reta não-vertical (reta que possui inclinação diferente de 90º) possui uma equação que representa todos os seus pontos. Essa equação é demonstrada através de um ponto pertencente a essa reta mais o seu coeficiente angular (m). Considere...
- Equação Fundamental Da Reta
Podemos determinar a equação fundamental de uma reta utilizando o ângulo formado pela reta com o eixo das abscissas (x) e as coordenadas de um ponto pertencente à reta. O coeficiente angular da reta, associado à coordenada do ponto, facilita a representação...
- Equação Fundamental Da Reta
Com um ponto e um ângulo podemos indicar e construir uma reta. E se a reta formada não for vertical (reta vertical é perpendicular ao eixo Ox) com o ponto pertencente a ela mais o seu coeficiente angular (tangente do ângulo de inclinação) é possível...
