Matemática
DEFINIÇÃO
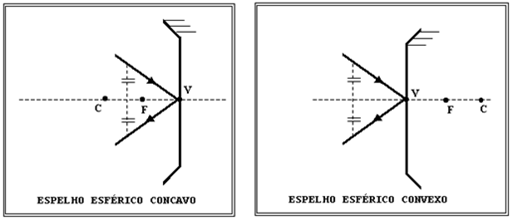
Chamamos de Espelhos Esféricos toda superfície refletora com a forma de uma calota esférica. Temos dois tipos de espelhos esféricos: Côncavo e Convexo.
ESPELHO ESFÉRICO CÔNCAVO é aquele espelho cuja face interna da calota é refletora de luz.

ESPELHO ESFÉRICO CONVEXO é aquele espelho cuja face externa da calota é refletora de luz
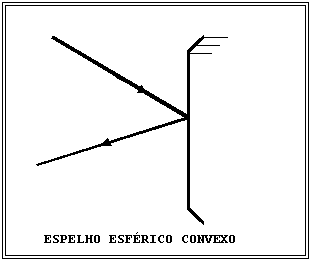
PRINCIPAIS ELEMENTOS DE UM ESPELHO ESFÉRICO
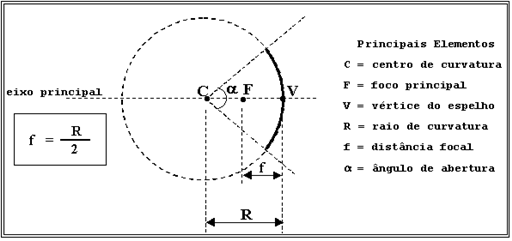
CONDIÇÕES DE NITIDEZ DE GAUSS
I ) Se um raio de luz incidir paralelamente ao eixo principal, o raio refletido passa pelo foco principal.
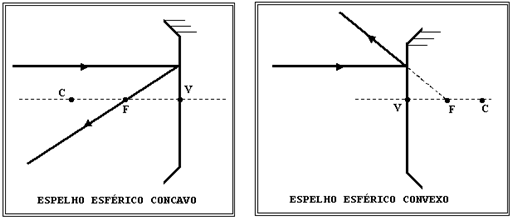
II ) Se um raio de luz incidir passando pelo centro de curvatura, o raio é refletido passando sobre si mesmo.
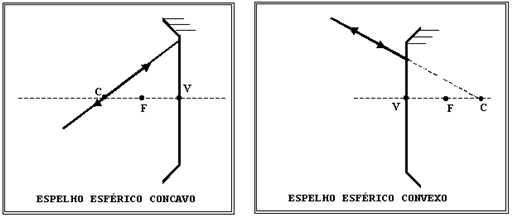
III ) Se um raio de luz incidir no vértice do espelho, o raio refletido é simétrico em relação ao eixo principal.
CONSTRUÇÃO GEOMÉTRICA DE IMAGENS
As imagens fornecidas por um espelho esférico podem ser obtidas utilizando-se dois dos três raios particulares.
A) ESPELHO ESFÉRICO CÔNCAVO
1o Caso: Objeto extenso localizado além do centro de curvatura de um espelho esférico côncavo.
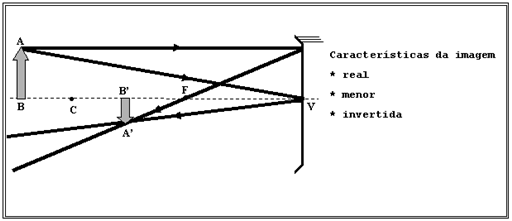
2o Caso: Objeto extenso localizado sobre o centro de curvatura de um espelho esférico côncavo.
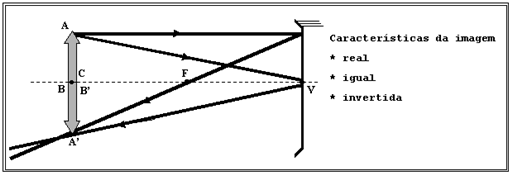
3o Caso: Objeto extenso localizado entre o centro de curvatura e o ponto focal ( F ) de um espelho esférico côncavo.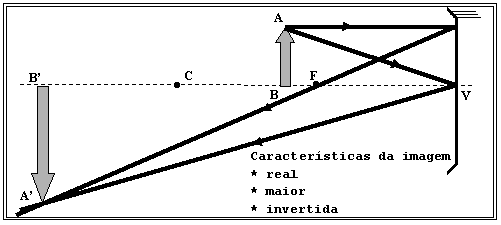
4o Caso: Objeto extenso localizado sobre o ponto focal ( F ) de um espelho esférico côncavo.
5o Caso: Objeto extenso localizado entre o ponto focal ( F ) e o vértice de um espelho esférico côncavo.
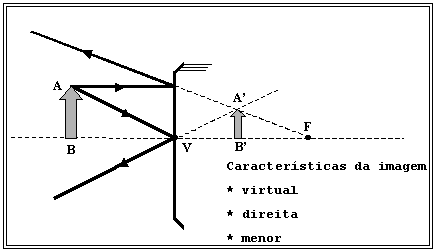
B) ESPELHO ESFÉRICO CONVEXO Objeto extenso localizado em frente a um espelho esférico convexo.
EQUAÇÃO DE GAUSS E EQUAÇÃO DO AUMENTO LINEAR TRANSVERSAL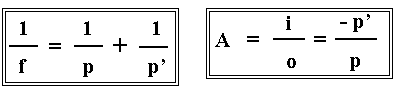
Espelho côncavo f > 0 Espelho convexo f < 0 Imagem real p' > 0 Imagem virtual p' < 0 Imagem direita i > 0 Imagem invertida i <>
www.algosobre.com.br
- Questão 12 ? Vestibulinho Etec ? Centro Paula Souza ? 1° Semestre De 2.013
Em ambulâncias e carros de bombeiros, a comunicação visual é fundamental, já que precisam de rápido reconhecimento pelos motoristas que trafegam à sua frente e que os verão pelo espelho retrovisor...
- Questão 69 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Observe as representações de polígonos. É correto afirmar que apenas (A) a Figura 1 representa um polígono convexo.(B) a Figura 2 representa um polígono convexo.(C) a Figura 3 representa um polígono convexo.(D) as Figuras 1 e 2 representam polígonos...
- Desafio - Elaborado Pelo Professor Flávio Melo
A figura mostra um plano inclinado de altura desconhecida e coeficiente de atrito 0,4 com um bloco de gelo de 1 Kg em seu topo inicialmente em repouso a -2,016°C e uma garrafa térmica contendo um litro de água a 91°C na base do plano inclinado que...
- Tetravista De Z²
As três Tetravistas mostradas na exposição são uma tentativa para entender melhor gráficos de funções complexas. O gráfico duma função de variável complexa está no espaço complexo bidimensional, que pode ser identificado naturalmente com...
- Aplicação De Derivadas No Estudo Sobre A Reflexão E Refração De Um Raio De Luz
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível. Considere um raio de luz que parte de um ponto...
Matemática
Espelhos
DEFINIÇÃO
Chamamos de Espelhos Esféricos toda superfície refletora com a forma de uma calota esférica. Temos dois tipos de espelhos esféricos: Côncavo e Convexo.
ESPELHO ESFÉRICO CÔNCAVO é aquele espelho cuja face interna da calota é refletora de luz.

ESPELHO ESFÉRICO CONVEXO é aquele espelho cuja face externa da calota é refletora de luz

PRINCIPAIS ELEMENTOS DE UM ESPELHO ESFÉRICO

CONDIÇÕES DE NITIDEZ DE GAUSS
O espelho deve ter pequeno ângulo de abertura ( a < 10o )RAIOS PARTICULARES
Os raios incidentes devem ser próximos ao eixo principal.
Os raios incidentes devem ser pouco inclinados em relação ao eixo principal.
I ) Se um raio de luz incidir paralelamente ao eixo principal, o raio refletido passa pelo foco principal.

II ) Se um raio de luz incidir passando pelo centro de curvatura, o raio é refletido passando sobre si mesmo.

III ) Se um raio de luz incidir no vértice do espelho, o raio refletido é simétrico em relação ao eixo principal.

CONSTRUÇÃO GEOMÉTRICA DE IMAGENS
As imagens fornecidas por um espelho esférico podem ser obtidas utilizando-se dois dos três raios particulares.
A) ESPELHO ESFÉRICO CÔNCAVO
1o Caso: Objeto extenso localizado além do centro de curvatura de um espelho esférico côncavo.

2o Caso: Objeto extenso localizado sobre o centro de curvatura de um espelho esférico côncavo.

3o Caso: Objeto extenso localizado entre o centro de curvatura e o ponto focal ( F ) de um espelho esférico côncavo.

4o Caso: Objeto extenso localizado sobre o ponto focal ( F ) de um espelho esférico côncavo.
5o Caso: Objeto extenso localizado entre o ponto focal ( F ) e o vértice de um espelho esférico côncavo.
B) ESPELHO ESFÉRICO CONVEXO Objeto extenso localizado em frente a um espelho esférico convexo.

EQUAÇÃO DE GAUSS E EQUAÇÃO DO AUMENTO LINEAR TRANSVERSAL

f .... distância focal.ATENÇÃO: Considerando sempre o objeto real ( p > 0 ), nestas equações temos:
p .... distância do objeto até o espelho.
p' ... distância da imagem até o espelho.
A ... Aumento linear transversal.
i .... tamanho da imagem.
o .... tamanho do objeto.
Espelho côncavo f > 0 Espelho convexo f < 0 Imagem real p' > 0 Imagem virtual p' < 0 Imagem direita i > 0 Imagem invertida i <>
www.algosobre.com.br
- Questão 12 ? Vestibulinho Etec ? Centro Paula Souza ? 1° Semestre De 2.013
Em ambulâncias e carros de bombeiros, a comunicação visual é fundamental, já que precisam de rápido reconhecimento pelos motoristas que trafegam à sua frente e que os verão pelo espelho retrovisor...
- Questão 69 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Observe as representações de polígonos. É correto afirmar que apenas (A) a Figura 1 representa um polígono convexo.(B) a Figura 2 representa um polígono convexo.(C) a Figura 3 representa um polígono convexo.(D) as Figuras 1 e 2 representam polígonos...
- Desafio - Elaborado Pelo Professor Flávio Melo
A figura mostra um plano inclinado de altura desconhecida e coeficiente de atrito 0,4 com um bloco de gelo de 1 Kg em seu topo inicialmente em repouso a -2,016°C e uma garrafa térmica contendo um litro de água a 91°C na base do plano inclinado que...
- Tetravista De Z²
As três Tetravistas mostradas na exposição são uma tentativa para entender melhor gráficos de funções complexas. O gráfico duma função de variável complexa está no espaço complexo bidimensional, que pode ser identificado naturalmente com...
- Aplicação De Derivadas No Estudo Sobre A Reflexão E Refração De Um Raio De Luz
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível. Considere um raio de luz que parte de um ponto...
