Matemática
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível.
Considere um raio de luz que parte de um ponto $A$ e segue a um ponto $P$ sobre um espelho plano sendo refletido e passando por um ponto $B$. O raio incidente e o raio refletido possuem ângulos iguais a $\alpha$ e $\beta$, respectivamente.
Suponha que o raio de luz siga o caminho mais curto de $A$ a $B$ passando pelo espelho. Provemos que essa lei de reflexão seguindo o caminho $APB$ é mais curto quando $\alpha = \beta$.
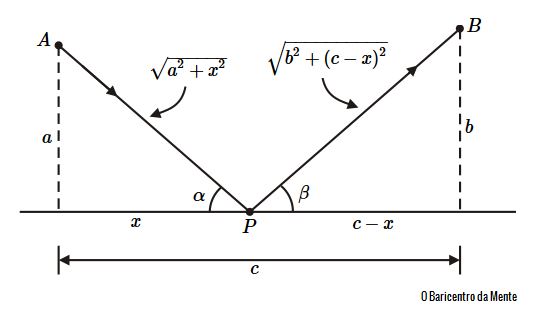
Considere que o ponto $P$ assuma várias posições no espelho, sendo cada posição determinada por um valor de $x$, conforme se pode observar na figura acima. Vamos considerar o comprimento $L$ do percurso do raio de luz como sendo uma função de $x$. Assim, podemos escrever a seguinte expressão:
\begin{equation*}
L = \sqrt{a^2+x^2} + \sqrt{b^2+(c-x)^2} = (a^2+x^2)^{1/2} + \left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
A derivada desta expressão nos leva a:
\begin{equation*}
\frac{dL}{dx} = \frac{1}{2} \left(a^2+x^2\right)^{-1/2} \cdot (2x)+\frac{1}{2}\left[ b^2+(c-x)^2 \right]^{-1/2} \cdot 2(c-x)(-1)
\end{equation*}
\begin{equation}
\frac{dL}{dx} = \frac{x}{\sqrt{a^2+x^2}} - \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Minimizamos o comprimento $L$ igualando a deriva acima a zero, obtendo:
\begin{equation}
\frac{x}{\sqrt{a^2+x^2}} = \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Esta equação nos revela que para os ângulos $\alpha$ e $\beta$ nos dois triângulos retângulos da figura acima, as razões entre a hipotenusa e o lado adjacente são iguais e assim $\alpha$ e $\beta$ são iguais.
Derivando a função $L(x)$ e em seguida igualando a zero, minimizamos o comprimento $L$. Podemos ainda utilizar a relação dada em $(1)$ no teste da segunda derivada:
\begin{equation*}
\frac{d^2L}{dx^2} = \frac{a^2}{(a^2+x^2)^{3/2}} + \frac{b^2}{\left[b^2+(c-x)^2 \right]^{3/2}}
\end{equation*}
Basta observar que a quantidade acima será positiva, já que $a$, $b$ e $c$ são distâncias entre pontos.
Podemos ainda utilizar a trigonometria nos triângulos retângulos da figura acima, de modo que a condição de minimização dada em $(2)$ pode ser escrita como:
\begin{equation*}
\cos(\alpha) = \cos(\beta)
\end{equation*}
O que nos leva a $\alpha = \beta$.
Esta lei de reflexão já era conhecida pelos gregos da Antiguidade, mas o fato de que o raio de luz refletido segue o caminho mais curto foi descoberto muito mais tarde por Heron de Alexandria, no século $I~d.C.$.
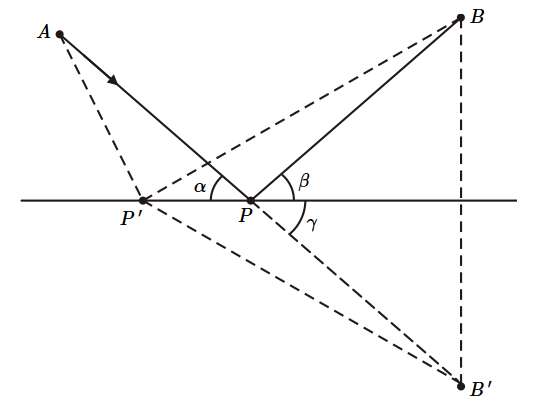
A demonstração de Heron é simples, porém engenhosa: sejam $A$ e $B$ os mesmos pontos da figura anterior, reproduzidos na figura abaixo, e seja $B~^\prime$ a imagem especular de $B$. A superfície do espelho é o plano bissetor de $BB~^\prime$. O segmento $AB~^\prime$ intercepta o espelho num ponto $P$ e este é o ponto onde o raio de luz é refletido ao passar de $A$ para $B$, pois então $\alpha = \gamma$ e $\gamma = \beta$ e assim $\alpha = \beta$. O percurso total do raio de luz é dado por:
\begin{equation*}
AP + PB = AP + PB~^\prime = AB~^\prime
\end{equation*}
O percurso de $A$ a $B$, passando por qualquer outro ponto $P~^\prime$ do espelho é:
\begin{equation*}
AP~^\prime + P~^\prime B = AP~^\prime + P~^\prime B~^\prime
\end{equation*}
que é maior do que o terceiro lado do triângulo $AP~^\prime B~^\prime$, o lado $AB~^\prime $, o que mostra que o percurso real de $A$ para $B$ do raio de luz refletido no espelho é o menor possível.
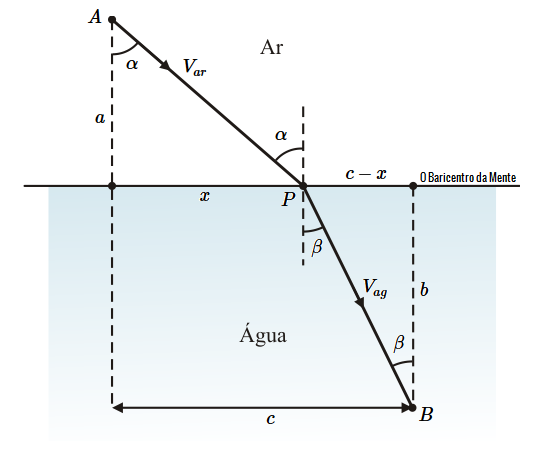
Temos que deixar claro que estes cálculos só tem sentido se considerarmos que o raio de luz tem todo o percurso em um único meio a uma velocidade constante. No entanto, em meios diferentes, como ar, água, vidro, a luz tem velocidades diferentes. Se um raio de luz passa do ar para a água, ele é refratado passando a uma direção mais próxima da perpendicular à interface. O percurso $APB$ não é mais o caminho mais curto de $A$ a $B$.
Em $1621$ o cientista holandês Snell descobriu empiricamente que o caminho real do raio de luz é o que satisfaz a equação:
\begin{equation}
\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \text{constante}
\end{equation}
onde essa constante é independente da posição de $A$ e $B$. Esse fato é chamado de Lei de Refração de Snell. Podemos provar a Lei de Snell partindo do pressuposto de que o raio percorre um caminho de $A$ a $B$ de modo a minimizar o tempo total de percurso.
Seja a velocidade da luz no ar denotada por $V_{ar}$ e na água $V_{ag}$ e seja $T$ o tempo total do percurso, tempo no ar mais o tempo na água:
\begin{equation*}
T = \frac{\sqrt{a^2+x^2}}{V_{ar}} + \frac{\sqrt{b^2+(c-x)^2}}{V_{ag}}\\
\ \\
T = \frac{1}{V_{ar}}\left(a^2+x^2\right)^{1/2} + \frac{1}{V_{ag}}\left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
Se calcularmos a derivada desta função $T(x)$ e observarmos o seu significado em termos da figura acima, obteremos:
\begin{equation*}
\small \frac{dT}{dx} = \frac{1}{V_{ar}} \cdot \frac{1}{2}\cdot \left(a^2+x^2\right)^{-1/2} \cdot 2x + \frac{1}{V_{ag}}\cdot \frac{1}{2}\cdot \left( b^2+(c-x)^2 \right)^{-1/2} \cdot 2(c-x)\cdot (-1)\\
\end{equation*}
\begin{equation}
\frac{dT}{dx} = \frac{1}{V_{ar}}\cdot\frac{x}{\sqrt{a^2+x^2}} - \frac{1}{V_{ag}}\cdot \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
E ainda pela figura acima, temos:
\begin{equation*}
\text{sen}(\alpha) = \frac{x}{\sqrt{a^2+x^2}} \quad \text{e} \quad \text{sen}(\beta)=\frac{c-x}{\sqrt{b^2(c-x)^2}}
\end{equation*}
Substituindo na derivada anterior, obtemos:
\begin{equation*}
\frac{dT}{dx} = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Para obtermos o $T$ mínimo, igualamos essa derivada a zero:
\begin{equation*}
0 = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}\\
\ \\
\frac{\text{sen}(\alpha)}{V_{ar}} = \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Ou ainda:
\begin{equation}
\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \frac{V_{ar}}{V_{ag}}
\end{equation}
Esta é a forma mais reveladora da Lei de Snell porque dá um significado físico da constante que aparece em $(3)$, pois é a razão entre a velocidade da luz no ar e a velocidade (menor) da luz na água. Essa constante é chamada de índice de refração da água. Se substituírmos a água por qualquer outro meio translúcido, como álcool, glicerina, vidro, ... então a constante teráum valor numérico diferente, pois cada meio possui um índice de refração diferente.
Podemos aplicar o teste da segunda derivada em $(4)$ para verificar se $(5)$ realmente minimiza $T$, observando se esta é positiva:
\begin{equation*}
\frac{d^2T}{dx^2} = \frac{1}{V_{ar}}\frac{a^2}{(a^2+x^2)^{3/2}} + \frac{1}{V_{ag}}\frac{b^2}{\left( b^2+(c-x)^2 \right)^{3/2}}>0
\end{equation*}
Usando derivadas para aproximar funções
Aplicação de derivadas para determinação de máximos e mínimos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- O Teorema Da Corda Quebrada De Arquimedes
O matemático árabe Abul Raihan al Biruni atribui a Arquimedes, uma elegante proposição geométrica, chamada teorema da corda quebrada o qual enunciaremos abaixo: Teorema (Arquimedes):Se $AB$ e $BC$ compõem uma corda quebrada $ABC$, onde $BC >...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Aplicação de derivadas no estudo sobre a reflexão e refração de um raio de luz
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível.
Considere um raio de luz que parte de um ponto $A$ e segue a um ponto $P$ sobre um espelho plano sendo refletido e passando por um ponto $B$. O raio incidente e o raio refletido possuem ângulos iguais a $\alpha$ e $\beta$, respectivamente.
Suponha que o raio de luz siga o caminho mais curto de $A$ a $B$ passando pelo espelho. Provemos que essa lei de reflexão seguindo o caminho $APB$ é mais curto quando $\alpha = \beta$.

[Figura 1]
Considere que o ponto $P$ assuma várias posições no espelho, sendo cada posição determinada por um valor de $x$, conforme se pode observar na figura acima. Vamos considerar o comprimento $L$ do percurso do raio de luz como sendo uma função de $x$. Assim, podemos escrever a seguinte expressão:
\begin{equation*}
L = \sqrt{a^2+x^2} + \sqrt{b^2+(c-x)^2} = (a^2+x^2)^{1/2} + \left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
A derivada desta expressão nos leva a:
\begin{equation*}
\frac{dL}{dx} = \frac{1}{2} \left(a^2+x^2\right)^{-1/2} \cdot (2x)+\frac{1}{2}\left[ b^2+(c-x)^2 \right]^{-1/2} \cdot 2(c-x)(-1)
\end{equation*}
\begin{equation}
\frac{dL}{dx} = \frac{x}{\sqrt{a^2+x^2}} - \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Minimizamos o comprimento $L$ igualando a deriva acima a zero, obtendo:
\begin{equation}
\frac{x}{\sqrt{a^2+x^2}} = \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
Esta equação nos revela que para os ângulos $\alpha$ e $\beta$ nos dois triângulos retângulos da figura acima, as razões entre a hipotenusa e o lado adjacente são iguais e assim $\alpha$ e $\beta$ são iguais.
Derivando a função $L(x)$ e em seguida igualando a zero, minimizamos o comprimento $L$. Podemos ainda utilizar a relação dada em $(1)$ no teste da segunda derivada:
\begin{equation*}
\frac{d^2L}{dx^2} = \frac{a^2}{(a^2+x^2)^{3/2}} + \frac{b^2}{\left[b^2+(c-x)^2 \right]^{3/2}}
\end{equation*}
Basta observar que a quantidade acima será positiva, já que $a$, $b$ e $c$ são distâncias entre pontos.
Podemos ainda utilizar a trigonometria nos triângulos retângulos da figura acima, de modo que a condição de minimização dada em $(2)$ pode ser escrita como:
\begin{equation*}
\cos(\alpha) = \cos(\beta)
\end{equation*}
O que nos leva a $\alpha = \beta$.
Esta lei de reflexão já era conhecida pelos gregos da Antiguidade, mas o fato de que o raio de luz refletido segue o caminho mais curto foi descoberto muito mais tarde por Heron de Alexandria, no século $I~d.C.$.
A demonstração de Heron é simples, porém engenhosa: sejam $A$ e $B$ os mesmos pontos da figura anterior, reproduzidos na figura abaixo, e seja $B~^\prime$ a imagem especular de $B$. A superfície do espelho é o plano bissetor de $BB~^\prime$. O segmento $AB~^\prime$ intercepta o espelho num ponto $P$ e este é o ponto onde o raio de luz é refletido ao passar de $A$ para $B$, pois então $\alpha = \gamma$ e $\gamma = \beta$ e assim $\alpha = \beta$. O percurso total do raio de luz é dado por:
\begin{equation*}
AP + PB = AP + PB~^\prime = AB~^\prime
\end{equation*}
O percurso de $A$ a $B$, passando por qualquer outro ponto $P~^\prime$ do espelho é:
\begin{equation*}
AP~^\prime + P~^\prime B = AP~^\prime + P~^\prime B~^\prime
\end{equation*}
que é maior do que o terceiro lado do triângulo $AP~^\prime B~^\prime$, o lado $AB~^\prime $, o que mostra que o percurso real de $A$ para $B$ do raio de luz refletido no espelho é o menor possível.

[Figura 2]
Temos que deixar claro que estes cálculos só tem sentido se considerarmos que o raio de luz tem todo o percurso em um único meio a uma velocidade constante. No entanto, em meios diferentes, como ar, água, vidro, a luz tem velocidades diferentes. Se um raio de luz passa do ar para a água, ele é refratado passando a uma direção mais próxima da perpendicular à interface. O percurso $APB$ não é mais o caminho mais curto de $A$ a $B$.

[Figura 3]
Em $1621$ o cientista holandês Snell descobriu empiricamente que o caminho real do raio de luz é o que satisfaz a equação:
\begin{equation}
\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \text{constante}
\end{equation}
onde essa constante é independente da posição de $A$ e $B$. Esse fato é chamado de Lei de Refração de Snell. Podemos provar a Lei de Snell partindo do pressuposto de que o raio percorre um caminho de $A$ a $B$ de modo a minimizar o tempo total de percurso.
Seja a velocidade da luz no ar denotada por $V_{ar}$ e na água $V_{ag}$ e seja $T$ o tempo total do percurso, tempo no ar mais o tempo na água:
\begin{equation*}
T = \frac{\sqrt{a^2+x^2}}{V_{ar}} + \frac{\sqrt{b^2+(c-x)^2}}{V_{ag}}\\
\ \\
T = \frac{1}{V_{ar}}\left(a^2+x^2\right)^{1/2} + \frac{1}{V_{ag}}\left(b^2+(c-x)^2\right)^{1/2}
\end{equation*}
Se calcularmos a derivada desta função $T(x)$ e observarmos o seu significado em termos da figura acima, obteremos:
\begin{equation*}
\small \frac{dT}{dx} = \frac{1}{V_{ar}} \cdot \frac{1}{2}\cdot \left(a^2+x^2\right)^{-1/2} \cdot 2x + \frac{1}{V_{ag}}\cdot \frac{1}{2}\cdot \left( b^2+(c-x)^2 \right)^{-1/2} \cdot 2(c-x)\cdot (-1)\\
\end{equation*}
\begin{equation}
\frac{dT}{dx} = \frac{1}{V_{ar}}\cdot\frac{x}{\sqrt{a^2+x^2}} - \frac{1}{V_{ag}}\cdot \frac{c-x}{\sqrt{b^2+(c-x)^2}}
\end{equation}
E ainda pela figura acima, temos:
\begin{equation*}
\text{sen}(\alpha) = \frac{x}{\sqrt{a^2+x^2}} \quad \text{e} \quad \text{sen}(\beta)=\frac{c-x}{\sqrt{b^2(c-x)^2}}
\end{equation*}
Substituindo na derivada anterior, obtemos:
\begin{equation*}
\frac{dT}{dx} = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Para obtermos o $T$ mínimo, igualamos essa derivada a zero:
\begin{equation*}
0 = \frac{\text{sen}(\alpha)}{V_{ar}} - \frac{\text{sen}(\beta)}{V_{ag}}\\
\ \\
\frac{\text{sen}(\alpha)}{V_{ar}} = \frac{\text{sen}(\beta)}{V_{ag}}
\end{equation*}
Ou ainda:
\begin{equation}
\frac{\text{sen}(\alpha)}{\text{sen}(\beta)} = \frac{V_{ar}}{V_{ag}}
\end{equation}
Esta é a forma mais reveladora da Lei de Snell porque dá um significado físico da constante que aparece em $(3)$, pois é a razão entre a velocidade da luz no ar e a velocidade (menor) da luz na água. Essa constante é chamada de índice de refração da água. Se substituírmos a água por qualquer outro meio translúcido, como álcool, glicerina, vidro, ... então a constante teráum valor numérico diferente, pois cada meio possui um índice de refração diferente.
Podemos aplicar o teste da segunda derivada em $(4)$ para verificar se $(5)$ realmente minimiza $T$, observando se esta é positiva:
\begin{equation*}
\frac{d^2T}{dx^2} = \frac{1}{V_{ar}}\frac{a^2}{(a^2+x^2)^{3/2}} + \frac{1}{V_{ag}}\frac{b^2}{\left( b^2+(c-x)^2 \right)^{3/2}}>0
\end{equation*}
Referências:
[1] Cálculo com Geometria Analítica - Simmons - Ed. McGraw-HillVeja mais:
O refinamento de SnellUsando derivadas para aproximar funções
Aplicação de derivadas para determinação de máximos e mínimos

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- O Teorema Da Corda Quebrada De Arquimedes
O matemático árabe Abul Raihan al Biruni atribui a Arquimedes, uma elegante proposição geométrica, chamada teorema da corda quebrada o qual enunciaremos abaixo: Teorema (Arquimedes):Se $AB$ e $BC$ compõem uma corda quebrada $ABC$, onde $BC >...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
