Matemática
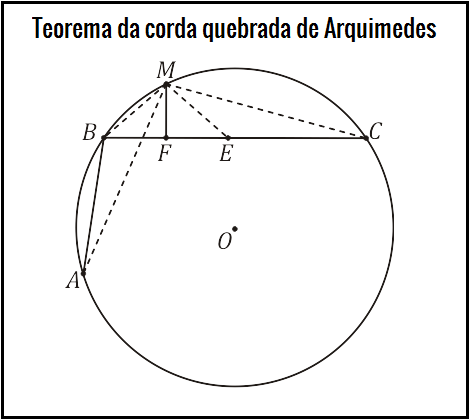
O matemático árabe Abul Raihan al Biruni atribui a Arquimedes, uma elegante proposição geométrica, chamada teorema da corda quebrada o qual enunciaremos abaixo:
\begin{equation*}
AB + BF = FC = \frac{AB+BC}{2}
\end{equation*}
Desde que $AB < BC$ existe um ponto $E$ sobre $BC$ tal que $EC = AB$.
Por hipótese, $M$ é o ponto médio do arco $A\widehat{M}B$, de modo que $AM = MC$, pois cordas de arcos congruentes são congruentes. Além disso, $\hat{A} = \hat{C}$, pois são ângulos de um mesmo arco $\hat{BM}$. Sendo $EC = AB$, segue que $\triangle ABM \simeq \triangle CEM$.
Desta congruência desses triângulos, segue que $BM = ME$ o que prova que o $\triangle MBE$ é isósceles. Sendo $MF$ sua altura, então $\triangle BMF \simeq EMF$, pois $B\hat{F}M = E\hat{F}M = 90^{\circ}$, $MF = MF$ e $BM = ME$. Assim, $BF = FE$, de modo que
\begin{equation*}
AB + BF = EC + FE = FC
\end{equation*}
Logo,
\begin{equation*}
AB + BC = (AB + BF) + FC = 2FC \quad \Rightarrow FC = AB + BF = \frac{AB+BC}{2}
\end{equation*}
\begin{equation}
\sin(\alpha - \beta) = \text{sen} (\alpha) \cos (\beta) - \text{sen} (\beta) \cos (\alpha)
\end{equation}
e
\begin{equation}
\sin(\alpha + \beta) = \text{sen} (\alpha) \cos (\beta) + \text{sen} (\beta) \cos (\alpha)
\end{equation}
Na figura abaixo, $ABC$ é a corda quebrada, $OC = OB = OM = r$.
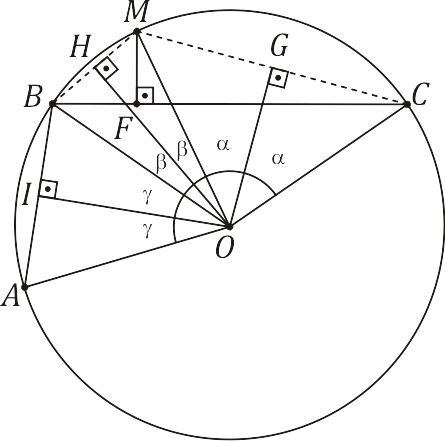
No $\triangle OGM$,
\begin{equation*}
\sin \alpha = \frac{MG}{OR} = \frac{MC/2}{r} \Longrightarrow MC = 2r \text{sen}( \alpha)
\end{equation*}
e no $\triangle OBH$,
No $\triangle CFM$ retângulo em $F$, $M\hat{C}F = B\hat{O}M/2$, ou seja, $M\hat{C}F = \beta$. Assim,
\begin{equation*}
FC = 2r \text{sen} (\alpha) \cos (\beta)
\end{equation*}
Analogamente, no triângulo retângulo $BFM$, temos $M\hat{B}F = M\hat{O}C/2 = \alpha$. Assim
\begin{equation*}
\cos (\alpha) = \frac{BF}{BM} \Longrightarrow BF = 2r \text{sen} (\beta) \cos (\alpha)
\end{equation*}
Pelo teorema da corda quebrada, $AB + BF = FC$, de modo que
\begin{equation*}
AB = FC - BF \Longrightarrow AB = 2r(\text{sen} (\alpha) \cos (\beta) - \text{sen}(\beta) \cos (\alpha))
\end{equation*}
No $\triangle BOI$ retângulo em $I$,
\begin{equation*}
\text{sen} (\gamma) = \frac{BI}{OB} = \frac{AB/2}{r} \Longrightarrow AB = 2r \text{sen} (\gamma)
\end{equation*}
Mas o arco $\widehat{AM} = \widehat{MC}$, donde segue que $2\gamma + 2\beta = 2\alpha \Longrightarrow \gamma = \alpha - \beta$. Logo:
\begin{equation*}
AB = 2r \text{sen}(\alpha - \beta) \Rightarrow 2r \text{sen}(\alpha - \beta) = 2r(\text{sen} (\alpha) \cos (\beta) - \text{sen} (\beta) \cos (\alpha))
\end{equation*}
donde segue a identidade $(1)$.
Para provar a identidade $(2)$, sabemos do teorema da corda quebrada que $BF + FC = BC$ e que o arco $\widehat{BC} = 2\alpha + 2\beta = 2(\alpha + \beta)$ . Assim,
\begin{equation*}
\text{sen}(\alpha + \beta) = \text{sen}\left(\frac{\widehat{BC}}{2}\right) = \frac{BC/2}{r} \Longrightarrow BC = 2r \text{sen}(\alpha + \beta)
\end{equation*}
Logo,
\begin{equation*}
2r \text{sen}(\alpha + \beta) = BC = BF + FC = 2r \text{sen}(\alpha) \cos (\beta) + 2r \text{sen} (\beta) \cos (\alpha)
\end{equation*}
donde segue a demonstração.
*Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
O corpus arquimediano
Teorema do ângulo inscrito

- Aplicação De Derivadas No Estudo Sobre A Reflexão E Refração De Um Raio De Luz
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível. Considere um raio de luz que parte de um ponto...
- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Teorema Do Quadrilátero Inscritível
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência. Teorema: Se um quadrilátero é inscritível numa circunferência, então os ângulos opostos são suplementares. Por hipóteses temos que o quadrilátero...
- Soma Dos Ângulos Internos E Externos De Um Polígono Convexo
A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$. Ângulos Internos Definição $1$: Ângulo interno...
Matemática
O teorema da corda quebrada de Arquimedes
O matemático árabe Abul Raihan al Biruni atribui a Arquimedes, uma elegante proposição geométrica, chamada teorema da corda quebrada o qual enunciaremos abaixo:

Teorema (Arquimedes):
Se $AB$ e $BC$ compõem uma corda quebrada $ABC$, onde $BC > AB$ e se $M$ é o ponto médio do arco $A\widehat{B}C$, então o pé $F$ da perpendicular de $M$ sobre $BC$ é o ponto médio da corda quebrada.Demonstração:
Na figura acima, provaremos que:\begin{equation*}
AB + BF = FC = \frac{AB+BC}{2}
\end{equation*}
Desde que $AB < BC$ existe um ponto $E$ sobre $BC$ tal que $EC = AB$.
Por hipótese, $M$ é o ponto médio do arco $A\widehat{M}B$, de modo que $AM = MC$, pois cordas de arcos congruentes são congruentes. Além disso, $\hat{A} = \hat{C}$, pois são ângulos de um mesmo arco $\hat{BM}$. Sendo $EC = AB$, segue que $\triangle ABM \simeq \triangle CEM$.
Desta congruência desses triângulos, segue que $BM = ME$ o que prova que o $\triangle MBE$ é isósceles. Sendo $MF$ sua altura, então $\triangle BMF \simeq EMF$, pois $B\hat{F}M = E\hat{F}M = 90^{\circ}$, $MF = MF$ e $BM = ME$. Assim, $BF = FE$, de modo que
\begin{equation*}
AB + BF = EC + FE = FC
\end{equation*}
Logo,
\begin{equation*}
AB + BC = (AB + BF) + FC = 2FC \quad \Rightarrow FC = AB + BF = \frac{AB+BC}{2}
\end{equation*}
Consequência:
Se o arco $\widehat{MC} = 2\alpha$ e o arco $\widehat{BM} = 2\beta$, então\begin{equation}
\sin(\alpha - \beta) = \text{sen} (\alpha) \cos (\beta) - \text{sen} (\beta) \cos (\alpha)
\end{equation}
e
\begin{equation}
\sin(\alpha + \beta) = \text{sen} (\alpha) \cos (\beta) + \text{sen} (\beta) \cos (\alpha)
\end{equation}
Na figura abaixo, $ABC$ é a corda quebrada, $OC = OB = OM = r$.

No $\triangle OGM$,
\begin{equation*}
\sin \alpha = \frac{MG}{OR} = \frac{MC/2}{r} \Longrightarrow MC = 2r \text{sen}( \alpha)
\end{equation*}
e no $\triangle OBH$,
No $\triangle CFM$ retângulo em $F$, $M\hat{C}F = B\hat{O}M/2$, ou seja, $M\hat{C}F = \beta$. Assim,
\begin{equation*}
FC = 2r \text{sen} (\alpha) \cos (\beta)
\end{equation*}
Analogamente, no triângulo retângulo $BFM$, temos $M\hat{B}F = M\hat{O}C/2 = \alpha$. Assim
\begin{equation*}
\cos (\alpha) = \frac{BF}{BM} \Longrightarrow BF = 2r \text{sen} (\beta) \cos (\alpha)
\end{equation*}
Pelo teorema da corda quebrada, $AB + BF = FC$, de modo que
\begin{equation*}
AB = FC - BF \Longrightarrow AB = 2r(\text{sen} (\alpha) \cos (\beta) - \text{sen}(\beta) \cos (\alpha))
\end{equation*}
No $\triangle BOI$ retângulo em $I$,
\begin{equation*}
\text{sen} (\gamma) = \frac{BI}{OB} = \frac{AB/2}{r} \Longrightarrow AB = 2r \text{sen} (\gamma)
\end{equation*}
Mas o arco $\widehat{AM} = \widehat{MC}$, donde segue que $2\gamma + 2\beta = 2\alpha \Longrightarrow \gamma = \alpha - \beta$. Logo:
\begin{equation*}
AB = 2r \text{sen}(\alpha - \beta) \Rightarrow 2r \text{sen}(\alpha - \beta) = 2r(\text{sen} (\alpha) \cos (\beta) - \text{sen} (\beta) \cos (\alpha))
\end{equation*}
donde segue a identidade $(1)$.
Para provar a identidade $(2)$, sabemos do teorema da corda quebrada que $BF + FC = BC$ e que o arco $\widehat{BC} = 2\alpha + 2\beta = 2(\alpha + \beta)$ . Assim,
\begin{equation*}
\text{sen}(\alpha + \beta) = \text{sen}\left(\frac{\widehat{BC}}{2}\right) = \frac{BC/2}{r} \Longrightarrow BC = 2r \text{sen}(\alpha + \beta)
\end{equation*}
Logo,
\begin{equation*}
2r \text{sen}(\alpha + \beta) = BC = BF + FC = 2r \text{sen}(\alpha) \cos (\beta) + 2r \text{sen} (\beta) \cos (\alpha)
\end{equation*}
donde segue a demonstração.
*Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Referências:
[1] O teorema da corda quebrada de Arquimedes no blog Fatos MatemáticosVeja mais:
O cálculo no JapãoO corpus arquimediano
Teorema do ângulo inscrito

- Aplicação De Derivadas No Estudo Sobre A Reflexão E Refração De Um Raio De Luz
Utilizando derivadas como forma de otimização, vamos aplicar no problema de reflexão da luz em um espelho plano e da refração da luz na água, demonstrando que a luz percorre o menor caminho possível. Considere um raio de luz que parte de um ponto...
- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Teorema Do Quadrilátero Inscritível
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência. Teorema: Se um quadrilátero é inscritível numa circunferência, então os ângulos opostos são suplementares. Por hipóteses temos que o quadrilátero...
- Soma Dos Ângulos Internos E Externos De Um Polígono Convexo
A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$. Ângulos Internos Definição $1$: Ângulo interno...
