Matemática

Soma dos Ângulos Internos e Externos de um Polígono Convexo

A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$.

Ângulos Internos

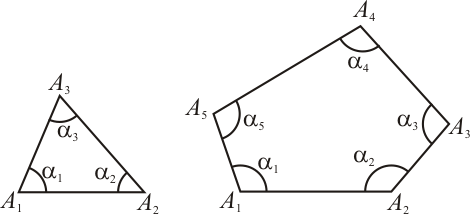
Definição $1$: Ângulo interno de um polígono é o ângulo formado por dois de seus lados, que seja interno ao polígono.

[Figura 1]

Teorema $1$: A soma das medidas dos ângulos internos de um polígono convexo de $N$ lados é dada pela fórmula:

\begin{equation}
S_\alpha = (N-2)\cdot 180^\circ
\end{equation}
onde:

$\bullet$ $S_\alpha$ é a soma dos ângulos internos;
$\bullet$ $N$ é o número de lados do polígono.

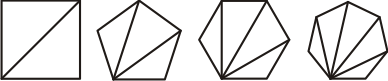
Demonstração: Tomando um polígono convexo, para $N>3$, podemos decompô-lo em triângulos, traçando diagonais a partir de um vértice qualquer:

[Figura 2]

Vejam que há uma relação entre o número de lados do polígono e a quantidade de triângulos em que podemos decompô-lo:

[Tabela 1]

Como soma das medidas dos ângulo internos de um polígono é igual à soma das medidas dos ângulos internos de todos os $N-2$ triângulos que o compõe, e como a soma das medidas dos ângulos internos de cada triângulo é igual a $180^\circ$, temos:

\begin{equation}
S_\alpha = (N-2) \cdot 180^\circ
\end{equation}

Uma consequência direta desse resultado é a determinação do ângulo interno de um polígono regular, dado por:

\begin{equation}
\alpha = \frac{(N-2)\cdot 180^\circ}{N}
\end{equation}

onde $\alpha$ é a medida de cada ângulo interno de um polígono regular de $N$ lados.

Ângulos Externos

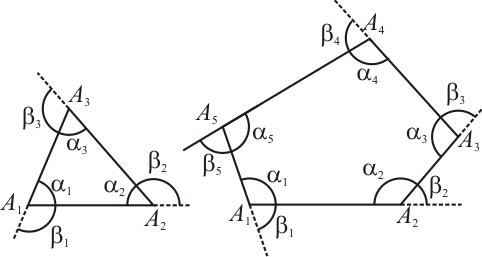
Definição $2$: Ângulo externo de um polígono é aquele suplementar ao ângulo interno em um dado vértice, formado pelo prolongamento de um dos lados e o lado adjacente.

[Figura 3]

Teorema $2$: A soma das medidas dos ângulos externos de um polígono convexo de $N$ lados é igual a $360^\circ$:

\begin{equation}
S_\beta = \beta_1, \beta_2, \beta_3, \cdots, \beta_N=360^\circ
\end{equation}
onde:

$\bullet$ $\beta_N$ é o ângulo externo do polígono;
$\bullet$ $S_\beta$ é a soma dos ângulos externos.

Demonstração: Partimos do fato que a soma dos ângulos interno e externo é igual a um ângulo raso. Assim:

\begin{equation}
\alpha + \beta = 180^\circ
\end{equation}

Então, para cada par de ângulos associados a um lado $N$ do polígono, temos:

\begin{equation}
\begin{matrix}
\alpha_1 + \beta_1 = 180^\circ\\
\alpha_2 + \beta_2 = 180^\circ\\
\alpha_3 + \beta_3 = 180^\circ\\
\vdots \\
\alpha_N + \beta_N = 180^\circ\\
\end{matrix}
\end{equation}

Somando membro a membro as $N$ igualdades, obtemos:

\begin{equation}
S_\alpha + S_\beta = N \cdot 180^\circ
\end{equation}
onde:

$\bullet$ $S_\alpha$ é a soma dos ângulos internos;

$\bullet$ $S_\beta$ é a soma dos ângulos externos;

$\bullet$ $N$ é o número de lados do polígono.

Manipulando a equação $(7)$, obtemos:

\begin{equation}
S_\beta = N \cdot 180^\circ - S_\alpha
\end{equation}

Substituindo $S_\alpha$ dada na equação $(2)$, obtemos:

\begin{equation}
\begin{matrix}
S_\beta = N\cdot 180^\circ - (N-2) \cdot 180^\circ\\
S_\beta = N\cdot 180^\circ - N\cdot 180^\circ + 360^\circ\\
S_\beta = 360^\circ
\end{matrix}
\end{equation}

Uma consequência imediata desse resultado é a determinação da medida de um ângulo externo de um polígono regular, dada por:

\begin{equation}
\beta = \frac{S_\beta}{N} \qquad \text{ou} \qquad \beta = \frac{360^\circ}{N}
\end{equation}
onde $\beta$ é a medida de cada ângulo externo de um polígono regular de $N$ lados.

Exemplo $1$: Calcular a soma das medidas dos ângulos internos de um heptágono.

Temos que $N=7$, já que o polígono é um heptágono. Assim:

\begin{matrix}
S_\alpha=(N-2)\cdot 180^\circ \\
S_\alpha= (7-2)\cdot 180^\circ\\
S_\alpha= 5\cdot 180^\circ\\
S_\alpha = 900^\circ
\end{matrix}

Desse modo, a soma dos ângulos internos de um heptágono vale $900^\circ$.

Exemplo $2$: Calcular a soma das medidas dos ângulos internos de um eneágono regular e determinar a medida de cada ângulo externo.

Temos que $N=9$. Fazemos:

\begin{matrix}
S_\alpha = (N-2)\cdot 180^\circ\\
S_\alpha = (9-2) \cdot 180^\circ\\
S_\alpha = 7 \cdot 180^\circ\\
S_\alpha = 1260^\circ
\end{matrix}

Para sabermos quanto vale cada ângulo interno, dividimos a soma dos ângulos internos por $9$, obtendo $140^\circ$. Agora, para calcularmos o ângulo externo, basta fazermos:

\begin{matrix}
\beta = 180^\circ - \alpha\\
\beta = 180^\circ - 140^\circ\\
\beta = 40^\circ
\end{matrix}

Exemplo $3$: Qual polígono possui a soma das medidas dos ângulos internos igual a $1800^\circ$?

Basta aplicarmos a fórmula:
\begin{matrix}
S_\alpha = (N-2) \cdot 180^\circ\\
1800^\cdot = 180^\circ \cdot N - 360^\circ\\
180^\circ \cdot N = 2160^\circ\\
N = 12
\end{matrix}

Logo, o polígono procurado é o dodecágono.

Exemplo $4$: Qual polígono regular possui a medida dos ângulos externos igual a $60^\circ$?

Aplicamos a fórmula dada em $(10)$:

\begin{matrix}
\beta = \frac{360^\circ}{N}\\
N = \frac{360^\circ}{60}=6
\end{matrix}

Logo, o polígono em questão é um hexágono.

Exemplo $5$: Qual é o polígono regular cuja medida do ângulo interno é o triplo da medida do ângulo externo?

Podemos escrever que $\alpha = 3\beta$. E agora substituirmos as equações $(3)$ e $(10)$:

\begin{matrix}
\frac{(N-2)\cdot 180^\circ}{N} = 3\cdot \frac{360^\circ}{N}\\
180^\circ \cdot N - 360^\circ = 1080^\circ\\
180^\circ \cdot N = 1440^\circ\\
N=8
\end{matrix}

Referências:

$[1]$ Fundamentos de Matemática $7^a$ - Ismael Reis - Ed. Moderna

Veja mais:

O Ângulo Interno de um Polígono Regular
Teorema do Ângulo Inscrito
A Soma dos Ângulos Internos de um Triângulo no blog Fatos Matemáticos

- Um Problema Famoso De Geometria
Olá gente! Hoje aprensentarei um problema bastante conhecido em geometria e algumas de suas soluções também muito conhecidas. O triângulo ao lado é isósceles de vértice . Sendo e calcule . Resolução 1 : Vamos usar lei dos senos...

- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....

- O Teorema Da Corda Quebrada De Arquimedes
O matemático árabe Abul Raihan al Biruni atribui a Arquimedes, uma elegante proposição geométrica, chamada teorema da corda quebrada o qual enunciaremos abaixo: Teorema (Arquimedes):Se $AB$ e $BC$ compõem uma corda quebrada $ABC$, onde $BC >...

- Os Pontos De Brocard (parte 2)
Na primeira postagem desta série, vimos as definições dos Pontos de Brocard e suas construções geométricas. Nesta postagem, veremos algumas propriedades importantes, teorema, corolários e suas respectivas demonstrações. Por: Kleber KilhianPaulo...

- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...

Matemática