Matemática
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo.
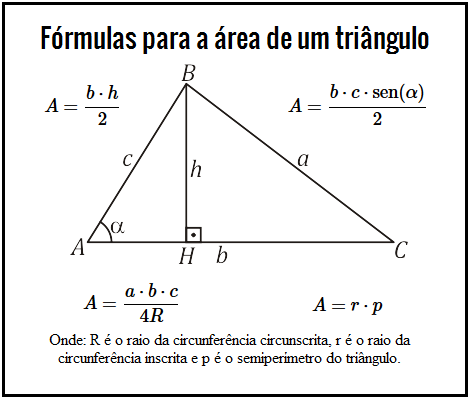
Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes.
Seja o paralelogramo $ABDC$ representado pela figura abaixo, onde $b$ e $h$ são as medidas da base e da altura, respectivamente.
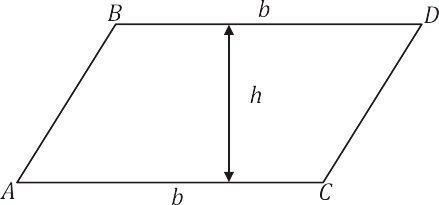
Projetando os pontos $B$ e $D$ sobre a reta $\overleftrightarrow{AC}$, obtemos os pontos $P$ e $Q$, determinando o retângulo $PBDQ$:
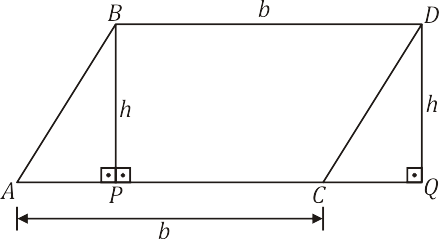
Note que os triângulos $APB$ e $CQD$ são congruentes e suas áreas são iguais. Assim, a área do paralelogramo $ABDC$ é igual à área do retângulo $PBDQ$ e é dada pelo produto da base pela altura:
\begin{equation}
A = b \cdot h
\end{equation}
Agora, tomemos um triângulo $ABC$, cuja base $\overline{AC}$ mede $b$ e sua altura relativa à esta base me $h$:
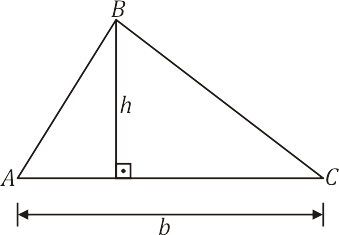
Se traçarmos as respectivas paralelas aos lados $\overline{AC}$ e $\overline{AB}$ a partir de $B$ e $C$, estas interceptam-se no ponto $D$, determinando o paralelogramo $ABDC$, onde $b$ e $h$ são as medidas da base e altura, respectivamente.
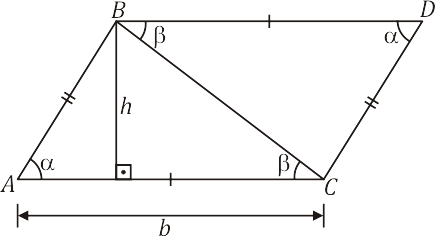
Como $AB=CD$, $m(B\hat{A}C) = m(B\hat{D}C)=\alpha$ e $AC=BD$, os triângulos $ABC$ e $DCB$ são congruentes e, portanto, suas áreas são iguais. Logo, a área do triângulo $ABC$ é igual à metade da área do paralelogramo $ABD$, ou seja:
\begin{equation}
A = \frac{b \cdot h}{2}
\end{equation}
Do triângulo $AHB$, temos que:
\begin{equation}
\text{sen}(\alpha) = \frac{h}{c}
\end{equation}
Substituindo $(3)$ na relação $(2)$, obteremos que a área do triângulo $ABC$ será dada por:
\begin{equation}
A = \frac{b \cdot c \cdot \text{sen}(\alpha)}{2}
\end{equation}
Analogamente obtemos:
\begin{equation}
A=\frac{a \cdot c \cdot \text{sen}(\beta)}{2} \qquad \text{e} \qquad A=\frac{a \cdot b \cdot \text{sen}(\gamma)}{2}
\end{equation}
Como a circunferência é inscrita ao triângulo $ABC$, os segmentos $\overline{OP}$, $\overline{OQ}$ e $\overline{OR}$ são as respectivas alturas dos triângulos $AOB$, $BOC$ e $AOC$ e medem $r$.
A área do triângulo $ABC$ é a soma das áreas $A_1$, $A_s$ e $A_3$ dos triângulos $AOB$, $BOC$ e $AOC$, respectivamente.
\begin{equation*}
A = A_1 + A_2 + A_3
\end{equation*}
Utilizando a relação $(2)$, obtemos:
\begin{equation}
A = \frac{c \cdot r}{2} + \frac{a \cdot r}{2} + \frac{b \cdot r}{2}\\
\ \\
A = \frac{r(a+b+c)}{2}
\end{equation}
No entanto, o semiperímetro $p$ do triângulo é dado por:
\begin{equation}
p = \frac{a+b+c}{2}
\end{equation}
Substituindo $(7)$ em $(6)$, obtemos:
\begin{equation}
A = r \cdot p
\end{equation}
Considerando a relação $(2)$, podemos escrever a área do triângulo $ABC$ como:
\begin{equation}
A = \frac{b \cdot h}{2}
\end{equation}
Para calcularmos a medida da altura $h$, construímos o triângulo $BCD$, onde $\overline{BD}=2R$. Assim:
\begin{equation*}
m(B \hat{H} A) = m(B \hat{C} D) = 90^\circ
\end{equation*}
Como os ângulos $\alpha$ são inscritos na circunferência e possuem o mesmo correspondente ângulo central $B\hat{O}C$, então:
\begin{equation*}
m(B\hat{A}C) = m(B\hat{D}C) = \frac{m(B\hat{O}C)}{2}
\end{equation*}
Como $\triangle AHB \sim \triangle BCD$, logo:
\begin{equation}
\frac{BH}{BC} = \frac{AB}{BD} \Longrightarrow \frac{h}{a} = \frac{c}{2R} \Longrightarrow h = \frac{a\cdot c}{2R}
\end{equation}
Substituindo $(10)$ em $(9)$, obtemos:
\begin{equation}
A = \frac{a\cdot b \cdot c}{4R}
\end{equation}
Usaremos a fórmula dada em $(4)$:
\begin{equation*}
A = \frac{a \cdot b \cdot \text{sen}(\alpha)}{2}\\
\ \\
A = \frac{12 \cdot 18 \cdot \text{sen}(30^\circ)}{2}\\
\ \\
A = \frac{12 \cdot 18}{4}\\
\ \\
A = 54\ cm^2
\end{equation*}
Seja $x$ a medida do terceiro lado. Usemos a fórmula dada em $(8)$:
\begin{equation*}
A = r\cdot p
\end{equation*}
O semiperímetro $p$ do triângulo é dado por:
\begin{equation*}
p = \frac{x + 15 + 21}{2} = \frac{x + 36}{2}
\end{equation*}
Substituindo $p$, a área $A$ e o raio $r$ da circunferência inscrita, na relação anterior, obtemos:
\begin{equation*}
180 = 6\cdot \frac{x+36}{2}\\
\ \\
x = 24\ cm
\end{equation*}
Como temos as medidas dos lados e do raio da circunferência circunscrita ao triângulo, aplicams a fórmula dada em $(11)$:
\begin{equation*}
A = \frac{a\cdot b\cdot c}{4R}\\
\ \\
A = \frac{4\sqrt{2} \cdot 4 \sqrt{3} \cdot 2(\sqrt{6}+\sqrt{2})}{16}\\
\ \\
A = 2(\sqrt{2} \cdot \sqrt{3} \cdot (\sqrt{6}+\sqrt{2})\\
\ \\
A = 2(\sqrt{6} \cdot \sqrt{6} + \sqrt{6}\cdot \sqrt{2})\\
\ \\
A = 2(6+\sqrt{12})\\
\ \\
A = 12+4\sqrt{3}\\
\ \\
A \approx 18,93\ cm^2
\end{equation*}
Pontos notáveis de um triângulo
O teorema de Pitágoras, segundo Euclides

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Fórmulas para a área de um triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo.

Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes.
Seja o paralelogramo $ABDC$ representado pela figura abaixo, onde $b$ e $h$ são as medidas da base e da altura, respectivamente.

Projetando os pontos $B$ e $D$ sobre a reta $\overleftrightarrow{AC}$, obtemos os pontos $P$ e $Q$, determinando o retângulo $PBDQ$:

Note que os triângulos $APB$ e $CQD$ são congruentes e suas áreas são iguais. Assim, a área do paralelogramo $ABDC$ é igual à área do retângulo $PBDQ$ e é dada pelo produto da base pela altura:
\begin{equation}
A = b \cdot h
\end{equation}
Agora, tomemos um triângulo $ABC$, cuja base $\overline{AC}$ mede $b$ e sua altura relativa à esta base me $h$:

Se traçarmos as respectivas paralelas aos lados $\overline{AC}$ e $\overline{AB}$ a partir de $B$ e $C$, estas interceptam-se no ponto $D$, determinando o paralelogramo $ABDC$, onde $b$ e $h$ são as medidas da base e altura, respectivamente.

Como $AB=CD$, $m(B\hat{A}C) = m(B\hat{D}C)=\alpha$ e $AC=BD$, os triângulos $ABC$ e $DCB$ são congruentes e, portanto, suas áreas são iguais. Logo, a área do triângulo $ABC$ é igual à metade da área do paralelogramo $ABD$, ou seja:
\begin{equation}
A = \frac{b \cdot h}{2}
\end{equation}
Área de um triângulo em função de dois lados e do seno do ângulo compreendido entre eles
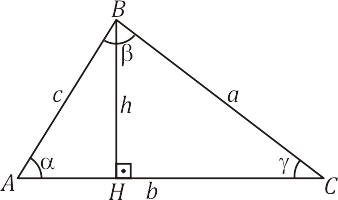
Seja o triângulo $ABC$, representado na figura $6$, onde $\alpha$ é o ângulo interno do vértice $A$, $h$ é a altura relativa ao lado $\overline{AC}$ e $c$ é o lado oposto ao vértice $C$.
Do triângulo $AHB$, temos que:
\begin{equation}
\text{sen}(\alpha) = \frac{h}{c}
\end{equation}
Substituindo $(3)$ na relação $(2)$, obteremos que a área do triângulo $ABC$ será dada por:
\begin{equation}
A = \frac{b \cdot c \cdot \text{sen}(\alpha)}{2}
\end{equation}
Analogamente obtemos:
\begin{equation}
A=\frac{a \cdot c \cdot \text{sen}(\beta)}{2} \qquad \text{e} \qquad A=\frac{a \cdot b \cdot \text{sen}(\gamma)}{2}
\end{equation}
Área de um triângulo em função das medidas de seus lados e da medida do raio da circunferência inscrita
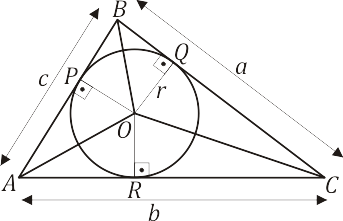
Seja o triângulo $ABC$, representado na figura abaixo, onde $a$, $b$ e $c$ são as respectivas medidas dos lados opostos aos vértices $A$, $B$ e $C$ e seja $r$ a medida do raio da circunferência de centro $O$, inscrita nesse triângulo.
Como a circunferência é inscrita ao triângulo $ABC$, os segmentos $\overline{OP}$, $\overline{OQ}$ e $\overline{OR}$ são as respectivas alturas dos triângulos $AOB$, $BOC$ e $AOC$ e medem $r$.
A área do triângulo $ABC$ é a soma das áreas $A_1$, $A_s$ e $A_3$ dos triângulos $AOB$, $BOC$ e $AOC$, respectivamente.
\begin{equation*}
A = A_1 + A_2 + A_3
\end{equation*}
Utilizando a relação $(2)$, obtemos:
\begin{equation}
A = \frac{c \cdot r}{2} + \frac{a \cdot r}{2} + \frac{b \cdot r}{2}\\
\ \\
A = \frac{r(a+b+c)}{2}
\end{equation}
No entanto, o semiperímetro $p$ do triângulo é dado por:
\begin{equation}
p = \frac{a+b+c}{2}
\end{equation}
Substituindo $(7)$ em $(6)$, obtemos:
\begin{equation}
A = r \cdot p
\end{equation}
Área de um triângulo em função das medidas dos lados e da medida do raio da circunferência circunscrita
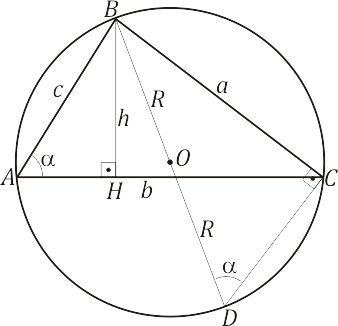
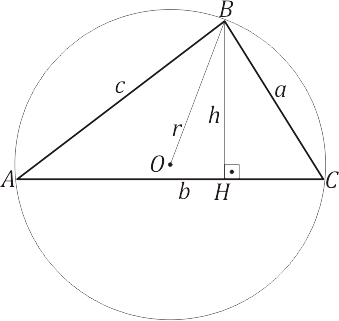
Seja o triângulo $ABC$ inscrito à circunferência de centro $O$ e raio $R$, conforme representa a imagem abaixo:
Considerando a relação $(2)$, podemos escrever a área do triângulo $ABC$ como:
\begin{equation}
A = \frac{b \cdot h}{2}
\end{equation}
Para calcularmos a medida da altura $h$, construímos o triângulo $BCD$, onde $\overline{BD}=2R$. Assim:
\begin{equation*}
m(B \hat{H} A) = m(B \hat{C} D) = 90^\circ
\end{equation*}
Como os ângulos $\alpha$ são inscritos na circunferência e possuem o mesmo correspondente ângulo central $B\hat{O}C$, então:
\begin{equation*}
m(B\hat{A}C) = m(B\hat{D}C) = \frac{m(B\hat{O}C)}{2}
\end{equation*}
Como $\triangle AHB \sim \triangle BCD$, logo:
\begin{equation}
\frac{BH}{BC} = \frac{AB}{BD} \Longrightarrow \frac{h}{a} = \frac{c}{2R} \Longrightarrow h = \frac{a\cdot c}{2R}
\end{equation}
Substituindo $(10)$ em $(9)$, obtemos:
\begin{equation}
A = \frac{a\cdot b \cdot c}{4R}
\end{equation}
Exemplo $1$:
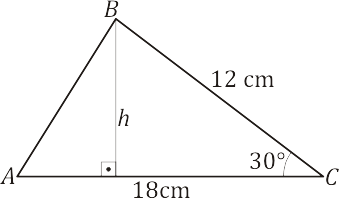
Dado um triângulo $ABC$, onde $\overline{BC} = 12\ cm$, $\overline{AC}=18\ cm$ e $m(A\hat{C}B)=30^\circ$, determinar a sua área.
Usaremos a fórmula dada em $(4)$:
\begin{equation*}
A = \frac{a \cdot b \cdot \text{sen}(\alpha)}{2}\\
\ \\
A = \frac{12 \cdot 18 \cdot \text{sen}(30^\circ)}{2}\\
\ \\
A = \frac{12 \cdot 18}{4}\\
\ \\
A = 54\ cm^2
\end{equation*}
Exemplo $2$:
A área de um triângulo $ABC$ é igual a $180\ cm^2$ e dois de seus lados medem $15\ cm$ e $21\ cm$. Determinar a medida do terceiro lado desse triângulo, sabendo que a medida do raio da circunferência inscrita a ele é de $6\ cm$.Seja $x$ a medida do terceiro lado. Usemos a fórmula dada em $(8)$:
\begin{equation*}
A = r\cdot p
\end{equation*}
O semiperímetro $p$ do triângulo é dado por:
\begin{equation*}
p = \frac{x + 15 + 21}{2} = \frac{x + 36}{2}
\end{equation*}
Substituindo $p$, a área $A$ e o raio $r$ da circunferência inscrita, na relação anterior, obtemos:
\begin{equation*}
180 = 6\cdot \frac{x+36}{2}\\
\ \\
x = 24\ cm
\end{equation*}
Exemplo $3$:
Dado um triângulo $ABC$ inscrito a uma circunferência de centro $O$ e raio $R=4\ cm$, cujas medidas de seus lados medem $a=4\sqrt{2}\ cm$, $b=2(\sqrt{6}+\sqrt{2})$e $c=4\sqrt{3}$. Determinar a área do triângulo $ABC$.
Como temos as medidas dos lados e do raio da circunferência circunscrita ao triângulo, aplicams a fórmula dada em $(11)$:
\begin{equation*}
A = \frac{a\cdot b\cdot c}{4R}\\
\ \\
A = \frac{4\sqrt{2} \cdot 4 \sqrt{3} \cdot 2(\sqrt{6}+\sqrt{2})}{16}\\
\ \\
A = 2(\sqrt{2} \cdot \sqrt{3} \cdot (\sqrt{6}+\sqrt{2})\\
\ \\
A = 2(\sqrt{6} \cdot \sqrt{6} + \sqrt{6}\cdot \sqrt{2})\\
\ \\
A = 2(6+\sqrt{12})\\
\ \\
A = 12+4\sqrt{3}\\
\ \\
A \approx 18,93\ cm^2
\end{equation*}
Referências:
[1] Matemática - Ciência e Aplicações - V2 - Gelson Iezzi et al. - Ed. SaraivaVeja mais:
Teorema do ângulo inscritoPontos notáveis de um triângulo
O teorema de Pitágoras, segundo Euclides

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
