Matemática
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante.
\begin{equation*}
\frac{AE}{AC} = \frac{AB}{AD} = \frac{BE}{DC}
\end{equation*}
de modo que
\begin{equation}
EB = \frac{AB\cdot DC}{AD}
\end{equation}
Além disso, sendo $\triangle ACD \sim \triangle AEB$, então $E\hat{A}C = B\hat{A}D$ e sendo $\displaystyle \frac{AD}{AC} = \frac{AB}{AE}$ segue que $\triangle EAC \sim \triangle BAD$.
Assim,
\begin{equation}
\frac{EC}{AC} = \frac{BD}{AD} \quad \Longrightarrow \quad EC = \frac{AC\cdot BD}{AD}
\end{equation}
Agora se $ABCD$ é um quadrilátero cíclico, temos
\begin{equation*}
A\hat{B}E + C\hat{B}A = A\hat{D}C + C\hat{B}A = 180^{\circ}
\end{equation*}
Isto significa que os pontos $C$, $B$ e $E$ são colineares e portanto,
\begin{equation}
EC = EB + BC
\end{equation}
Substituindo $(1)$ e $(2)$ em $(3)$, temos
\begin{equation*}
\frac{AC\cdot BD}{AD} = \frac{AB\cdot DC}{AD} + BC
\end{equation*}
de modo que
\begin{equation}
AC\cdot BD = AB\cdot CD + BC\cdot AD
\end{equation}
A expressão $(4)$ é conhecida por igualdade de Ptolomeu. Se o quadrilátero $ABCD$ não é cíclico, então
\begin{equation*}
A\hat{B}E + C\hat{B}A = A\hat{D}C + C\hat{B}A \neq 180^{\circ}
\end{equation*}
de modo que os pontos $C$, $B$ e $E$ formam um triângulo e pela desigualdade triangular segue que
\begin{equation}
EC < EB + BC
\end{equation}
Substituindo $(1)$ e $(2)$ em $(5)$, temos:
\begin{equation*}
\frac{AC\cdot BD}{AD} < \frac{AB\cdot DC}{AD} + BC
\end{equation*}
e então:
\begin{equation}
AC\cdot BD < AB\cdot CD + BC\cdot AD
\end{equation}
De $(4)$ e $(6)$, obtemos a desigualdade de Ptolomeu, ou seja,
\begin{equation*}
AC\cdot BD \leq AB\cdot CD + BC\cdot AD
\end{equation*}
e a igualdade é válida se, e somente se, $ABCD$ é cíclico.
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
A Astronomia e os astrônomos da Grécia Antiga
Teste da integral para convergência de séries

- Resolução Da Integral $\int \frac{1}{a-bx}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a-bx}dx = -\frac{\ln(a-bx)}{b}+C \end{equation*} onde $a$ e $b$ são constantes tais que $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq bx$ e $b \neq 0$. Seja a integral: \begin{equation*}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
Matemática
A desigualdade de Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante.

Proposição 1
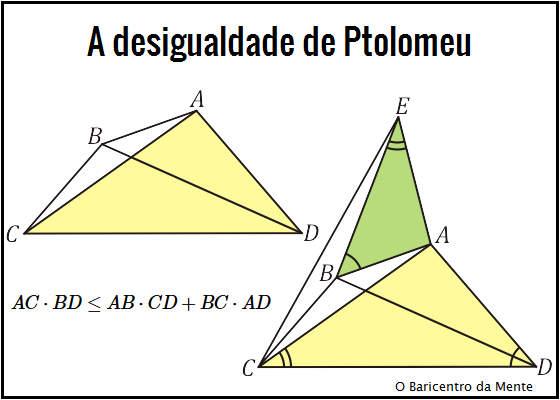
Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais, então $AC\cdot BD \leq AB\cdot CD + BC\cdot AD$ e a igualdade é válida se e somente se $ABCD$ é um quadrilátero cíclico.Demonstração
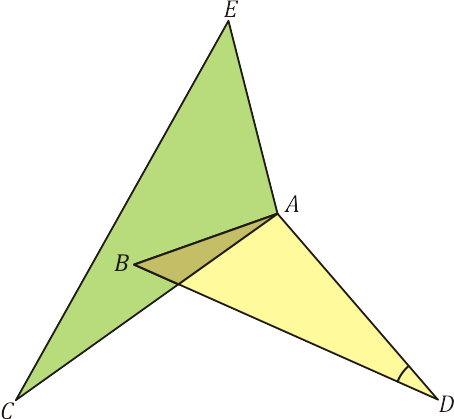
No quadrilátero $ABCD$ acima, seja $E$ um ponto tal que os triângulos $ACD$ e $AEB$ sejam semelhantes. $(A\hat{E}B = A\hat{C}D)$ e $(B\hat{A}E = C\hat{A}D)$. Assim,\begin{equation*}
\frac{AE}{AC} = \frac{AB}{AD} = \frac{BE}{DC}
\end{equation*}
de modo que
\begin{equation}
EB = \frac{AB\cdot DC}{AD}
\end{equation}
Além disso, sendo $\triangle ACD \sim \triangle AEB$, então $E\hat{A}C = B\hat{A}D$ e sendo $\displaystyle \frac{AD}{AC} = \frac{AB}{AE}$ segue que $\triangle EAC \sim \triangle BAD$.
Assim,
\begin{equation}
\frac{EC}{AC} = \frac{BD}{AD} \quad \Longrightarrow \quad EC = \frac{AC\cdot BD}{AD}
\end{equation}
Agora se $ABCD$ é um quadrilátero cíclico, temos
\begin{equation*}
A\hat{B}E + C\hat{B}A = A\hat{D}C + C\hat{B}A = 180^{\circ}
\end{equation*}
Isto significa que os pontos $C$, $B$ e $E$ são colineares e portanto,
\begin{equation}
EC = EB + BC
\end{equation}
Substituindo $(1)$ e $(2)$ em $(3)$, temos
\begin{equation*}
\frac{AC\cdot BD}{AD} = \frac{AB\cdot DC}{AD} + BC
\end{equation*}
de modo que
\begin{equation}
AC\cdot BD = AB\cdot CD + BC\cdot AD
\end{equation}
A expressão $(4)$ é conhecida por igualdade de Ptolomeu. Se o quadrilátero $ABCD$ não é cíclico, então
\begin{equation*}
A\hat{B}E + C\hat{B}A = A\hat{D}C + C\hat{B}A \neq 180^{\circ}
\end{equation*}
de modo que os pontos $C$, $B$ e $E$ formam um triângulo e pela desigualdade triangular segue que
\begin{equation}
EC < EB + BC
\end{equation}
Substituindo $(1)$ e $(2)$ em $(5)$, temos:
\begin{equation*}
\frac{AC\cdot BD}{AD} < \frac{AB\cdot DC}{AD} + BC
\end{equation*}
e então:
\begin{equation}
AC\cdot BD < AB\cdot CD + BC\cdot AD
\end{equation}
De $(4)$ e $(6)$, obtemos a desigualdade de Ptolomeu, ou seja,
\begin{equation*}
AC\cdot BD \leq AB\cdot CD + BC\cdot AD
\end{equation*}
e a igualdade é válida se, e somente se, $ABCD$ é cíclico.
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Referências:
[1] A desigualdade de Ptolomeu no blog Fatos Matemáticos, originalmente escrito pelo prof. Paulo Sérgio C. LinoVeja mais:
Valor absoluto e a desigualdade triangularA Astronomia e os astrônomos da Grécia Antiga
Teste da integral para convergência de séries

- Resolução Da Integral $\int \frac{1}{a-bx}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a-bx}dx = -\frac{\ln(a-bx)}{b}+C \end{equation*} onde $a$ e $b$ são constantes tais que $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq bx$ e $b \neq 0$. Seja a integral: \begin{equation*}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
