Matemática
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência.
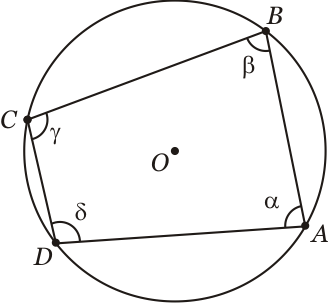
Por hipóteses temos que o quadrilátero $ABCD$ está inscrito na circunferência $\lambda$. Em tese temos que:
\begin{equation}
\left\{\begin{matrix}
\alpha & + & \gamma & = & 180^\circ\\
\beta & + & \delta & = & 180^\circ
\end{matrix}\right.
\end{equation}
\begin{equation}
\alpha=\frac{\widehat{BCD}}{2}
\end{equation}
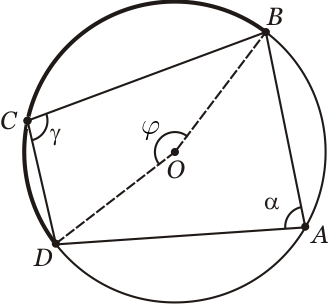
Analogamente temos que o ângulo $\gamma$ é igual à metade do arco $\widehat{DAB}$:
\begin{equation}
\gamma = \frac{\widehat{DAB}}{2}
\end{equation}
Assim:
\begin{equation}
\left.\begin{matrix}
\alpha & = & \frac{\widehat{BCD}}{2}\\
\gamma& = & \frac{\widehat{DAB}}{2}
\end{matrix}\right\}
\Rightarrow \alpha + \gamma = \frac{\widehat{BCD}+\widehat{DAB}}{2}=\frac{360^\circ}{2}=180^\circ
\end{equation}Analogamente provamos que $\beta + \delta = 180^\circ$, ou ainda observando que como a soma dos ângulos internos de uma quadrilátero é igual a $360^\circ$, segue que $\beta + \delta = 180^\circ$.
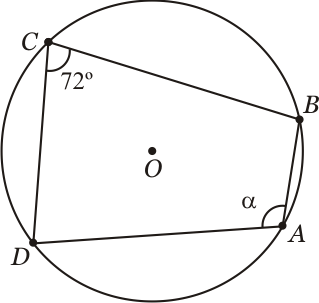
Sabemos que $\alpha + 72^\circ = 180^\circ$. Então $\alpha = 180^\circ - 72^\circ = 108^\circ$.
$b)$ Calcule o valor de $\alpha$:
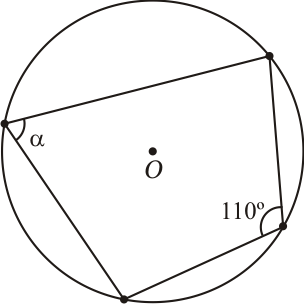
Como $\alpha + 110^\circ = 180^\circ$, então $\alpha = 180^\circ - 110^\circ = 70^\circ$.
$c)$ Calcule o valor de $\alpha$:
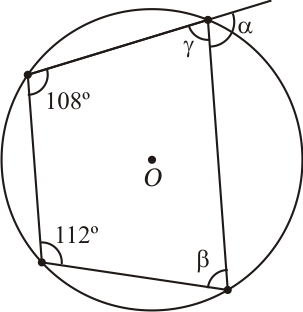
Sabemos que $112^\circ + \gamma = 180^\circ$. Então, $\gamma = 68^\circ$. Por outro lado, $\alpha + \gamma = 180^\circ$. Substituindo o valor de $\gamma$, obtemos: $\alpha = 180^\circ - 68^\circ = 112^\circ$.
➋ Teorema do Ângulo Inscrito
➌ Quadriláteros Notáveis

- Um Problema Famoso De Geometria
Olá gente! Hoje aprensentarei um problema bastante conhecido em geometria e algumas de suas soluções também muito conhecidas. O triângulo ao lado é isósceles de vértice . Sendo e calcule . Resolução 1 : Vamos usar lei dos senos...
- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Soma Dos Ângulos Internos E Externos De Um Polígono Convexo
A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$. Ângulos Internos Definição $1$: Ângulo interno...
- Os Pontos De Brocard (parte 2)
Na primeira postagem desta série, vimos as definições dos Pontos de Brocard e suas construções geométricas. Nesta postagem, veremos algumas propriedades importantes, teorema, corolários e suas respectivas demonstrações. Por: Kleber KilhianPaulo...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
Matemática
Teorema do Quadrilátero Inscritível
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência.

Teorema:
Se um quadrilátero é inscritível numa circunferência, então os ângulos opostos são suplementares.Por hipóteses temos que o quadrilátero $ABCD$ está inscrito na circunferência $\lambda$. Em tese temos que:
\begin{equation}
\left\{\begin{matrix}
\alpha & + & \gamma & = & 180^\circ\\
\beta & + & \delta & = & 180^\circ
\end{matrix}\right.
\end{equation}
Demonstração:
Pelo teorema do ângulo inscrito, temos que o ângulo $\alpha$ é igual à metade do arco $\widehat{BCD}$:\begin{equation}
\alpha=\frac{\widehat{BCD}}{2}
\end{equation}

Analogamente temos que o ângulo $\gamma$ é igual à metade do arco $\widehat{DAB}$:
\begin{equation}
\gamma = \frac{\widehat{DAB}}{2}
\end{equation}
Assim:
\begin{equation}
\left.\begin{matrix}
\alpha & = & \frac{\widehat{BCD}}{2}\\
\gamma& = & \frac{\widehat{DAB}}{2}
\end{matrix}\right\}
\Rightarrow \alpha + \gamma = \frac{\widehat{BCD}+\widehat{DAB}}{2}=\frac{360^\circ}{2}=180^\circ
\end{equation}Analogamente provamos que $\beta + \delta = 180^\circ$, ou ainda observando que como a soma dos ângulos internos de uma quadrilátero é igual a $360^\circ$, segue que $\beta + \delta = 180^\circ$.
Exemplos:
$a)$ Calcule o valor de $\alpha$:
Sabemos que $\alpha + 72^\circ = 180^\circ$. Então $\alpha = 180^\circ - 72^\circ = 108^\circ$.
$b)$ Calcule o valor de $\alpha$:

Como $\alpha + 110^\circ = 180^\circ$, então $\alpha = 180^\circ - 110^\circ = 70^\circ$.
$c)$ Calcule o valor de $\alpha$:

Sabemos que $112^\circ + \gamma = 180^\circ$. Então, $\gamma = 68^\circ$. Por outro lado, $\alpha + \gamma = 180^\circ$. Substituindo o valor de $\gamma$, obtemos: $\alpha = 180^\circ - 68^\circ = 112^\circ$.
Referências:
[1] Fundamentos de Matemática Elementar V9 - Geometria Plana - Osvaldo Dolce & Nicolau PompeoVeja mais:
➊ Organograma dos Quadriláteros Notáveis➋ Teorema do Ângulo Inscrito
➌ Quadriláteros Notáveis

- Um Problema Famoso De Geometria
Olá gente! Hoje aprensentarei um problema bastante conhecido em geometria e algumas de suas soluções também muito conhecidas. O triângulo ao lado é isósceles de vértice . Sendo e calcule . Resolução 1 : Vamos usar lei dos senos...
- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Soma Dos Ângulos Internos E Externos De Um Polígono Convexo
A soma dos ângulos internos de um polígono convexo depende da quantidade de lados que esse polígono possui; já a soma dos ângulos externos de um polígono convexo é uma constante e vale $360^\circ$. Ângulos Internos Definição $1$: Ângulo interno...
- Os Pontos De Brocard (parte 2)
Na primeira postagem desta série, vimos as definições dos Pontos de Brocard e suas construções geométricas. Nesta postagem, veremos algumas propriedades importantes, teorema, corolários e suas respectivas demonstrações. Por: Kleber KilhianPaulo...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
