Matemática
Hoje vamos aprender a resolver tipos específicos de equações: as da forma , nos reais positivos*
, nos reais positivos*
Primeiro, vamos trabalhar com a equação:


)x}%20x^a%20=%201)
}{a}%20x}%20x%20=%201)
}{a}%20x}%20(-%20\frac{(\ln{a})}{a}%20x)%20=%20-%20\frac{(\ln{a})}{a})
}{a}%20\iff%20y%20=%20W(%20-%20\frac{(\ln{a})}{a}))
}{a})}{\ln{a}})


%20\\%20x%20=%20e^{W(\ln{z})}%20=%20\frac{\ln{z}}{W(\ln{z})})
Primeiro, aplicando nosso "teorema", obtemos que todas as soluções são dadas por
}{\ln{2}})
}{\ln{2}})
- Questão 41 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Os pares ordenados (0, 0) e (1, 3) pertencem ao gráfico de uma função polinomial do 2.º grau. O máximo dessa função tem abscissa x = 2. Logo, o valor da função no ponto de abscissa x = ?1 é (A) 5.(B) 4.(C) 0.(D) ?4.(E) ?5. Solução: (E) Aplicando...
- Questão 27 ? Prova Do Estado ? (ofa) 2.011
Sendo x um número real, a equação: (?2x + 3) ? (x2 ? 2) ? (125 + x3) = 0 possui apenas: (A) três soluções racionais e nenhuma irracional.(B) três soluções irracionais e nenhuma racional.(C) duas soluções racionais e duas irracionais.(D)...
- Função Do 2º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equação
Equação Algébrica - Exercícios resolvidos 01. (VUNESP) Assinale a alternativa que indica o polinômio que possui os números 0 e 1 como raízes, sendo 0 uma raiz de multiplicidade 3: a) p(x) = x (x3 - 1) b) p(x) = x (x - 1)3 c) p(x) = x3 (x - 1)...
- Função Exponencial
Uma função f : dada pela lei f(x) = ax, onde a > 0 e a 1 é chamada de função exponencial.Se a > 1 a função é crescente ...
Matemática
Explorando equações exponencias através de Lambert
Hoje vamos aprender a resolver tipos específicos de equações: as da forma
Primeiro, vamos trabalhar com a equação:
Extraindo raíz a-ésima,
A partir deste momento, precisamos de uma nova definição:
Definição: A função W de Lambert é a relação inversa de %20=%20W%20e^W) . Reparem que, para certos valores de f(W), W não é uma função, mas sim uma relação - associa um elemento a dois distintos.
. Reparem que, para certos valores de f(W), W não é uma função, mas sim uma relação - associa um elemento a dois distintos.
Foi provado ser impossível escrevê-la em termos de funções matemáticas elementares. Porém, ela ainda é útil: na equação acima, podemos notar, chamando nosso expoente de y , que
Substituindo de volta, obtemos que todas as nossas soluções para a equação dada são dadas por
É muito interessante trabalhar também com a função  para descobrir quantas soluções tem certa equação em expoentes. Por exemplo,
para descobrir quantas soluções tem certa equação em expoentes. Por exemplo,
Exemplo 1: Ache todas as soluções de  .
.
Resolução: Extraindo logarítmo na base e dos dois lados,
Onde utilizamos, por vezes, as propriedades da definição da função W de Lambert.
Agora, vamos a um exemplo mais concreto: resolver  nos reais.
nos reais.
Primeiro, aplicando nosso "teorema", obtemos que todas as soluções são dadas por
Donde temos apenas que trabalhar com ) . Sabemos, porém, que
. Sabemos, porém, que
'%20=%20(1+x)e^x)
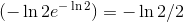
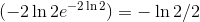



)
})
}%20\right%20)^2)
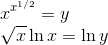
)
)
^2%20=%20\frac{1}{4})
^2%20=%20\frac{1}{16}%20\square)
Para a derivada ser igual a zero, e, portanto, termos um ponto crítico da função, temos de ter x = -1. Logo, toda equação tem 0,1 ou 2 soluções positivas. Como sabemos que
Então - ln 2 é um valor de W. Porém,
Logo, -2 ln 2 também é um valor possível de W. Como há no máximo duas positivas, há exatamente duas. Substituindo, obtemos x = 2 e x = 4, que são todas as soluções positivas da equação. 
Exemplo 2: (Revista Eureka!, número 35) Ache todas as soluções reais de  .
.
Resolução: Primeiro, tomemos ln em ambos os lados:
Aplicando a aplicação W,
Porém, sabemos que ) é igual a - ln 2 ou a - 2 ln 2.
é igual a - ln 2 ou a - 2 ln 2.
Lema: A função ) , quando analisamos sua intersecção com uma reta paralela ao eixo horizontal, pode no máximo gerar dois pontos.
, quando analisamos sua intersecção com uma reta paralela ao eixo horizontal, pode no máximo gerar dois pontos.
Demonstração: Calculemos a derivada de f:
Derivando implicitamente,
Como a função é definida apenas em reais positivos, é suficiente achar o x que zere ln x + 2. Isto é óbvio, a única solução é  . Portanto, como temos apenas um ponto de inflexão, há, no máximo, dois pontos de intersecção.
. Portanto, como temos apenas um ponto de inflexão, há, no máximo, dois pontos de intersecção. 
Agora, usando o Lema, as nossas duas soluções formam todo nosso conjunto solução, pois x é real positivo. Portanto,
- Questão 41 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Os pares ordenados (0, 0) e (1, 3) pertencem ao gráfico de uma função polinomial do 2.º grau. O máximo dessa função tem abscissa x = 2. Logo, o valor da função no ponto de abscissa x = ?1 é (A) 5.(B) 4.(C) 0.(D) ?4.(E) ?5. Solução: (E) Aplicando...
- Questão 27 ? Prova Do Estado ? (ofa) 2.011
Sendo x um número real, a equação: (?2x + 3) ? (x2 ? 2) ? (125 + x3) = 0 possui apenas: (A) três soluções racionais e nenhuma irracional.(B) três soluções irracionais e nenhuma racional.(C) duas soluções racionais e duas irracionais.(D)...
- Função Do 2º Grau
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
- Equação
Equação Algébrica - Exercícios resolvidos 01. (VUNESP) Assinale a alternativa que indica o polinômio que possui os números 0 e 1 como raízes, sendo 0 uma raiz de multiplicidade 3: a) p(x) = x (x3 - 1) b) p(x) = x (x - 1)3 c) p(x) = x3 (x - 1)...
- Função Exponencial
Uma função f : dada pela lei f(x) = ax, onde a > 0 e a 1 é chamada de função exponencial.Se a > 1 a função é crescente ...
