Matemática
Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence ao segundo conjunto dado.
Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6} consideremos a correspondência de A em B, de tal modo que cada elemento do conjunto A se associa no conjunto B com o seu sucessor. Assim ; ; . A correspondência por pares ordenados seria:
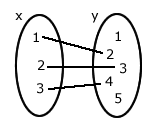
(2) Cada elemento de x tem um e somente um correspondente em y.
Logo, somente o diagrama 2 representa uma função.
Domínio, Contradomínio e Imagem
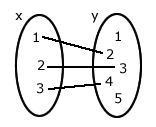
O conjunto X={1,2,3} denomina-se domínio da função f.
D(F)=X
O conjunto Y={1,2,3,4,5} denomina-se contradomínio da função f.
C(F)=Y
Dizemos que 2 é a imagem de 1 pela função f.
f(1)=2
Ainda, f(2)=3 e f(3)=4.
y = f(x) = x + 1
[Sol] f(1) = 1+1 = 2
f(2) = 2+1 = 3
f(3) =3+1 = 4
Logo: Im(f)={2,3,4}
b) D(f) = {1,3,5}
y = f(x) = x²
[Sol] f(1) = 1² = 1
f(3) = 3² = 9
f(5) = 5² = 25
Logo: Im(f)={1,9,25}
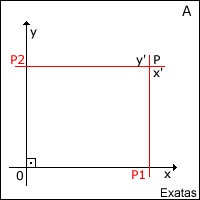Consideremos dois eixos x e y perpendiculares em 0, os quais determinam o plano A.
Denominemos P1 a interseção de x com y' e P2 a interseção de y com x'
- Ordenada de P é um número real representado por P2
- A coordenada de P são números reais x' e y' , geralmente indicados na forma de par ordenado ( x' , y' )
- O eixo das abscissas é o eixo x
- O eixo das ordenadas é o eixo y
- A origem do sistema é o ponto 0
- Plano cartesiano é o plano A.
- Conjunto
PAR ORDENADO : conjunto ordenado de dois elementos, representado pelo símbolo (x;y) onde x e y são números reais, denominados respectivamente de abscissa e ordenada. Ex: Par ordenado (6; -3) : abscissa = 6 e ordenada = -3.> Propriedade: dois pares...
- Conjunto
Plano Cartesiano O plano cartesiano é definido por dois eixos orientados x e y – as dimensões -, perpendiculares entre si, que se cruzam no ponto O, origem de ambos os eixos, conforme figura a seguir. Plano Cartesiano Observações: * O eixo x...
- Domínio, Contradomínio E Imagem De Uma Função
Domínio, Contradomínio e Imagem de uma Função Marcos Noé FunçãoUma função é dada por uma relação entre dois conjuntos, definida por uma lei de formação. Ao estudarmos uma função determinamos o domínio, o contradomínio...
- Domínio, Contradomínio E Imagem De Uma Função
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio...
- Função Do 1º Grau
Função do 1º grau Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence...
Matemática
Função
Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence ao segundo conjunto dado.
Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6} consideremos a correspondência de A em B, de tal modo que cada elemento do conjunto A se associa no conjunto B com o seu sucessor. Assim ; ; . A correspondência por pares ordenados seria:
Noções de função
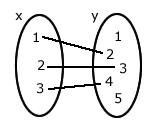
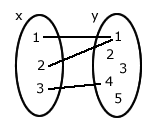
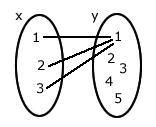
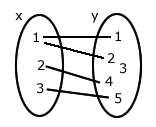
Considere os diagramas abaixo:
Condições de existência
(1) Todos os elementos de x têm um correspondente em y.(2) Cada elemento de x tem um e somente um correspondente em y.
Analisando os diagramas acima
O diagrama 1 não satisfaz a condição (1); os diagramas 3, 4 e 5 não satisfazem a condição (2).Logo, somente o diagrama 2 representa uma função.
Domínio, Contradomínio e Imagem
Observe o diagrama a seguir:
Chamemos esta função de f, logo o conjunto de pares ordenados serão:
f={(1,2),(2,3),(3,4)}O conjunto X={1,2,3} denomina-se domínio da função f.
D(F)=X
O conjunto Y={1,2,3,4,5} denomina-se contradomínio da função f.
C(F)=Y
Dizemos que 2 é a imagem de 1 pela função f.
f(1)=2
Ainda, f(2)=3 e f(3)=4.
Logo o conjunto das imagens de f e dado por:
Im(f)={2,3,4}Determinação de função
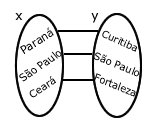
Observe:1) Associe cada elemento de X com o seu consecutivo:
2) Associe cada elemento de X com a sua capital
3) Determine o conjunto imagem de cada função:
a) D(f) = {1,2,3}y = f(x) = x + 1
[Sol] f(1) = 1+1 = 2
f(2) = 2+1 = 3
f(3) =3+1 = 4
Logo: Im(f)={2,3,4}
b) D(f) = {1,3,5}
y = f(x) = x²
[Sol] f(1) = 1² = 1
f(3) = 3² = 9
f(5) = 5² = 25
Logo: Im(f)={1,9,25}
Plano cartesiano
Dado um plano P qualquer, pertencente ao plano A, conduzamos por ele duas retas:
x // x' e y // y'Denominemos P1 a interseção de x com y' e P2 a interseção de y com x'
Nessas condições, definimos:
- Abscissa de P é um número real representado por P1- Ordenada de P é um número real representado por P2
- A coordenada de P são números reais x' e y' , geralmente indicados na forma de par ordenado ( x' , y' )
- O eixo das abscissas é o eixo x
- O eixo das ordenadas é o eixo y
- A origem do sistema é o ponto 0
- Plano cartesiano é o plano A.
- Conjunto
PAR ORDENADO : conjunto ordenado de dois elementos, representado pelo símbolo (x;y) onde x e y são números reais, denominados respectivamente de abscissa e ordenada. Ex: Par ordenado (6; -3) : abscissa = 6 e ordenada = -3.> Propriedade: dois pares...
- Conjunto
Plano Cartesiano O plano cartesiano é definido por dois eixos orientados x e y – as dimensões -, perpendiculares entre si, que se cruzam no ponto O, origem de ambos os eixos, conforme figura a seguir. Plano Cartesiano Observações: * O eixo x...
- Domínio, Contradomínio E Imagem De Uma Função
Domínio, Contradomínio e Imagem de uma Função Marcos Noé FunçãoUma função é dada por uma relação entre dois conjuntos, definida por uma lei de formação. Ao estudarmos uma função determinamos o domínio, o contradomínio...
- Domínio, Contradomínio E Imagem De Uma Função
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio...
- Função Do 1º Grau
Função do 1º grau Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence...