Matemática

Plano Cartesiano
O plano cartesiano é definido por dois eixos orientados x e y – as dimensões -, perpendiculares entre si, que se cruzam no ponto O, origem de ambos os eixos, conforme figura a seguir.
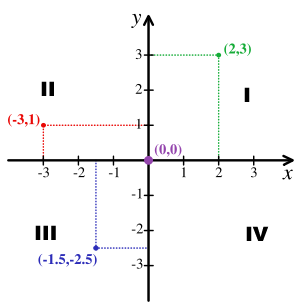
Plano Cartesiano
Observações:
* O eixo x é denominado de eixo das abcissas ou eixo Ox;
* O eixo y é denominado de eixo das ordenadas ou eixo Oy;
* Os dois eixos dividem o plano em quatro quadrantes (I, II, III e IV na figura);
* Cada ponto P do plano cartesiano é identificado por dois números reais x e y e é representado na forma de um par ordenado (x,y), também chamado de coordenadas do ponto P, onde x é a abcissa e y a ordenada;
* Um ponto P é obtido por meio do encontro das perpendiculares aos eixos Ox e Oy traçadas a partir de sua abcissa e de sua ordenada. Veja na figura a representação do ponto P = (2,3);
* A origem O é representada pelo par ordenado (0,0);
* Os pontos do quadrante I são representados pelos pares ordenados (x,y) em que x e y são positivos;
* E os do quadrante II pelos pares ordenados (x,y) em que x < 0 e y > 0;
* Os do quadrante III pelos pares ordenados (x,y) em que x e y são negativos;
* Os pontos do quadrante IV são representados pelos pares ordenados (x,y) em que x > 0 e y < 0; * Um par ordenado (a,b) é igual a outro par ordenado (c,d) se, e somente se, a = c e b = d; * Em um par ordenado (a,b), se a é diferente de b, então (a,b) é diferente do par ordenado (b,a). Determine, por exemplo, no plano cartesiano os pontos P = (1,2) e Q = (2,1) para comprovar a afirmação; * De forma resumida, podemos afirmar que, no plano cartesiano, cada ponto é representado por um único par ordenado (a,b), a e b números reais. A recíproca também é verdadeira, ou seja, cada par ordenado (a,b) representa um único ponto no plano cartesiano; * E, por fim, o plano cartesiano é obtido associando-se a cada um dos eixos o conjunto dos números reais. Produto Cartesiano Sejam A e B dois conjuntos não vazios. Definimos como produto cartesiano de A por B o conjunto A x B cujos elementos são todos os pares ordenados (a,b) em que a pertence a A e b pertence a B: A x B = {(a,b) | a Ɛ A e b Ɛ B} Observações: * O símbolo A x B lê-se “A cartesiano B” ou “produto cartesiano de A por B”; * Se o conjunto A é diferente do conjunto B, A e B diferentes do conjunto vazio, então A x B é diferente de B x A, veja exemplo abaixo; * A x ø = ø, ø x A = ø e ø x ø = ø; * Se A ou B é infinito e nenhum deles for vazio, então A x B é infinito; * A x A pode ser também representado por A2, que se lê “A dois”; * Se A e B são finitos e A tem m elementos e B tem n elementos, então A x B tem m.n elementos: n(A x B) = n(A).n(B) = m.n. Exemplo extraído do livro Fundamentos de Matemática Elementar, Vol 01, Conjuntos e Funções – ver referências no final do post: Se A = {1,2,3} e B = {1,2} então: A x B = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)} e B x A = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)} cujas representações no plano cartesiano são as seguintes: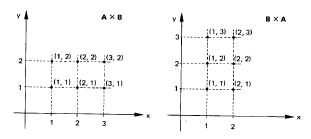
Exemplo de Produto Cartesiano - Gráficos
Relação Binária
Dados dois conjunto A e B não vazios, chama-se relação R, ou mais simplesmente relação binária, de A em B a qualquer subconjunto de A x B. Uma relação R de A em B é representada pelo símbolo R: A -> B:
R: A -> B <=> R C A x B
Exemplo:
Se A = {1,5} e B = {3,4,6}, então A x B = {(1,3), (1,4), (1,6), (5,3), (5,4), (5,6)}. Logo:
R = {(1,3), (1,6), (5,4)}
S = {(5.4)}
T = {(1,3), (1,4), (5,3), (5,6)}
são relações de A em B, uma vez que R, S e T são subconjuntos de A x B.
As relações que estabelecem uma condição matemática para que um determinado par ordenado (x,y) pertença à uma relação são de grande importância. Vejamos alguns exemplos para ilustrar o fato.
Se A = {1,3,4} e B = {2,4}, então A x B = {(1,2), (1,4), (3,2), (3,4), (4,2), (4,4)}. São relações de A em B:
a) R = {(x,y) Ɛ A x B | x = y} = {(4,4)}
b) S = {(x,y) Ɛ A x B | x/y Ɛ Z} = {(4,2), (4,4)}
c) T = {(x,y) Ɛ A x B | y – x = 1} = {(1,2), (3,4)}
Domínio e Imagem
Seja R uma relação de A em B.
1. Chama-se domínio de R, e denotamos por D(R), o conjunto de todos os primeiros elementos dos pares ordenados pertencentes a R. Ou, alternativamente, o conjunto de todos os elementos de A que estão associados a pelo menos um elemento de B.
2. Chama-se imagem de R, e denotamos por Im(R), o conjunto de todos os segundos elementos dos pares ordenados pertencentes a R.
Com base no exemplo anterior, temos:
a) D(R) = {4} e Im(R) = {4}
b) D(S) = {4} e Im(S) = {2,4}
c) D(T) = {1,3} e Im(T) = {2,4}
Referências
1. Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
2. Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001.
- Introdução à Geometria Analítica
Para começar o estudo da geometria analítica, é necessário conhecer o Plano Cartesiano: O Eixo Y (linha vertical) é chamado de eixo das ordenadas, enquanto que o Eixo X (linha horizontal), é chamado de eixo das abscissas. O ponto P (ponto vermelho...
- Relação
Relação Aqui iremos trabalhar a relação entre dois conjuntos e as formas pelas quais essa relação pode ser representada. Dado dois conjuntos A = {0, 1, 2, 3} e B = {3, 4, 5, 6}, atribuímos à relação de A para B (A → B), isso significa que...
- Função
Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence ao segundo conjunto dado. Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6} consideremos a correspondência...
- Produto Cartesiano
Um par ordenado é formado pelos valores de x e y agrupados, os quais determinam pontos no plano cartesiano. A coordenada (x, y) indica que os valores de x estão atribuídos à abscissa (eixo x) e os valores de y à ordenada (eixo y). Produto cartesiano...
- Plano Cartesiano
O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano, foi criado por René Descartes com o objetivo de localizar pontos. Ele é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas....
Matemática
Conjunto

Plano Cartesiano
O plano cartesiano é definido por dois eixos orientados x e y – as dimensões -, perpendiculares entre si, que se cruzam no ponto O, origem de ambos os eixos, conforme figura a seguir.

Plano Cartesiano
Observações:
* O eixo x é denominado de eixo das abcissas ou eixo Ox;
* O eixo y é denominado de eixo das ordenadas ou eixo Oy;
* Os dois eixos dividem o plano em quatro quadrantes (I, II, III e IV na figura);
* Cada ponto P do plano cartesiano é identificado por dois números reais x e y e é representado na forma de um par ordenado (x,y), também chamado de coordenadas do ponto P, onde x é a abcissa e y a ordenada;
* Um ponto P é obtido por meio do encontro das perpendiculares aos eixos Ox e Oy traçadas a partir de sua abcissa e de sua ordenada. Veja na figura a representação do ponto P = (2,3);
* A origem O é representada pelo par ordenado (0,0);
* Os pontos do quadrante I são representados pelos pares ordenados (x,y) em que x e y são positivos;
* E os do quadrante II pelos pares ordenados (x,y) em que x < 0 e y > 0;
* Os do quadrante III pelos pares ordenados (x,y) em que x e y são negativos;
* Os pontos do quadrante IV são representados pelos pares ordenados (x,y) em que x > 0 e y < 0; * Um par ordenado (a,b) é igual a outro par ordenado (c,d) se, e somente se, a = c e b = d; * Em um par ordenado (a,b), se a é diferente de b, então (a,b) é diferente do par ordenado (b,a). Determine, por exemplo, no plano cartesiano os pontos P = (1,2) e Q = (2,1) para comprovar a afirmação; * De forma resumida, podemos afirmar que, no plano cartesiano, cada ponto é representado por um único par ordenado (a,b), a e b números reais. A recíproca também é verdadeira, ou seja, cada par ordenado (a,b) representa um único ponto no plano cartesiano; * E, por fim, o plano cartesiano é obtido associando-se a cada um dos eixos o conjunto dos números reais. Produto Cartesiano Sejam A e B dois conjuntos não vazios. Definimos como produto cartesiano de A por B o conjunto A x B cujos elementos são todos os pares ordenados (a,b) em que a pertence a A e b pertence a B: A x B = {(a,b) | a Ɛ A e b Ɛ B} Observações: * O símbolo A x B lê-se “A cartesiano B” ou “produto cartesiano de A por B”; * Se o conjunto A é diferente do conjunto B, A e B diferentes do conjunto vazio, então A x B é diferente de B x A, veja exemplo abaixo; * A x ø = ø, ø x A = ø e ø x ø = ø; * Se A ou B é infinito e nenhum deles for vazio, então A x B é infinito; * A x A pode ser também representado por A2, que se lê “A dois”; * Se A e B são finitos e A tem m elementos e B tem n elementos, então A x B tem m.n elementos: n(A x B) = n(A).n(B) = m.n. Exemplo extraído do livro Fundamentos de Matemática Elementar, Vol 01, Conjuntos e Funções – ver referências no final do post: Se A = {1,2,3} e B = {1,2} então: A x B = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)} e B x A = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)} cujas representações no plano cartesiano são as seguintes:

Exemplo de Produto Cartesiano - Gráficos
Relação Binária
Dados dois conjunto A e B não vazios, chama-se relação R, ou mais simplesmente relação binária, de A em B a qualquer subconjunto de A x B. Uma relação R de A em B é representada pelo símbolo R: A -> B:
R: A -> B <=> R C A x B
Exemplo:
Se A = {1,5} e B = {3,4,6}, então A x B = {(1,3), (1,4), (1,6), (5,3), (5,4), (5,6)}. Logo:
R = {(1,3), (1,6), (5,4)}
S = {(5.4)}
T = {(1,3), (1,4), (5,3), (5,6)}
são relações de A em B, uma vez que R, S e T são subconjuntos de A x B.
As relações que estabelecem uma condição matemática para que um determinado par ordenado (x,y) pertença à uma relação são de grande importância. Vejamos alguns exemplos para ilustrar o fato.
Se A = {1,3,4} e B = {2,4}, então A x B = {(1,2), (1,4), (3,2), (3,4), (4,2), (4,4)}. São relações de A em B:
a) R = {(x,y) Ɛ A x B | x = y} = {(4,4)}
b) S = {(x,y) Ɛ A x B | x/y Ɛ Z} = {(4,2), (4,4)}
c) T = {(x,y) Ɛ A x B | y – x = 1} = {(1,2), (3,4)}
Domínio e Imagem
Seja R uma relação de A em B.
1. Chama-se domínio de R, e denotamos por D(R), o conjunto de todos os primeiros elementos dos pares ordenados pertencentes a R. Ou, alternativamente, o conjunto de todos os elementos de A que estão associados a pelo menos um elemento de B.
2. Chama-se imagem de R, e denotamos por Im(R), o conjunto de todos os segundos elementos dos pares ordenados pertencentes a R.
Com base no exemplo anterior, temos:
a) D(R) = {4} e Im(R) = {4}
b) D(S) = {4} e Im(S) = {2,4}
c) D(T) = {1,3} e Im(T) = {2,4}
Referências
1. Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
2. Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001.
- Introdução à Geometria Analítica
Para começar o estudo da geometria analítica, é necessário conhecer o Plano Cartesiano: O Eixo Y (linha vertical) é chamado de eixo das ordenadas, enquanto que o Eixo X (linha horizontal), é chamado de eixo das abscissas. O ponto P (ponto vermelho...
- Relação
Relação Aqui iremos trabalhar a relação entre dois conjuntos e as formas pelas quais essa relação pode ser representada. Dado dois conjuntos A = {0, 1, 2, 3} e B = {3, 4, 5, 6}, atribuímos à relação de A para B (A → B), isso significa que...
- Função
Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro conjunto dado e o segundo elemento pertence ao segundo conjunto dado. Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6} consideremos a correspondência...
- Produto Cartesiano
Um par ordenado é formado pelos valores de x e y agrupados, os quais determinam pontos no plano cartesiano. A coordenada (x, y) indica que os valores de x estão atribuídos à abscissa (eixo x) e os valores de y à ordenada (eixo y). Produto cartesiano...
- Plano Cartesiano
O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano, foi criado por René Descartes com o objetivo de localizar pontos. Ele é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas....
