Matemática
Nessa situação, temos que:
Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: representada pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
O conjunto domínio possui algumas características especiais que definem ou não uma função. Observe:
Todos os elementos do conjunto domínio devem possuir representação no conjunto do contradomínio. Caso isso não ocorra, a lei de formação não pode ser uma função.
Função
Não é uma função
Um único elemento do domínio não deve possuir duas imagens.
Não é função
Dois elementos diferentes do domínio podem possuir a mesma imagem.
Não é Função

Restam elementos no conjunto domínio, que não foram associados ao conjunto imagem.
mundoeducacao.com.br
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Propriedades De Uma Função
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação. Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características...
- Função
FunçãoDados dois conjuntos A e B não vazios, função é uma relação R de A em B se e somente se para todo elemento x de A existe um único correspondente y em B. Se você observar a figura ao lado esquerdo, verá que o elemento 1 de A possui a imagem...
- Propriedades De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
Matemática
Domínio, Contradomínio e Imagem de uma Função
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio e imagem. Essas características podem ser representadas por um diagrama de flechas, isso facilitará o entendimento por parte do estudante. Observe:
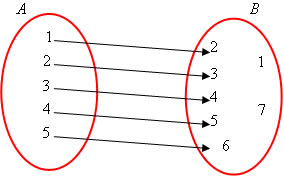
Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama de flechas:
Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama de flechas:

A | B |
x | f(X) |
1 | 2 |
2 | 3 |
3 | 4 |
4 | 5 |
5 | 6 |
Nessa situação, temos que:
Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: representada pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
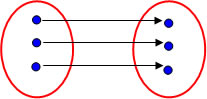
O conjunto domínio possui algumas características especiais que definem ou não uma função. Observe:
Todos os elementos do conjunto domínio devem possuir representação no conjunto do contradomínio. Caso isso não ocorra, a lei de formação não pode ser uma função.
Função

Não é uma função

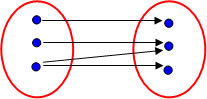
Um único elemento do domínio não deve possuir duas imagens.
Não é função

Dois elementos diferentes do domínio podem possuir a mesma imagem.
Não é Função

Restam elementos no conjunto domínio, que não foram associados ao conjunto imagem.
mundoeducacao.com.br
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Propriedades De Uma Função
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação. Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características...
- Função
FunçãoDados dois conjuntos A e B não vazios, função é uma relação R de A em B se e somente se para todo elemento x de A existe um único correspondente y em B. Se você observar a figura ao lado esquerdo, verá que o elemento 1 de A possui a imagem...
- Propriedades De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
