Função

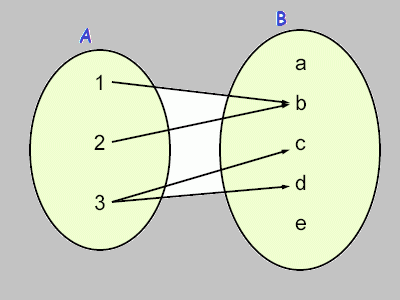
Dados dois conjuntos A e B não vazios, função é uma relação R de A em B se e somente se para todo elemento x de A existe um único correspondente y em B.

Se você observar a figura ao lado esquerdo, verá que o elemento 1 de A possui a imagem b em B, o elemento 2 de A possui imagem b em B, porém o elemento 3 de A possui as imagens c e d em B.

Então, concluímos que essa relação R de A em B não é uma função.

Exemplos de Funções:

Sejam os conjuntos A= {1,2,3} e B= {1,2,3,4,9} e as relações:
a) R1

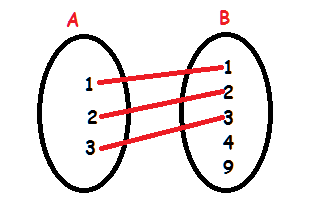
» R1 é uma função de A em B, pois todo elemento de A tem um único correspondente (imagem) em B

b) R2

» R2 é uma função de A em B, pois todo elemento de A tem uma única imagem em B
A imagem do 1€A é 1 em B.
A imagem do 2€A é 1 em B.
A imagem do 3€A é 4 em B.

Observação: Para que seja função:
1. Todo elemento de A tem imagem em B;
2. Cada elemento de A só tem uma única imagem em B.

Contra-exemplos:
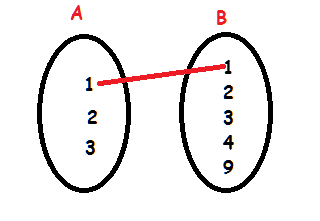
c) R3

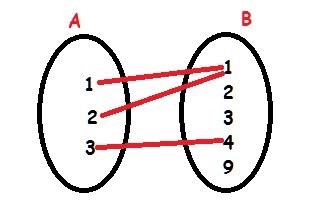
» R3 não é uma função, pois os elementos 2 e 3 de A não têm imagens em B.

d) R4

» R4 não é uma função, pois há elementos de A, o 1, com mais de uma imagem em B (1 de A, tem as imagens 1 e 2 em B).

Exercícios:

1. Dados os conjuntos: E= {1,2,3,4} e B={2,5,6} e as relações abaixo, escreva se é função ou não é função:
a) R1= {(1,2),(2,5),(3,6)}
b) R2= {(1,2),(2,5),(3,2),(4,6)}
c) R3= {(1,5),(2,5), (3,5),(4,5)}
d) R4= {(2,2),(3,5),(4,6)}

Respostas:
a) Veja: 1→2, 2→5, 3→6, como todos os elementos da esquerda (CONJUNTO E) têm uma única imagem, mas o 4 de E não têm imgem, logo: NÃO É FUNÇÃO.

b) Veja: 1→2, 2→5, 3→2 e 4→6, TODOS ELEMENTOS DE E TÊM IMAGENS - É FUNÇÃO.

c) Veja esquema: 1→5, 2→5, 3→5 e 4→5, idem - É FUNÇÃO.

d) Veja esquema: 2→2, 3→5, 4→6, Como o elemento 1 não tem imagem, NÃO É FUNÇÃO.

2. Dada a função f de A em B pelo diagrama de setas, dê a imagem dos elementos a, b, c, e d.

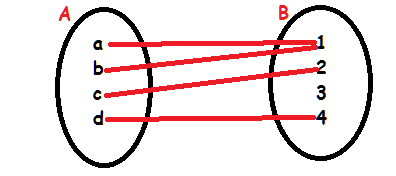
Resposta: Imagens de {a,b,c,d} são:{1,1,2,4}

Notação
Uma função f de A em B, ou seja, domínio em A e imagem no contradomínio B, indica-se:
f: A→B (lê-se f de A em B)
Assim, cada elemento x de A está associado a um único y, imagem de x pela função f, que se indica f(x) e lê-se f de x.

RESUMO:
» O conjunto A chama-se domínio da função f.
» O conjunto B chama-se contradomínio da função f.
» x é o elemento arbitrário do domínio.
» y=f(x) é a imagem de x no contradomínio.
» O conjunto dos elementos de B que são imagens dos elementos de A forma o conjunto imagem (Im).

fonte:recordandomatematica.blogspot.com.br