Matemática
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação.
Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características em uma função é preciso que tenhamos o conhecimento da definição de função, do que é um domínio, imagem e contradomínio.
Observe o diagrama abaixo que representa uma função f: A→B e veja quem é o domínio, a imagem e o contradomínio dela.
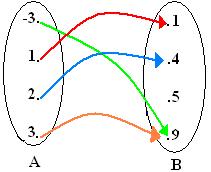
Domínio serão todos os elementos do conjunto A: D(f) = {-3,1,2,3} a imagem será os elementos do conjunto B que receberem a seta: Im(f) = {1,4,9} e o contradomínio será todos os elementos do conjunto B: CD(f) = {1,4,5,9}.
Agora, veja como identificar essas características da função:
Função sobrejetora
Uma função será sobrejetora se o conjunto imagem for igual ao conjunto do contradomínio, ou seja, o conjunto imagem será todos os elementos do conjunto de chegada. Matematicamente, podemos dizer que: f: A →B definida por uma fórmula qualquer será sobrejetora se Im(f) = B.
Função injetora
Uma função será injetora se os elementos do conjunto do domínio estiverem ligados a imagens distintas. Matematicamente podemos dizer que: f: A → B definida por uma fórmula qualquer será injetora se todos os elementos de A forem distintos (diferentes) e as imagens desses elementos forem distintas também.
Função bijerora
Para que uma função assuma a característica de uma função bijetora ela tem que ser ao mesmo tempo sobrejetora e injetora. O conjunto imagem deverá ser igual ao conjunto do contradomínio e todos os elementos do domínio deverão estar ligados a imagens distintas.
Danielle de Miranda
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Domínio, Contradomínio E Imagem De Uma Função
Domínio, Contradomínio e Imagem de uma Função Marcos Noé FunçãoUma função é dada por uma relação entre dois conjuntos, definida por uma lei de formação. Ao estudarmos uma função determinamos o domínio, o contradomínio...
- Funções Injetoras,bijetoras E Sobrejetoras
Aplicação Como a variável x está sob radical de índice par e tambem no denominador da fração: Funções sobrejetora, injetores e bijetora 1.º Tipo - sobrejetora f é sobrejetora Im (f) = CD (f) A Função é sobrejetora se sua imagem for igual...
- Tipos De Funções
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Domínio, Contradomínio E Imagem De Uma Função
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio...
Matemática
Propriedades de uma Função
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação.
Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características em uma função é preciso que tenhamos o conhecimento da definição de função, do que é um domínio, imagem e contradomínio.
Observe o diagrama abaixo que representa uma função f: A→B e veja quem é o domínio, a imagem e o contradomínio dela.
Domínio serão todos os elementos do conjunto A: D(f) = {-3,1,2,3} a imagem será os elementos do conjunto B que receberem a seta: Im(f) = {1,4,9} e o contradomínio será todos os elementos do conjunto B: CD(f) = {1,4,5,9}.
Agora, veja como identificar essas características da função:
Função sobrejetora
Uma função será sobrejetora se o conjunto imagem for igual ao conjunto do contradomínio, ou seja, o conjunto imagem será todos os elementos do conjunto de chegada. Matematicamente, podemos dizer que: f: A →B definida por uma fórmula qualquer será sobrejetora se Im(f) = B.
Função injetora
Uma função será injetora se os elementos do conjunto do domínio estiverem ligados a imagens distintas. Matematicamente podemos dizer que: f: A → B definida por uma fórmula qualquer será injetora se todos os elementos de A forem distintos (diferentes) e as imagens desses elementos forem distintas também.
Função bijerora
Para que uma função assuma a característica de uma função bijetora ela tem que ser ao mesmo tempo sobrejetora e injetora. O conjunto imagem deverá ser igual ao conjunto do contradomínio e todos os elementos do domínio deverão estar ligados a imagens distintas.
Danielle de Miranda
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Domínio, Contradomínio E Imagem De Uma Função
Domínio, Contradomínio e Imagem de uma Função Marcos Noé FunçãoUma função é dada por uma relação entre dois conjuntos, definida por uma lei de formação. Ao estudarmos uma função determinamos o domínio, o contradomínio...
- Funções Injetoras,bijetoras E Sobrejetoras
Aplicação Como a variável x está sob radical de índice par e tambem no denominador da fração: Funções sobrejetora, injetores e bijetora 1.º Tipo - sobrejetora f é sobrejetora Im (f) = CD (f) A Função é sobrejetora se sua imagem for igual...
- Tipos De Funções
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Domínio, Contradomínio E Imagem De Uma Função
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio...
